- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

算法面试高频题解指南【一】

Ustinian_2022 发表于 2022/08/06 21:09:28 2022/08/06

【摘要】 👩‍💻博客主页：choice~的博客主页✨欢迎关注🖱点赞🎀收藏⭐留言✒🔮本文由choice~原创，csdn首发！👕参考网站：牛客网💻首发时间：🎞2022年7月22日🎠🎨你的收入跟你的不可替代成正比🀄如果觉得博主的文章还不错的话，请三连支持一下博主哦💬给大家介绍一个求职刷题收割offer的地方👉点击进入网站目录 1.NC110 旋转数组描述：探讨：算法思想一：使用...

👩‍💻博客主页：choice~的博客主页

✨欢迎关注🖱点赞🎀收藏⭐留言✒

🔮本文由choice~原创，csdn首发！

👕参考网站：牛客网

💻首发时间：🎞2022年7月22日🎠

🎨你的收入跟你的不可替代成正比

🀄如果觉得博主的文章还不错的话，请三连支持一下博主哦
💬给大家介绍一个求职刷题收割offer的地方👉点击进入网站

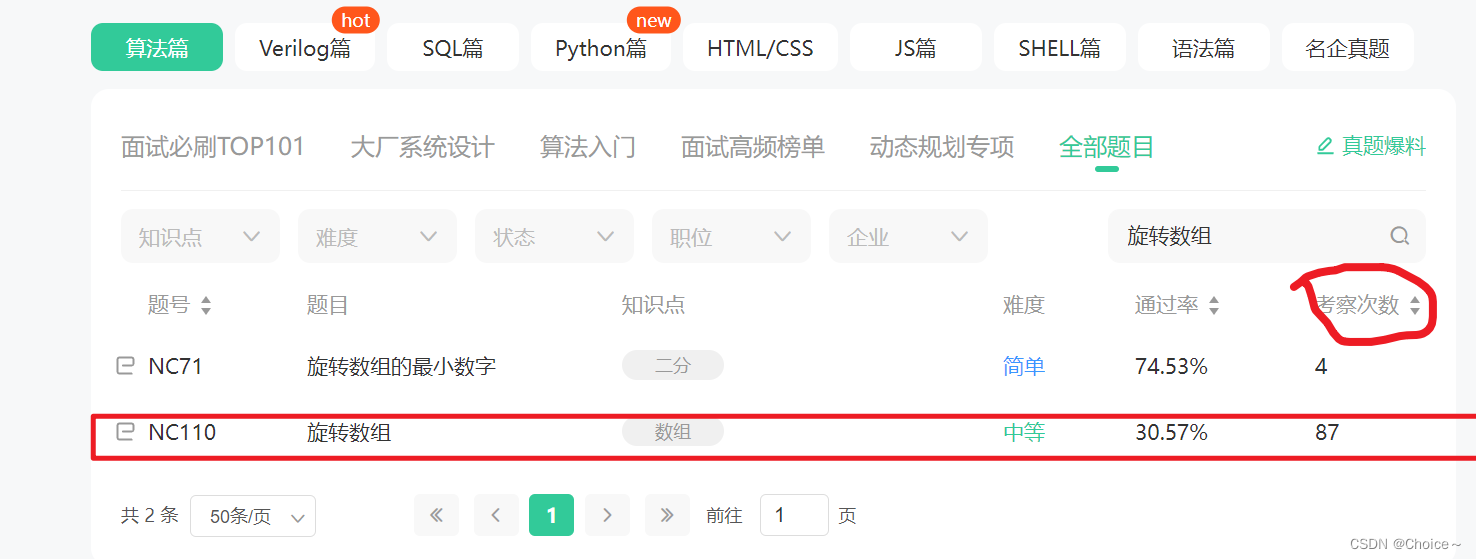
1.NC110 旋转数组

描述：

一个数组A中存有 n 个整数，在不允许使用另外数组的前提下，将每个整数循环向右移 M（ M >=0）个位置，即将A中的数据由（A0 A1 ……AN-1 ）变换为（AN-M …… AN-1 A0 A1 ……AN-M-1 ）（最后 M 个数循环移至最前面的 M 个位置）。如果需要考虑程序移动数据的次数尽量少，要如何设计移动的方法？

数据范围：0 < n \le 1000<n≤100，0 \le m \le 10000≤m≤1000

进阶：空间复杂度 O(1)O(1)，时间复杂度 O(n)O(n)

编辑

这是C语言给的OJ模块：

/**
 * 旋转数组
 * @param n int整型 数组长度
 * @param m int整型 右移距离
 * @param a int整型一维数组 给定数组
 * @param aLen int a数组长度
 * @return int整型一维数组
 * @return int* returnSize 返回数组行数
 */
int* solve(int n, int m, int* a, int aLen, int* returnSize ) {

}

探讨：

这道题呢是牛客网的面试高频榜单题NC110 旋转数组，中等级别,关联的企业和关联职位都要这道题，大家可以拿着这道题好好刷。

编辑

分析一下这道题的出现概率是非常大的居然考察数高达87次，这是多么庞大的数字啊，难度也是中等一般，（看下图）通过率也是偏低的；我们知道了为什么我拿这道题讲解的原因了吧！所以很有必要看看

编辑

题目主要信息:

一个长度为nnn的数组，将数组整体循环右移mmm个位置（mmm可能大于nnn）

循环右移即最后mmm个元素放在数组最前面，前n−mn-mn−m个元素依次后移

不能使用额外的数组空间

算法思想一：使用额外数组

解题思路：

可以使用额外的数组来将每个元素放至正确的位置。遍历原数组，将原数组下标为 i 的元素放至新数组下标为 (i+m) mod n （为了防止右移的长度大于数组的长度，所以才有取余）的位置，最后返回新数组即可

图解：编辑

代码展示：

JAVA版本

import java.util.*;

public class Solution {

/**

* 旋转数组

* @param n int整型数组长度

* @param m int整型右移距离

* @param a int整型一维数组给定数组

* @return int整型一维数组

*/

public int[] solve (int n, int m, int[] a) {

// write code here

// 额外新数组

int[] newArr = new int[n];

// 遍历原数组

for (int i = 0; i < n; ++i) {

// 数组元素旋转

newArr[(i + m) % n] = a[i];

}

return newArr;

}

复杂度分析

时间复杂度 O(n)：其中 n 为数组的长度，遍历数组时间O(n)

空间复杂度O(n)：额外新数组占用空间

算法思想二：数组翻转

解题思路：

该方法基于如下的事实：将数组的元素向右移动 k 次后，尾部 m mod n 个元素会移动至数组头部，其余元素向后移动 m mod n 个位置。
该方法为数组的翻转：翻转算法参考反转链表中的双指针方法题解 | #反转链表#_牛客博客

1、可以先将所有元素翻转，这样尾部的 m mod n 个元素就被移至数组头部，

2、然后再翻转 [0,m mod n−1] 区间的元素

3、最后翻转[m mod n,n−1] 区间的元素即能得到最后的答案。

实例：
以 n=7，m=3 为例进行如下展示：

操作	结果
原始数据	【1，2，3，4，5，6，7】
翻转所有元素	【7，6，5，4，3，2，1】
翻转 [0,m mod n −1] 区间的元素	【5，6，7，4，3，2，1】
翻转 [m mod n, n −1] 区间的元素	【5，6，7，1，2，3，4】

最后返回：【5，6，7，1，2，3，4】

代码展示：

Python版本

class Solution:

def solve(self , n , m , a ):

# write code here

m = m % n

# 数组反转

# 翻转全部

self.reverse(a, 0, n - 1);

# 再翻转【0，m-1】

self.reverse(a, 0, m - 1);

# 再翻转【m，n-1】

self.reverse(a, m, n - 1);

return a

def reverse(self, nums, start, end):

# 数组翻转

while start < end :

# 双指针遍历翻转

temp = nums[start];

nums[start] = nums[end];

nums[end] = temp;

start += 1;

end -= 1;

复杂度分析

时间复杂度：O(N)，其中 N 为数组的长度。每个元素被翻转两次，一共 N 个元素，因此总时间复杂度为 O(2N)=O(N)。
空间复杂度：O(1)。使用常数级空间变量

算法思想三：数组变换

解题思路：

简单便利的方法：数组直接变换

1、tmp = m mod n，找到右移的距离

2、采用 a[:tmp], a[tmp:] = a[-tmp:],a[:n-tmp] 直接变换

代码展示：

Python版本

class Solution:

def solve(self , n , m , a ):

# write code here

# 获取移动的距离

tmp = m % n

# 交换移动数组

a[:tmp], a[tmp:] = a[-tmp:],a[:n-tmp]

return a

复杂度分析

时间复杂度：O(n)，其中 n 为数组的长度。一共移动n个元素
空间复杂度：O(1)。使用常数级空间变量

举一反三：

学习完本题的思路你可以解决如下题目：

BM99. 顺时针旋转矩阵

方法：三次翻转（推荐使用）

思路：

循环右移相当于从第mmm个位置开始，左右两部分视作整体翻转。即abcdefg右移3位efgabcd可以看成AB翻转成BA（这里小写字母看成数组元素，大写字母看成整体）。既然是翻转我们就可以用到reverse函数。

具体做法:

step 1：因为mmm可能大于nnn，因此需要对nnn取余，因为每次长度为nnn的旋转数组相当于没有变化。
step 2：第一次将整个数组翻转，得到数组的逆序，它已经满足了右移的整体出现在了左边。
step 3：第二次就将左边的mmm个元素单独翻转，因为它虽然移到了左边，但是逆序了。
step 4：第三次就将右边的n−mn-mn−m个元素单独翻转，因此这部分也逆序了。

图示：编辑

Java代码实现:

public class Solution {

public int[] solve (int n, int m, int[] a) {

//取余，因为每次长度为n的旋转数组相当于没有变化

m = m % n;

//第一次逆转全部数组元素

reverse(a, 0, n - 1);

//第二次只逆转开头m个

reverse(a, 0, m - 1);

//第三次只逆转结尾m个

reverse(a, m, n - 1);

return a;

}

//反转函数

public void reverse(int[] nums, int start, int end){

while(start < end){

swap(nums, start++, end--);

}

//交换函数

public void swap(int[] nums, int a, int b){

int temp = nums[a];

nums[a] = nums[b];

nums[b] = temp;

}

C++代码实现:

class Solution {

public:

vector<int> solve(int n, int m, vector<int>& a) {

//取余，因为每次长度为n的旋转数组相当于没有变化

m = m % n;

//第一次逆转全部数组元素

reverse(a.begin(), a.end());

//第二次只逆转开头m个

reverse(a.begin(), a.begin() + m);

//第三次只逆转结尾m个

reverse(a.begin() + m, a.end());

return a;

}

};

Python实现代码：

class Solution:

def solve(self , n: int, m: int, a: List[int]) -> List[int]:

#取余，因为每次长度为n的旋转数组相当于没有变化

m = m % n

#第一次逆转全部数组元素

a.reverse()

b = a[:m]

#第二次只逆转开头m个

b.reverse()

c = a[m:]

#第三次只逆转结尾m个

c.reverse()

a[:m] = b

a[m:] = c

return a

复杂度分析：

时间复杂度：O(n)O(n)O(n)，三次reverse函数的复杂度都最坏为O(n)O(n)O(n)
空间复杂度：O(1)O(1)O(1)，没有使用额外的辅助空间

接下来再来一道

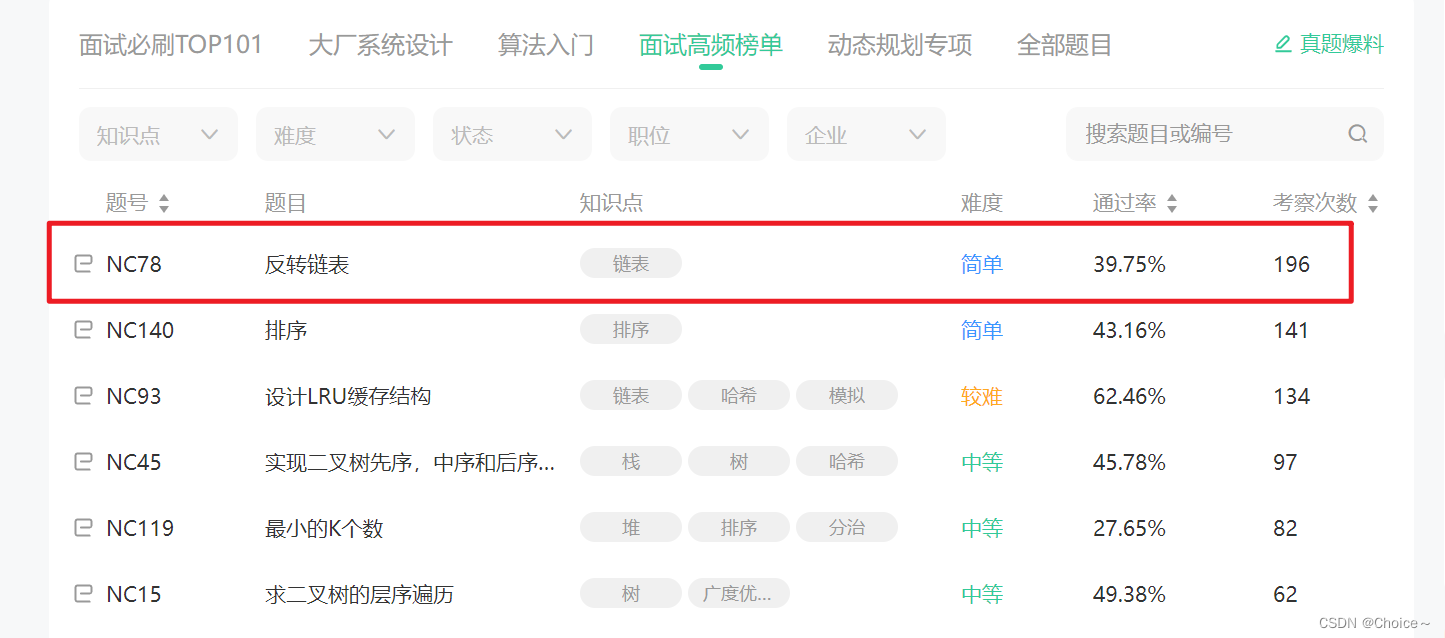
编辑2.NC78 反转链表

描述：

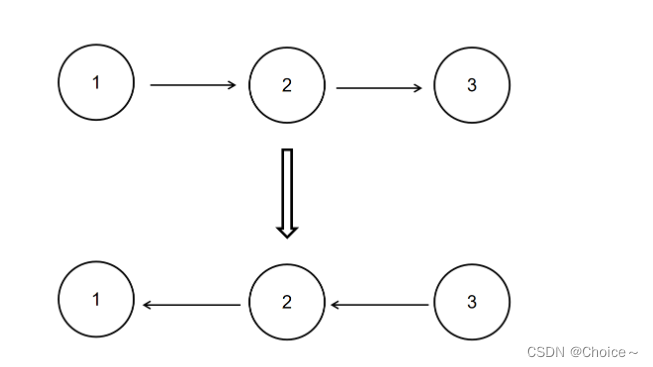
给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头。

数据范围： 0\leq n\leq10000≤n≤1000

要求：空间复杂度 O(1)O(1) ，时间复杂度 O(n)O(n) 。

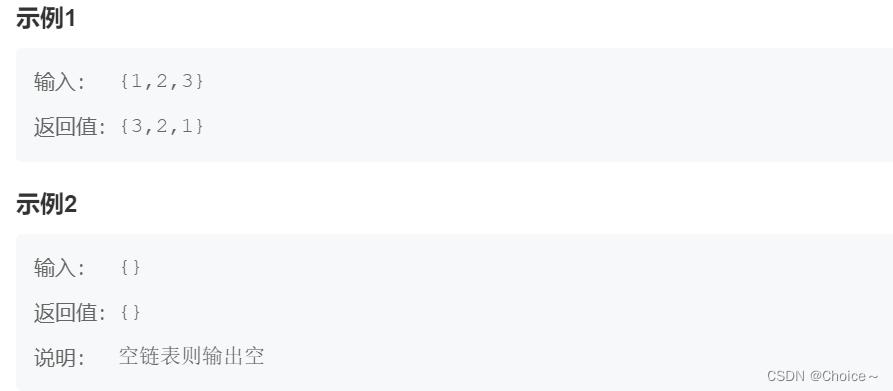
如当输入链表{1,2,3}时，

经反转后，原链表变为{3,2,1}，所以对应的输出为{3,2,1}。

以上转换过程如下图所示：

编辑

我们看输出样式

编辑

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 *
 * C语言声明定义全局变量请加上static，防止重复定义
 *
 * C语言声明定义全局变量请加上static，防止重复定义
 */

/**
 * 
 * @param pHead ListNode类 
 * @return ListNode类
 */
struct ListNode* ReverseList(struct ListNode* pHead ) {
    // write code here
}

相关企业职位有百度快手，大企 ...

编辑

解法一：迭代

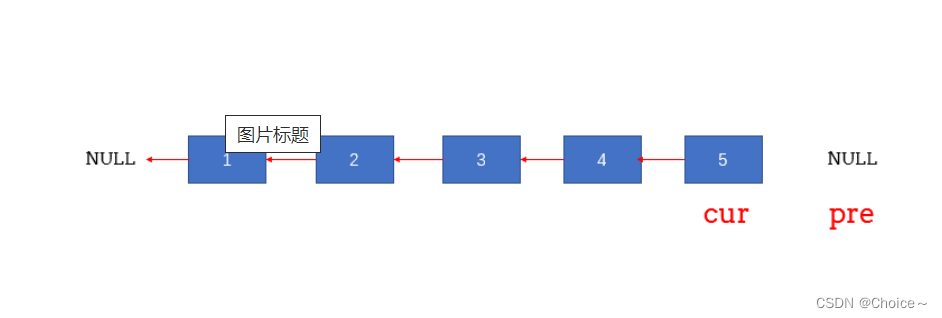
在遍历链表时，将当前节点的next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

图解：编辑

Java参考代码：

/*

public class ListNode {

int val;

ListNode next = null;

ListNode(int val) {

this.val = val;

}

}*/

public class Solution {

public ListNode ReverseList(ListNode head) {

//pre指针：用来指向反转后的节点，初始化为null

ListNode pre = null;

//当前节点指针

ListNode cur = head;

//循环迭代

while(cur!=null){

//Cur_next 节点，永远指向当前节点cur的下一个节点

ListNode Cur_next = cur.next;

//反转的关键：当前的节点指向其前一个节点(注意这不是双向链表，没有前驱指针)

cur.next = pre;

//更新pre

pre = cur;

//更新当前节点指针

cur = Cur_next ;

}

//为什么返回pre？因为pre是反转之后的头节点

return pre;

}

复杂度分析：

时间复杂度：O(N)，其中 N 是链表的长度。需要遍历链表一次。

空间复杂度：O(1)，常数空间复杂度

解法二：递归

使用递归函数，一直递归到链表的最后一个结点，该结点就是反转后的头结点，记作 ans
此后，每次函数在返回的过程中，让当前结点的下一个结点的 next 指针指向当前节点。
同时让当前结点的 next 指针指向NULL ，从而实现从链表尾部开始的局部反转
当递归函数全部出栈后，链表反转完成。

C++参考代码：

/*

struct ListNode {

int val;

struct ListNode *next;

ListNode(int x) :

val(x), next(NULL) {

}

};*/

class Solution {

public:

ListNode* ReverseList(ListNode* pHead) {

//特判：注意不要漏掉pHead->next==NULL的情况

if(pHead==NULL || pHead->next==NULL){

return pHead;

}

//递归调用

ListNode* ans = ReverseList(pHead->next);

//让当前结点的下一个结点的 next 指针指向当前节点

pHead->next->next=pHead;

//同时让当前结点的 next 指针指向NULL ，从而实现从链表尾部开始的局部反转

pHead->next=NULL;

return ans;

}

};

复杂度分析：

时间复杂度：O(N)，其中 N 是链表的长度。需要对链表的每个节点进行反转操作。

空间复杂度：O(N)，其中 N 是链表的长度。空间复杂度主要取决于递归调用的栈空间，最多为 N 层

算法思路三：使用额外栈

解题思路：

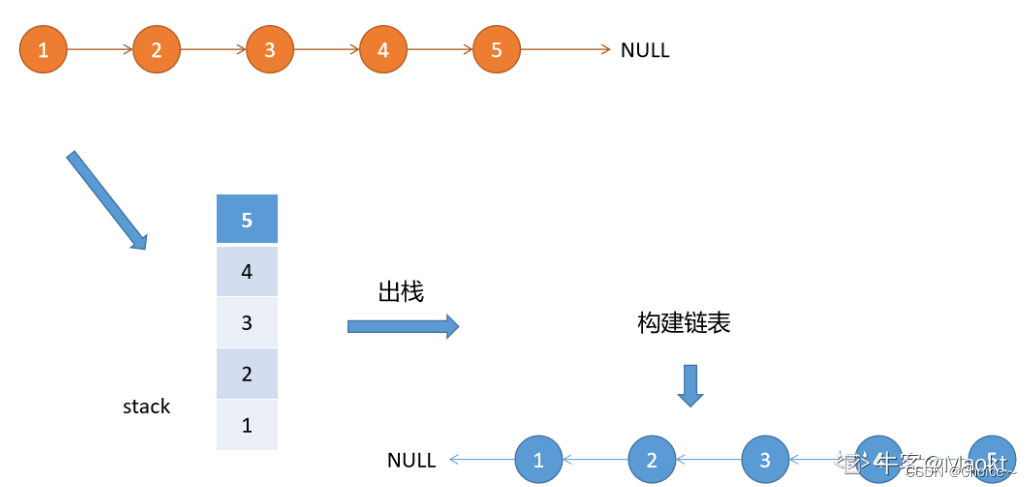
新建额外的新栈 stack

循环遍历原链表，并将链表元素入栈，遍历结束后，将栈内元素依次出栈并建立链表

图解：

编辑

代码展示：

public ListNode ReverseList(ListNode head) {

Stack<ListNode> stack = new Stack<>();

//把链表节点全部摘掉放到栈中

while (head != null) {

stack.push(head);

head = head.next;

}

if (stack.isEmpty())

return null;

ListNode node = stack.pop();

ListNode dummy = node;

//栈中的结点全部出栈，然后重新连成一个新的链表

while (!stack.isEmpty()) {

ListNode tempNode = stack.pop();

node.next = tempNode;

node = node.next;

}

//最后一个结点就是反转前的头结点，一定要让他的next

//等于空，否则会构成环

node.next = null;

return dummy;

}

复杂度分析：

时间复杂度O(N)：N表示链表长度

空间复杂度O(N)：辅助栈空间

今天就到这，欢迎成为牛客网的一员！！！点击有惊喜哦🙌编辑

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

加入云驻计划，成为创作者

华为云周边好礼
免费体验产品
特殊身份标识
线下官方门票
内部专家零距离
与10000+优质创作者共同成长

立即加入

算法面试高频题解指南【一】

1.NC110 旋转数组

描述：

探讨：

算法思想一：使用额外数组

代码展示：

复杂度分析

算法思想二：数组翻转

解题思路：

代码展示：

复杂度分析

算法思想三：数组变换

代码展示：

复杂度分析

​编辑2.NC78 反转链表

描述：

解法一：迭代

Java参考代码：

解法二：递归

C++参考代码：

算法思路三：使用额外栈

代码展示：

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

推荐阅读

相关产品

编辑2.NC78 反转链表