数学建模学习笔记（二十一）时间序列小白指南（下）

上两篇整理了ARIMA的建模和编程，此篇再加以拓展，考虑季节性

季节性时间序列SARIMA
在进行季节性时间序列稳定性检测之前，首先判断
a.时间序列是否有季节性
b.时间序列在什么频率上有季节性。结果会作为时间序列稳定性检测的参数输入
（季节性：比如，旅游有淡旺季）

使用季节差分方法，消除数据的周期性变化
季节差分算子：

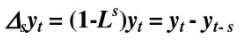
MATLAB实战 ——SARIMA预测游客人数
这里代码和上篇内容基本一致，具体步骤可以见上篇不再赘述，放上代码：

close all
clear all
%% 1.加载数据
data=xlsread('sarima_data.xls');
S = 12; %季节性序列变化周期
step = 12;
% 通常P和Q不大于3
%% 2.确定季节性与非季节性差分数，D取默认值1，d从0至3循环，平稳后停止
for d = 0:3
    D1 = LagOp({1 -1},'Lags',[0,d]);     %非季节差分项的滞后算子
    D12 = LagOp({1 -1},'Lags',[0,1*S]);  %季节差分项的滞后算子
    D = D1*D12;          %相乘
    dY = filter(D,data); %对原数据进行差分运算
    if(getStatAdfKpss(dY)) %数据平稳
        disp(['非季节性差分数为',num2str(d),'，季节性差分数为1']);
        break;
    end
end
%% 3.确定阶数ARlags,MALags,SARLags,SMALags
max_ar = 3;    %ARlags上限
max_ma = 3;    %MALags上限
max_sar = 3;   %SARLags上限
max_sma = 3;   %SMALags上限
try
    [AR_Order,MA_Order,SAR_Order,SMA_Order] = SARMA_Order_Select(dY,max_ar,max_ma,max_sar,max_sma,S,d); %自动定阶 
catch ME %捕捉错误信息
    msgtext = ME.message;
    if (strcmp(ME.identifier,'econ:arima:estimate:InvalidVarianceModel'))
         msgtext = [msgtext,'  ','无法进行arima模型估计，这可能是由于用于训练的数据长度较小，而要进行拟合的阶数较高导致的，请尝试减小max_ar,max_ma,max_sar,max_sma的值'];
    end
    msgbox(msgtext, '错误')
end
disp(['ARlags=',num2str(AR_Order),',MALags=',num2str(MA_Order),',SARLags=',num2str(SAR_Order),',SMALags=',num2str(SMA_Order)]);
%% 4.残差检验
Mdl = creatSARIMA(AR_Order,MA_Order,SAR_Order,SMA_Order,S,d);  %创建SARIMA模型 
try
    EstMdl = estimate(Mdl,data);
catch ME %捕捉错误信息
    msgtext = ME.message;
    if (strcmp(ME.identifier,'econ:arima:estimate:InvalidVarianceModel'))
         msgtext = [msgtext,'  ','无法进行arima模型估计，这可能是由于用于训练的数据长度较小，而要进行拟合的阶数较高导致的，请尝试减小max_ar和max_ma的值']
    end
    msgbox(msgtext, '错误')
    return
end
[res,~,logL] = infer(EstMdl,data);   %res即残差

stdr = res/sqrt(EstMdl.Variance);
figure('Name','残差检验','Visible','on')
subplot(2,3,1)
plot(stdr)
title('Standardized Residuals')
subplot(2,3,2)
histogram(stdr,10)
title('Standardized Residuals')
subplot(2,3,3)
autocorr(stdr)
subplot(2,3,4)
parcorr(stdr)
subplot(2,3,5)
qqplot(stdr)
% Durbin-Watson 统计是计量经济学分析中最常用的自相关度量
diffRes0 = diff(res);  
SSE0 = res'*res;
DW0 = (diffRes0'*diffRes0)/SSE0 % Durbin-Watson statistic，该值接近2，则可以认为序列不存在一阶相关性。
%% 5.预测
[forData,YMSE] = forecast(EstMdl,step,data);   %matlab2018及以下版本写为Predict_Y = forecast(EstMdl,step,'Y0',Y);   matlab2019写为Predict_Y = forecast(EstMdl,step,Y);

lower = forData - 1.96*sqrt(YMSE); %95置信区间下限
upper = forData + 1.96*sqrt(YMSE); %95置信区间上限

figure('Visible','on')
plot(data,'Color',[.7,.7,.7]);
hold on
h1 = plot(length(data):length(data)+step,[data(end);lower],'r:','LineWidth',2);
plot(length(data):length(data)+step,[data(end);upper],'r:','LineWidth',2)
h2 = plot(length(data):length(data)+step,[data(end);forData],'k','LineWidth',2);
legend([h1 h2],'95% 置信区间','预测值',...
	     'Location','NorthWest')
title('Forecast')
hold off

function stat = getStatAdfKpss(data)
try 
    stat = adftest(data) && ~kpsstest(data);
catch ME
    msgtext = ME.message;
    if (strcmp(ME.identifier,'econ:adftest:EffectiveSampleSizeLessThanTabulatedValues'))
         msgtext = [msgtext,'  ','单位根检验无法进行，数据长度不足'];
    end
    msgbox(msgtext, '错误')
end
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
 

这段代码差不多花了3-5分钟再跑出结果~如果运行卡住，稍等即可

其它时间序列方法补充：
一次移动平均法 (SMA)
通过对过去的几个期间求平均值并将过去的平均值投射到将来，使历史数据平滑化
此方法最适合没有趋势或季节性的波动数据。此方法将生成平直线预测。

二次移动平均法
对一次移动平均数再进行第二次移动平均

close all
clear,clc% 统计数据 实际值
arr = [1532 1645 1770 1790 1551 1840 1880 1830 1921]’;
[m,nn]=size(arr)
N = 2 % 步长
% 1次平滑
s1 = zeros(m,1);
for i=N:ms1(i) = sum(arr(i-N+1:i,:))/N;
endsx1 = s1% 2次 平滑
s2 = zeros(m,1);
for i=2*N-1:ms2(i) = sum(s1(i-N+1:i,:))/N;
end
sx2 = s2 
% 计算bai线性趋势的截距和斜率
% a = 2*m1 - m2
% b = 2/(N-1)*(m1 - m2)
a = 2*s1 - s2;
b = 2/(N-1)*(s1 - s2);
a(1:2*N-2) = 0;b(1:2*N-2) = 0;
ab% 预测% 
fx(t) = a(t) + b(t)*tou % 
fx(t+tou) = a(t) + b(t)*tou
% tou表示预测超前期数；
fx(t)表示第t+tou期的预测值 
% fx(t+tou)表示第t+tou期的预测值
tou1 = 1 % 超前预测1期
fx1 = a + b *tou1tou2 = 2 % 超前预测2期fx2 = a + b *tou2

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
 

注意事项：
（1）季节变动法预测需要筹集至少三年以上的资料
（2）移动平均法在短期预测中较准确，长期预测中效果较差；
（3）移动平均可以消除或减少时间序列数据受偶然性因素干扰而产生的随机变动影响。
（4）一次移动平均法适用于具有明显线性趋势的时间序列数据的预测；一次移动平均法只能用来对下一期进行预测，不能用于长期预测。
必须选择合理的移动跨期：跨期越大对预测的平滑影响也越大，移动平均数滞后于实际数据的偏差也越大。跨期太小则又不能有效消除偶然因素的影响。跨期取值可在3~20 间选取。
（5）二次移动平均法与一次移动平均法相比，其优点是大大减少了滞后偏差，使预测准确性提高；二次移动平均只适用于短期预测。

文章来源: zstar.blog.csdn.net，作者：zstar-_，版权归原作者所有，如需转载，请联系作者。

原文链接：zstar.blog.csdn.net/article/details/113545637