数学建模学习笔记（十八）SIER模型灵敏度分析(matlab求解)

什么是灵敏度分析？
简单得来说，就是当模型中有一些参数不确定时，需要多取一些值比较结果，来验证其灵敏性。下面就以上篇写到的传染病模型进行分析：

例如：
在使用传染病模型时，自行选取了传染概率B为0.03，我们需要对其进行灵敏度分析

自定义matlab函数

function funname(x1)
N = 38000;                                                                  %人口总数
E = 0;                                                                      %潜伏者
I = 1;                                                                      %传染者
S = N - I;                                                                  %易感者
R = 0;                                                                      %康复者
r = 20;                                                                     %感染者接触易感者的人数
B = x1;                                                                     %传染概率
a = 0.1;                                                                    %潜伏者转化为感染者概率
y = 0.1;                                                                    %康复概率

T = 1:182;
for idx = 1:length(T)-1
    S(idx+1) = S(idx) - r*B*S(idx)*I(idx)/N;
    E(idx+1) = E(idx) + r*B*S(idx)*I(idx)/N-a*E(idx);
    I(idx+1) = I(idx) + a*E(idx) - y*I(idx);
    R(idx+1) = R(idx) + y*I(idx);
end

for j=1:26
    zi(j)=I(j*7)-I(j*7-6);
    kf(j)=R(j*7)-R(j*7-6);
    y(j)=zi(j)+kf(j);                                                      %每日新增=一周内感染患者+一周内康复患者
end

x=1:26;
plot(x,y);
hold on;
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
 

再调用不同的参数：

funname(0.03)
funname(0.031)
funname(0.0305)
funname(0.0315)
funname(0.032)
funname(0.0325)
funname(0.0295)
funname(0.029)
funname(0.0285)
xlabel('week');ylabel('New cases')

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
 

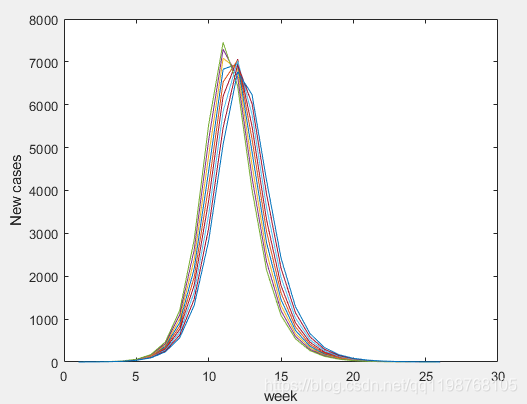
结果如图：

文章来源: zstar.blog.csdn.net，作者：zstar-_，版权归原作者所有，如需转载，请联系作者。

原文链接：zstar.blog.csdn.net/article/details/113473838