【计算机视觉】数字图像处理基础知识题
本文是计算机视觉课程的平时练习汇总,所用到的图片和实验报告的获取方式见文末
题1
1、产生下图所示亮块图像 f1(x,y)(128×128大小,暗处=0,亮处=255),对其进行FFT。

(1)同屏显示原图f1和FFT(f1)的幅度谱图;
(2)若令f2(x,y)=(-1)x+y f1(x,y),重复以上过程,比较二者幅度谱的异同,简述理由;
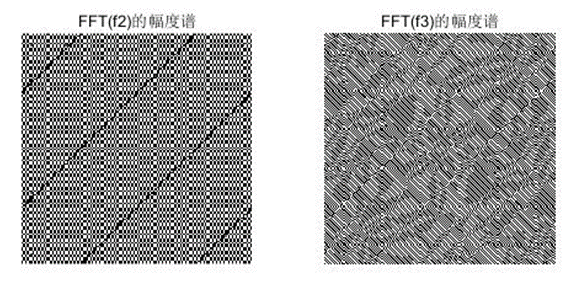
(3)若将f2(x,y)顺时针旋转45度得到f3(x,y),试显示FFT(f3)的幅度谱,并与FFT(f2)的幅度谱进行比较。
(1) 原图f1和FFT(f1)的幅度谱图如图1所示

(2) 令 f 2 ( x , y ) = ( − 1 ) ( x + y ) f 1 ( x , y ) f2(x,y)=(-1)^(x+y) f1(x,y) f2(x,y)=(−1)(x+y)f1(x,y),f2和FFT(f2)的幅度谱图如图2所示。

两者的异同:
不同点:f2的频谱是对f1频谱的移位。
相同点:频谱的实质没有改变,幅度等都没有发生变化。
(3) 将f2(x,y)顺时针旋转45度得到f3(x,y),FFT(f2)的幅度谱和FFT(f3)的幅度谱如图3所示。
matlab代码:
% 生成第一问图像
f1=zeros(128,128);
for i=38:1:90
for j=58:1:70
f1(i,j)=255;
end
end
% 第一小问
figure(1)
subplot(1,2,1);
imshow (f1);
subplot(1,2,2);
imshow (fft2(f1));
% 第二小问
for i=1:1:128
for j=1:1:128
f2(i,j)=(-1)^(i+j)*f1(i,j);
end
end
figure(2);
subplot(1,2,1);
imshow (f2);
subplot(1,2,2);
imshow (fft2(f2));
% 第三小问
figure(3);
f3=imrotate(f2,-45,'bilinear');%将f2顺时针旋转45度
subplot(1,2,1);
imshow(fft2(f2));%显示f2的频谱
title('FFT(f2)的幅度谱');
subplot(1,2,2);
imshow(fft2(f3));%显示f3的频谱
title('FFT(f3)的幅度谱');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
题2
2.对512x512大小、256级灰度的数字图像l
ena进行频域的理想低通、高通滤波,同屏显示原图、幅度谱图和低通、高通滤波的结果图。
本题采用了高斯滤波器来对图像进行低通和高通滤波。滤波器公式如下:
低通滤波(D_0为截止频率,本实验中取值为30Hz):

高通滤波(D_0为截止频率,本实验中取值为30Hz):
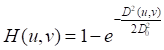

如图所示,图像经过低通滤波后,图像主体仍然保留,但羽毛、轮廓等高频信息被滤除,图像经过高通滤波后,图像主体信息被滤除,图像轮廓信息被提取出来。
matlab代码:
data=imread('D:\Desktop\计算机视觉\平时作业\img\lena.bmp');
figure(1);
subplot(2,2,1)
imshow(data);
title('原图');
subplot(2,2,2);
imshow(fft2(data));
title('幅度谱图');
%低通滤波
s=fftshift(fft2(data));
[M,N]=size(s);
n=2;
%GLPF滤波d0=30
d0=30;
n1=floor(M/2); %对M/2进行取整
n2=floor(N/2); %对N/2进行取整
for i=1:M
for j=1:N
d=sqrt((i-n1)^2+(j-n2)^2); %点(i,j)到傅立叶变换中心的距离
h=1*exp(-1/2*(d^2/d0^2)); %GLPF滤波函数
s(i,j)=h*s(i,j); %GLPF滤波后的频域表示
end
end
s=ifftshift(s); %对s进行反FFT移动
s=uint8(real(ifft2(s)));
subplot(2,2,3);
imshow(s);
title('低通滤波');
%高通滤波
p=fftshift(fft2(data));
[M,N]=size(p); %分别返回p的行数到M中,列数到N中
n=2; %对n赋初值
%GHPF滤波d1=30
d1=30;
n3=floor(M/2);
n4=floor(N/2);
for i=1:M
for j=1:N
dd=sqrt((i-n3)^2+(j-n4)^2); %点(i,j)到傅立叶变换中心的距离
h1=1-exp(-1/2*(dd^2/d1^2)); %GHPF滤波函数
p(i,j)=h1*p(i,j); %GHPF滤波后的频域表示
end
end
p=ifftshift(p); %对p进行反FFT移动
p=uint8(real(ifft2(p)));
subplot(2,2,4);
imshow(p);
title('高通滤波');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
题3
3、对图像pollen进行如下处理:
(1)使用直方图均衡化及直方图规定化,展示对比度拉伸的效果,要求先转化为灰度级L=8,再按要求转化,写出详细的过程,其中规定直方图为0,0,0,0.15,0.20,0.30,0.20,0.15
首先将图像pollen转化为灰度级L=8,如图5所示:

之后将其进行直方图均衡化和规定化,如图6所示:
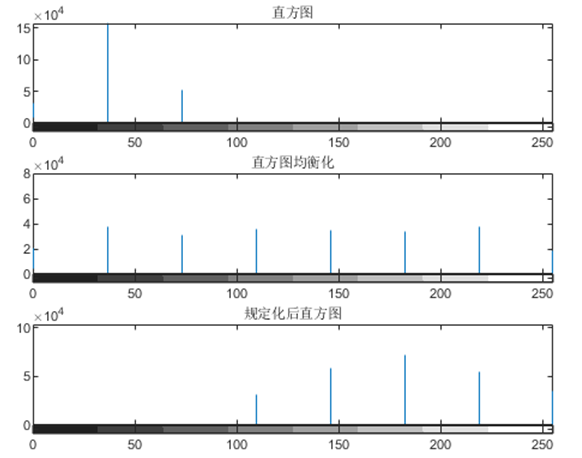
从图中可以看出,原图中像素点大多为2/8和3/8灰度级,直方图均衡化之后,原图中像素点在各灰度级上均匀分布。直方图规定化之后,像素点的分布情况满足题目预设的分布条件。
(2)对直方图均衡化后的图像加入高斯噪声,用4-邻域平均法和中值滤波平滑加噪声图像(图像四周边界不处理,下同),同屏显示原图像、加噪图像和处理后的图像。
① 不加门限;
② 加门限 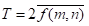 ,(其中
,(其中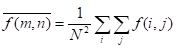 )
)
原图像、加噪图像、不加门限平滑后图像,加门限后平滑后图像如图7所示:

matlab代码:
% 第一小问
I=imread('D:\Desktop\计算机视觉\平时作业\img\pollen.tif');
figure(1);
subplot(1,2,1);
imshow(I);
title('原图');
% L=8灰度级
[wid, hei] = size(I);
img8 = zeros(wid, hei);
for i=1:wid
for j=1:hei
img8(i,j)=floor(I(i,j)/32);
end
end
subplot(1,2,2);
imshow(uint8(img8),[0,7]);
title('灰度级L=8');
figure(2);
subplot(3,2,[1,2]);
imhist(I,8);
title('直方图');
J=histeq(I);
subplot(3,2,[3,4]);
imhist(J,8);
title('直方图均衡化');
subplot(3,2,[5,6]);
hgram=[0,0,0,0.15,0.20,0.30,0.20,0.15];
H=histeq(I,hgram);
imhist(H,8);
title('规定化后直方图');
% 第二小问
figure(3);
I1=imnoise(I,'gaussian'); %加高斯噪声
H1=[0 1 0;1 0 1;0 1 0]/4; %4×4领域模板
J1=imfilter(J,H1); %领域平均
subplot(1,4,1);
imshow(I); %显示图像I
title('原图像');
subplot(1,4,2);
imshow(I1);
title('加噪声后图像');
subplot(1,4,3);
imshow(J1);
title('不加门限平滑后图像');
%加门限后滤波
T= 2*sum(I1(:))/500^2;
% T= 0;
im_T = zeros(500,500);
for i = 1:500
for j = 1:500
if abs(I1(i,j) - J(i,j))>T
im_T(i,j) = J(i,j);
else
im_T(i,j) = I1(i,j);
end
end
end
subplot(1,4,4);
imshow(im_T);
title('加门限后');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
题4
4、(1)用Laplacian锐化算子(分 α = 1 \alpha=1 α=1和 α = 2 \alpha=2 α=2两种情况)对512x5
12大小、256级灰度的数字图像lena进行锐化处理,显示处理前、后图像。处理前后的图像如图8所示:
(2) 若令

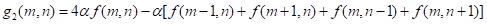
则回答如下问题:
① f ( m , n ) f(m,n) f(m,n) 、 g 1 ( m , n ) g_1(m,n) g1(m,n) 和 g 2 ( m , n ) g_2(m,n) g2(m,n)之间有何关系?
三者的关系为: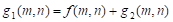
② g 2 ( m , n ) g_2(m,n) g2(m,n)代表图像中的哪些信息?
g 2 ( m , n ) g_2(m,n) g2(m,n)代表了原图像中的二阶梯度信息。
③ 由此得出图像锐化的实质是什么?
图像锐化的实质是将原图像与梯度信息叠加,对目标边缘进行增强。
matlab代码
I=imread('D:\Desktop\计算机视觉\平时作业\img\lena.jpg');
figure(1);
subplot(1,3,1);imshow(I);title('原始图像');
L=fspecial('laplacian');
L1=[0 -1 0;-1 5 -1;0 -1 0];
L2=[0 -2 0;-2 9 -2;0 -2 0];
LP1=imfilter(I,L1,'replicate');% α=1时的拉普拉斯算子
LP2=imfilter(I,L2,'replicate');% α=2时的拉普拉斯算子
subplot(1,3,2);imshow(LP1);title('Laplacian算子α=1锐化图像');
subplot(1,3,3);imshow(LP2);title('Laplacian算子α=2锐化图像');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
题5
5、分别利用Roberts、Prewitt、Sobel、Laplacian、Canny边缘检测算子,对256级灰度的自然图像iris-Na、光学遥感图像bridge-RS、SAR图像road-SAR进行边缘检测,显示处理前、后图像,并阐述不同算法和数据源对结果的影响。
自然图像iris-Na:

光学遥感图像bridge-RS:

SAR图像road-SAR:

不同算法结果分析:
Roberts算子采用对角方向相邻两像素之差,也被称作4点差分法,对噪声较敏感。从三种图像上可以看出,使用Roberts算子进行边缘检测,检测出的结果较为稀疏,仅包含部分图像主题信息。
Prewitt算子先求平均,再求差分来计算梯度,也被称作平均差分法。从三种图像上可以看出,使用Prewitt算子进行边缘检测,检测出的结果比Roberts算子的结果更加稠密一些,同时能够一定程度上抑制噪声的干扰。
Sobel算子当前行或列对应的值加权后,再进行平均和差分,也被称作加权平均差分法。从三种图像上可以看出,使用Sobel算子结果和使用Prewitt算子的结果近似,但其边缘模糊的程度要略低于Prewitt算子。
Laplacian算子是求像素点的二阶偏导,优点是各向同性、线性和唯一不变性;对孤立点及线段的检测效果好,缺点是对噪声敏感,对噪声有双倍加强作用;不能检测出边的方向,常产生双像素的边缘。相比与上述三种算子,Laplacian算子得到的结果得到的细节信息更多,但同时对于噪声较多的road-SAR效果较差。
Canny算子基本思想是找寻一幅图像中灰度强度变化最强的位置,首先它用高斯滤波来平滑图像,然后找寻图像的强度梯度,之后应用非最大抑制技术来消除边误检,最后应用双阈值的方法来检测和连接边界。从结果图上可以发现,Canny算子检测的结果最为丰富,很多细节信息都被检测出来,同时由于它独特的处理方法,边缘部分比较清晰。
不同数据源分析:
本题中使用的三种数据源,格式并不相同。检测时首先将图像转换成灰度图,然后再进行检测。其中,iris-Na和bridge-RS图像的噪声较少,road-SAR图像的噪声较多。
对于iris-Na图像,图像主体是鸢尾花,背景包含比较杂乱的枝叶信息。对于该图像,Roberts算子,Prewitt算子和Sobel算子都能较好地将图像主体边缘检测出来。Laplacian算子和Canny算子在此基础上能够检测出更多的细节信息。
对于bridge-RS图像,Roberts算子,Prewitt算子和Sobel算子同样能够将图像的主体桥梁检测出来,但对于两岸细节信息较为忽略,Laplacian算子和Canny算子能够捕捉到主体和细节信息。
对于road-SAR图像,由于包含了较多的噪声信息,Roberts算子,Prewitt算子的检测效果不太理想,而Sobel算子能够较少地受到噪声的影响,检测出图中两条公路的主体信息。Laplacian算子和Canny算子都在一定程度上将噪声信息进行了放大增强,导致最终结果的可识别性不如Sobel算子。
matlab代码:
clear;
close all;
Img=imread('D:\Desktop\计算机视觉\平时作业\img\iris-Na.tif');
% Img=imread('D:\Desktop\计算机视觉\平时作业\img\bridge-RS.jpg');
% Img=imread('D:\Desktop\计算机视觉\平时作业\img\road-SAR.png');
I = rgb2gray(Img);
figure(1)
%Roberts梯度法锐化
subplot(2,3,1);imshow(Img);title('原始图像');
S=edge(I,'Roberts');
subplot(2,3,2);imshow(S);title('Roberts梯度法锐化图像');
%Prewitt算子锐化
S=edge(I,'Prewitt');
subplot(2,3,3);imshow(S);title('Prewitt算子锐化图像');
%Sobel算子锐化
S=edge(I,'Sobel');
subplot(2,3,4);imshow(S);title('Sobel算子锐化图像');
%Laplacian算子锐化
S=edge(I,'log');
subplot(2,3,5);imshow(S);title('Laplacian算子锐化图像');
%Canny算子锐化
Cimg = edge(I,'canny');
subplot(2,3,6);imshow(Cimg);title('Canny算子锐化图像');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
图片和实验报告
图片和实验报告下载链接:https://download.csdn.net/download/qq1198768105/85837789
文章来源: zstar.blog.csdn.net,作者:zstar-_,版权归原作者所有,如需转载,请联系作者。
原文链接:zstar.blog.csdn.net/article/details/125537048
- 点赞
- 收藏
- 关注作者


评论(0)