数学建模暑期集训22：图论最短路径问题——Dijkstra算法和Floyd算法
【摘要】
迪杰斯特拉Dijkstra算法
Dijkstra是图论中经典的算法，可以计算图中一点到其它任意一点的最短路径。 学过数据结构的应该都接触过，因此具体的演示这里不再赘述。 完整的演示可以参看 图论最短距离...
迪杰斯特拉Dijkstra算法
Dijkstra是图论中经典的算法，可以计算图中一点到其它任意一点的最短路径。
学过数据结构的应该都接触过，因此具体的演示这里不再赘述。
完整的演示可以参看
图论最短距离(Shortest Path)算法动画演示-Dijkstra(迪杰斯特拉)和Floyd(弗洛伊德)
算法的缺点：不能处理带负权重的图。
matlab实现
1.绘制图形
下面以这副图为例将它绘制：
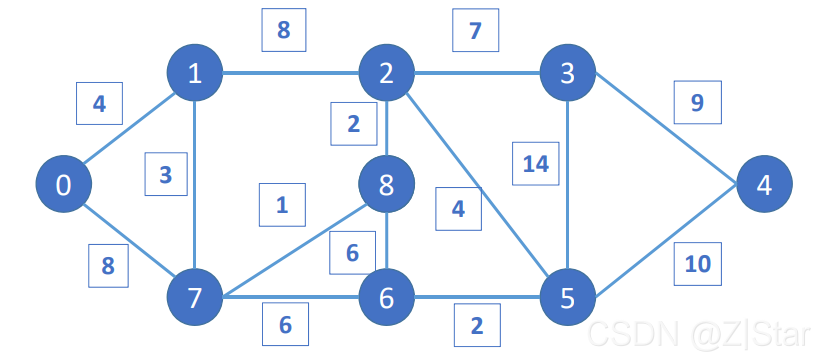
注：matlab的图节点要从1开始编号。
绘图代码：
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
- 1
- 2
- 3
- 4
- 5
s代表起始点，t代表终点，w代表起始点到终点边上的权重。
例如，第一组 [s,t,w]=[9,1,4]代表9号节点向1号节点连接一条边，边权重为4。
graph函数代表绘制无向图
若要绘制有向图，改为digraph即可。
绘制效果：
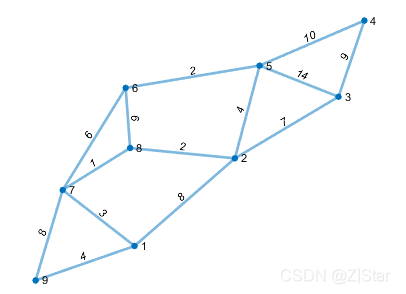
2.求解两点之间的最短路径
matlab内置了求解两点最短路径的函数shortestpath
set( gca, 'XTick', [], 'YTick', [] );
[P,d] = shortestpath(G, 9, 4) %注意：该函数matlab2015b之后才有哦
- 1
- 2
P用来存贮路径的经过节点，d代表距离。
(9,4)代表求解9号节点到4号节点的最短距离。
3.求解任意两点的最短路径矩阵
上面的函数只能求解指定两点之间的距离，若要批量求解多个节点，可以用 distances函数。
D = distances(G)
- 1
D用来存贮任意两点之间最短距离矩阵。
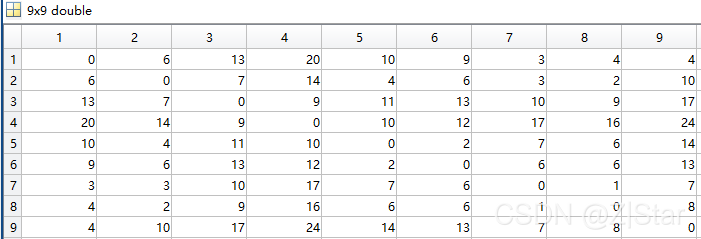
D(9,4)
- 1
D矩阵的第9行第4列代表9到4的最短路径，得到24，和上面的结果一致。
4.找出给定范围内的所有点
matlab还内置了一个函数nearest，可以在给定范围内找出所有符合的节点。
[nodeIDs,dist] = nearest(G, 2, 10)
- 1
nearest(G, 2, 10)代表求解在图G中的2号节点中10范围之内的其它点。
nodeIDs存贮节点ID，dist存储距离。
完整代码（包含图中高亮）
% 注意哦，Matlab中的图节点要从1开始编号，所以这里把0全部改为了9
% 编号最好是从1开始连续编号，不要自己随便定义编号
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
set( gca, 'XTick', [], 'YTick', [] );
[P,d] = shortestpath(G, 9, 4) %注意：该函数matlab2015b之后才有哦
% 在图中高亮我们的最短路径
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2); %首先将图赋给一个变量
highlight(myplot, P, 'EdgeColor', 'r') %对这个变量即我们刚刚绘制的图形进行高亮处理（给边加上r红色）
% 求出任意两点的最短路径矩阵
D = distances(G) %注意：该函数matlab2015b之后才有哦
D(1,2) % 1 -> 2的最短路径
D(9,4) % 9 -> 4的最短路径
% 找出给定范围内的所有点 nearest(G,s,d)
% 返回图形 G 中与节点 s 的距离在 d 之内的所有节点
[nodeIDs,dist] = nearest(G, 2, 10) %注意：该函数matlab2016a之后才有哦
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
弗洛伊德Floyd算法
Floyd算法能够一次性的求出任意两点之间的最短路径，且图中允许出现负权重。
缺点：时间复杂度高。
算法核心：三层循环
核心思想:
伪代码描述：
for k from 1 to |V| //中间节点K
for i from 1 to |V| //初始节点i
for j from 1 to |V| //终点节点j
if dist[i][j] > dist[i][k] + dist[k][j]
dist[i][j] ← dist[i][k] + dist[k][j]
- 1
- 2
- 3
- 4
- 5
matlab实现
1.Floyd_algorithm函数
用于求解一个权重邻接矩阵任意两个节点之间的最短路径
function [dist,path] = Floyd_algorithm(D)
%% 该函数用于求解一个权重邻接矩阵任意两个节点之间的最短路径
% 输入：
% D是权重邻接矩阵
% 输出：
% dist是最短距离矩阵，其元素dist_ij表示表示i,j两个节点的最短距离
% path是路径矩阵，其元素path_ij表示起点为i，终点为j的两个节点之间的最短路径要经过的节点
n = size(D,1); % 计算节点的个数
% 初始化dist矩阵
dist = D;
% 下面我们来初始化path矩阵
path = zeros(n);
for j = 1:n
path(:,j) = j; % 将第j列的元素变为j
end
for i = 1:n
path(i,i) = -1; % 将主对角线元素变为-1
end
% 下面开始三个循环
for k=1:n % 中间节点k从1- n 循环
for i=1:n % 起始节点i从1- n 循环
for j=1:n % 终点节点j从1-n 循环
if dist(i,j)>dist(i,k)+dist(k,j) % 如果i,j两个节点间的最短距离大于i和k的最短距离+k和j的最短距离
dist(i,j)=dist(i,k)+dist(k,j); % 那么我们就令这两个较短的距离之和取代i,j两点之间的最短距离
path(i,j)=path(i,k); % 起点为i，终点为j的两个节点之间的最短路径要经过的节点更新为path(i,k)
end
end
end
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
2.print_all_path函数
求解一个权重邻接矩阵任意两个节点之间的最短路径,并打印所有的结果出来
function [] = print_all_path(D)
%% 该函数的作用是求解一个权重邻接矩阵任意两个节点之间的最短路径,并打印所有的结果出来
% 输入：
% D是权重邻接矩阵
% 输出：无
[dist,path] = Floyd_algorithm(D); % 调用之前的Floyd_algorithm函数
n = size(D,1);
if n == 1
warning('请输入至少两阶以上的权重邻接矩阵') % 在屏幕中提示警告信息
return; % 不运行下面的语句，直接退出函数
end
for i = 1:n
for j = 1:n
if i ~= j % 不等号用~=表示
print_path(path,dist,i,j); % 调用之前的print_path函数
disp('-------------------------------------------')
disp(' ')
end
end
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
3.print_path函数
打印从i到j经过的最短路径
function [] = print_path(path,dist,i,j)
%% 该函数的作用是打印从i到j经过的最短路径
% 输入：
% path是使用floyd算法求出来的路径矩阵
% dist是使用floyd算法求出来的最短距离矩阵
% i是起始节点的编号
% j是终点节点的编号
% 输出：无
if i == j
warning('起点和终点相同，请检查后重新输入') % 在屏幕中提示警告信息
return; % 不运行下面的语句，直接退出函数
end
if path(i,j) == j % 如果path(i,j) = j，则有两种可能：
% （1）如果dist(i,j) 为 Inf , 则说明从i到j没有路径可以到达
if dist(i,j) == Inf
disp(['从',num2str(i),'到',num2str(j),'没有路径可以到达'])
% （2）如果dist(i,j) 不为 Inf , 则说明从i到j可直接到达，且为最短路径
else
disp(['从',num2str(i),'到',num2str(j),'的最短路径为'])
disp([num2str(i),' ---> ',num2str(j)])
disp(['最短距离为',num2str(dist(i,j))])
end
else % 如果path(i,j) ~= j，则说明中间经过了其他节点：
k = path(i,j);
result = [num2str(i),' ---> ']; % 初始化要打印的这个字符串
while k ~= j % 只要k不等于j, 就一直循环下去
result = [result , num2str(k) , ' ---> ' ]; % i先走到k这个节点处
k = path(k,j);
end
result = [result , num2str(k)];
disp(['从',num2str(i),'到',num2str(j),'的最短路径为'])
disp(result)
disp(['最短距离为',num2str(dist(i,j))])
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
4.使用案例
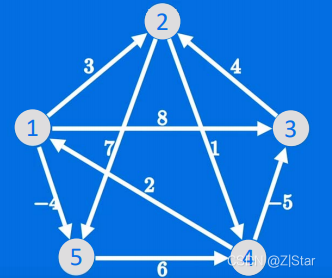
%% 首先将图转换为权重邻接矩阵D
n = 5; %一共五个节点
D = ones(n) ./ zeros(n); % 全部元素初始化为Inf
for i = 1:n
D(i,i) = 0; % 主对角线元素为0
end
D(1,2) = 3;
D(1,3) = 8;
D(1,5) = -4;
D(2,5) = 7;
D(2,4) = 1;
D(3,2) = 4;
D(4,3) = -5;
D(5,4) = 6;
D(4,1) = 2;
%% 调用Floyd_algorithm函数求解
[dist,path] = Floyd_algorithm(D)
print_path(path,dist,1,5)
print_path(path,dist,1,4)
print_path(path,dist,3,1)
clc
disp('下面我们打印任意两点之间的最短距离：')
print_all_path(D)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
运行之后，会产生两个矩阵dist和path。
dist用来记录两节点之间的最短距离。
path用来记录两节点之间的最短路径。
例如，从3到1的最短路径为：3–>2–>4–>1
附加资料
最后，附上一个神奇的网站，可以画出较为好看的图论图像。
Graph Editor
文章来源: zstar.blog.csdn.net，作者：zstar-_，版权归原作者所有，如需转载，请联系作者。
原文链接：zstar.blog.csdn.net/article/details/119924363
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）