【Android UI】贝塞尔曲线 ⑦ ( 使用 德卡斯特里奥算法 公式计算的 方法绘制三阶贝塞尔曲线示例 )

举报
韩曙亮 发表于 2022/08/04 23:51:02 2022/08/04
【摘要】 文章目录 一、使用 德卡斯特里奥算法 公式计算的 方法绘制三阶贝塞尔曲线二、代码示例 贝塞尔曲线参考 : https://github.com/venshine/BezierMaker ...

文章目录


贝塞尔曲线参考 : https://github.com/venshine/BezierMaker





一、使用 德卡斯特里奥算法 公式计算的 方法绘制三阶贝塞尔曲线


在之前的博客 【Android UI】贝塞尔曲线 ④ ( 使用 android.graphics.Path 提供的 cubicTo 方法绘制三阶贝塞尔曲线示例 ) 中 , 使用了 Android 官方提供的 API 绘制了贝塞尔曲线 ;

在本篇博客中 , 使用纯算法的方式 , 实现 三阶贝塞尔曲线 ;

使用的算法就是 根据 德卡斯特里奥算法 推导出的 递推公式 写出的算法 ;

递推公式如下 :

P i k = { P i , k = 0 ( 1 − t ) P i k − 1 + t P i + 1 k − 1 , k = 1 , 2 , ⋯   , n ; i = 0 , 1 , ⋯   , n − k P_i^k =

{Pi,k=0(1−t)Pk−1i+tPk−1i+1,k=1,2,⋯,n;i=0,1,⋯,n−k { P i , k = 0 ( 1 − t ) P i k − 1 + t P i + 1 k − 1 , k = 1 , 2 , ⋯ , n ; i = 0 , 1 , ⋯ , n − k
Pik​={Pi​,k=0(1−t)Pik−1​+tPi+1k−1​,k=1,2,⋯,n;i=0,1,⋯,n−k​

根据上述 贝塞尔曲线递推公式 , 可以得到一个递归算法 , 算法核心公式如下 :

p ( i , j ) = ( 1 − u ) × p ( i − 1 , j ) + u × p ( i − 1 , j − 1 ) p(i, j) = (1-u) \times p (i - 1, j) + u \times p (i - 1 , j - 1) p(i,j)=(1−u)×p(i−1,j)+u×p(i−1,j−1)

参考 【Android UI】贝塞尔曲线 ⑤ ( 德卡斯特里奥算法 | 贝塞尔曲线递推公式 )


完整的贝塞尔曲线上的点坐标算法如下 :

  • BezierX 方法用于计算 贝塞尔曲线上的 X 轴坐标点 ;
  • BezierY 方法用于计算 贝塞尔曲线上的 Y 轴坐标点 ;
    // 贝塞尔曲线控制点集合
    private ArrayList<PointF> mControlPoints = new ArrayList<>();

    /**
     * 贝塞尔曲线递归算法, 本方法计算 X 轴坐标值
     * @param i 贝塞尔曲线阶数
     * @param j 贝塞尔曲线控制点
     * @param u 比例 / 时间 , 取值范围 0.0 ~ 1.0
     * @return
     */
    private float BezierX(int i, int j, float u) {
        if (i == 1) {
            // 递归退出条件 : 贝塞尔曲线阶数 降为一阶
            // 一阶贝塞尔曲线点坐标 计算如下 :
            return (1 - u) * mControlPoints.get(j).x + u * mControlPoints.get(j + 1).x;
        }
        return (1 - u) * BezierX(i - 1, j, u) + u * BezierX(i - 1, j + 1, u);
    }

    /**
     * 贝塞尔曲线递归算法, 本方法计算 Y 轴坐标值
     * @param i 贝塞尔曲线阶数
     * @param j 贝塞尔曲线控制点
     * @param u 比例 / 时间 , 取值范围 0.0 ~ 1.0
     * @return
     */
    private float BezierY(int i, int j, float u) {
        if (i == 1) {
            // 递归退出条件 : 贝塞尔曲线阶数 降为一阶
            return (1 - u) * mControlPoints.get(j).y + u * mControlPoints.get(j + 1).y;
        }
        return (1 - u) * BezierY(i - 1, j, u) + u * BezierY(i - 1, j + 1, u);
    }

  
 

  
 

 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    •

参考博客 【Android UI】贝塞尔曲线 ⑥ ( 贝塞尔曲线递归算法原理 | 贝塞尔曲线递归算法实现 ) ;


为贝塞尔曲线控制点填充数据 : 三阶贝塞尔曲线 , 需要设置一个 起始点 , 一个终止点 , 和 两个控制点 ;

        // 起始点 + 控制点 + 终止点
        mControlPoints = new ArrayList<>();
        // 三阶贝塞尔曲线加入 起始点 + 2 个控制点 + 终止点
        mControlPoints.add(new PointF(0, getHeight() / 2F));            // 起始点
        mControlPoints.add(new PointF(getWidth() / 4F, getHeight()));      // 控制点 1
        mControlPoints.add(new PointF(getWidth() * 3F / 4F, 0));        // 控制点 2
        mControlPoints.add(new PointF(getWidth(), getHeight() / 2F));      // 终止点

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    •




二、代码示例


使用 德卡斯特里奥算法 公式计算的 方法绘制三阶贝塞尔曲线示例 :

package kim.hsl.paintgradient.bezier;

import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.View;
import androidx.annotation.Nullable;

import java.util.ArrayList;

public class BesselCurve3 extends View {

    // 贝塞尔曲线绘制画笔
    private Paint mPaint;

    // 贝塞尔曲线
    private Path mPath;

    // 贝塞尔曲线控制点集合
    private ArrayList<PointF> mControlPoints = new ArrayList<>();

    public BesselCurve3(Context context) {
        this(context, null);
    }

    public BesselCurve3(Context context, @Nullable AttributeSet attrs) {
        this(context, attrs, 0);
    }

    public BesselCurve3(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
    }

    @Override
    protected void onSizeChanged(int width, int height, int oldWidth, int oldHeight) {
        super.onSizeChanged(width, height, oldWidth, oldHeight);

        // 初始化 曲线 和 画笔 实例对象\
        mPaint = new Paint();
        mPaint.setColor(Color.BLACK);
        mPaint.setStyle(Paint.Style.STROKE);
        mPaint.setStrokeWidth(5);

        // 贝塞尔曲线
        mPath = new Path();

        // 起始点 + 控制点 + 终止点
        mControlPoints = new ArrayList<>();
        // 三阶贝塞尔曲线加入 起始点 + 2 个控制点 + 终止点
        mControlPoints.add(new PointF(0, getHeight() / 2F));            // 起始点
        mControlPoints.add(new PointF(getWidth() / 4F, getHeight()));      // 控制点 1
        mControlPoints.add(new PointF(getWidth() * 3F / 4F, 0));        // 控制点 2
        mControlPoints.add(new PointF(getWidth(), getHeight() / 2F));      // 终止点
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);

        // 使用 Path 实例对象存放贝塞尔曲线上的点集
        mPath.reset();

        // 用于存放贝塞尔曲线上点的集合
        ArrayList<PointF> points = new ArrayList<>();

        // 计算阶数 , 点的个数减去一 , 就是阶数 ;
        // 一阶贝塞尔曲线有 2 个点
        // 二阶贝塞尔曲线有 3 个点
        // n - 1 阶贝塞尔曲线有 n 个点
        int order = mControlPoints.size() - 1;

        // 贝塞尔曲线由 1000 个点组成 , 也就是 比例 u 每次增加 0.001
        // 贝塞尔曲线上的点的集合中收集 1000 个点
        float delta = 1.0f / 1000;

        // 每次累加 0.0001
        for (float u = 0; u <= 1; u += delta) {
            // Bezier点集
            PointF pointF = new PointF(BezierX(order, 0, u), BezierY(order, 0, u));
            points.add(pointF);
            if(points.size() == 1){
                mPath.moveTo(points.get(0).x,points.get(0).y);
            }else{
                mPath.lineTo(pointF.x,pointF.y);
            }
        }

        // 绘制贝塞尔曲线
        canvas.drawPath(mPath,mPaint);
    }

    /**
     * 贝塞尔曲线递归算法, 本方法计算 X 轴坐标值
     * @param i 贝塞尔曲线阶数 3
     * @param j 贝塞尔曲线控制点, 设置 0 即可, 3 阶曲线 依赖于 第 0 个二阶曲线和第 1 个二阶曲线
     * @param u 比例 / 时间 , 取值范围 0.0 ~ 1.0
     * @return
     */
    private float BezierX(int i, int j, float u) {
        if (i == 1) {
            // 递归退出条件 : 贝塞尔曲线阶数 降为一阶
            // 一阶贝塞尔曲线点坐标 计算如下 :
            return (1 - u) * mControlPoints.get(j).x + u * mControlPoints.get(j + 1).x;
        }
        return (1 - u) * BezierX(i - 1, j, u) + u * BezierX(i - 1, j + 1, u);
    }

    /**
     * 贝塞尔曲线递归算法, 本方法计算 Y 轴坐标值
     * @param i 贝塞尔曲线阶数
     * @param j 贝塞尔曲线控制点
     * @param u 比例 / 时间 , 取值范围 0.0 ~ 1.0
     * @return
     */
    private float BezierY(int i, int j, float u) {
        if (i == 1) {
            // 递归退出条件 : 贝塞尔曲线阶数 降为一阶
            return (1 - u) * mControlPoints.get(j).y + u * mControlPoints.get(j + 1).y;
        }
        return (1 - u) * BezierY(i - 1, j, u) + u * BezierY(i - 1, j + 1, u);
    }
}

  
 

  
 

 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    • 
  
  • 69
    • 
  
  • 70
    • 
  
  • 71
    • 
  
  • 72
    • 
  
  • 73
    • 
  
  • 74
    • 
  
  • 75
    • 
  
  • 76
    • 
  
  • 77
    • 
  
  • 78
    • 
  
  • 79
    • 
  
  • 80
    • 
  
  • 81
    • 
  
  • 82
    • 
  
  • 83
    • 
  
  • 84
    • 
  
  • 85
    • 
  
  • 86
    • 
  
  • 87
    • 
  
  • 88
    • 
  
  • 89
    • 
  
  • 90
    • 
  
  • 91
    • 
  
  • 92
    • 
  
  • 93
    • 
  
  • 94
    • 
  
  • 95
    • 
  
  • 96
    • 
  
  • 97
    • 
  
  • 98
    • 
  
  • 99
    • 
  
  • 100
    • 
  
  • 101
    • 
  
  • 102
    • 
  
  • 103
    • 
  
  • 104
    • 
  
  • 105
    • 
  
  • 106
    • 
  
  • 107
    • 
  
  • 108
    • 
  
  • 109
    • 
  
  • 110
    • 
  
  • 111
    • 
  
  • 112
    • 
  
  • 113
    • 
  
  • 114
    • 
  
  • 115
    • 
  
  • 116
    • 
  
  • 117
    • 
  
  • 118
    • 
  
  • 119
    • 
  
  • 120
    • 
  
  • 121
    • 
  
  • 122
    • 
  
  • 123
    • 
  
  • 124
    • 
  
  • 125
    • 
  
  • 126
    •

三阶贝塞尔曲线绘制效果 :

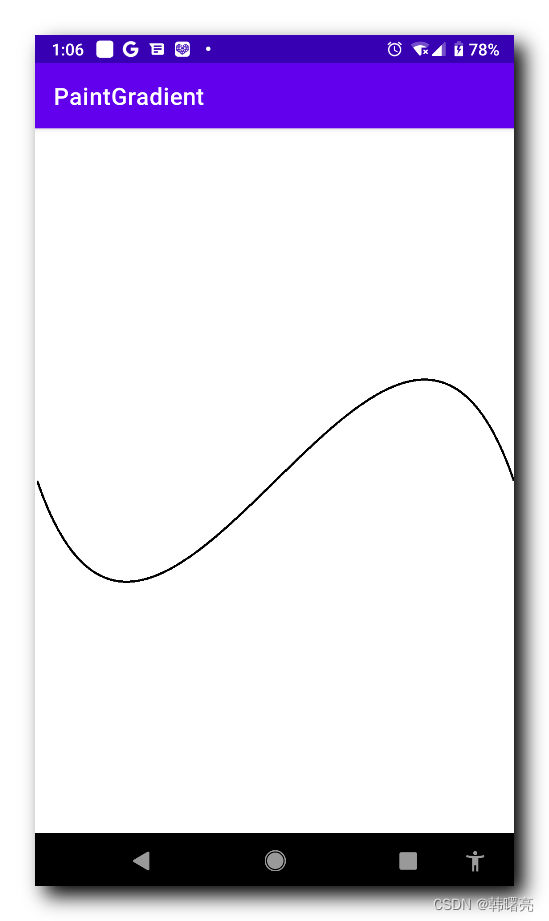
在这里插入图片描述

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/126127888

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
Android
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入