【单目标优化求解】基于matlab贪婪非分级灰狼算法求解单目标优化问题（G-NHGWO）【含Matlab源码 2005期】

一、贪婪随机自适应搜索算法简介

1 贪婪随机自适应搜索算法
GRASP算法分两个阶段，构造阶段和局部搜索阶段[3]。在构造阶段，初始化可行解S和候选集C，并对候选集的每一个元素进行评估，判断是否可加入限制候选列表（Restricted Candidate List, RCL）。每次从RCL中随机选取一个值与可行解S进行比对，更新RCL的元素，并对包含的所有元素进行再次评估，直到满足条件时结束。

RCL规模大小也会影响此算法性能，规模过大会生成很多差别的解。RCL通常采用静态固定法和动态调整法来调整列表规模，体现了GRASP算法自适应功能。

在第一阶段会得到质量不高的可行解，因此在第二阶段，可行解需要以持续不断的迭代方式进行局部搜索，以求得最优解。若局部新优解S比目前的优解S更优的话，就更换S，直到找到最优解。选择相邻解在局部搜索阶段有两种方法：最优适应和首次适应。最优适应在所有相邻解被搜寻后，将更优相邻解替换为可行解；首次适应是当搜索到比可行解更优相邻解时进行替换后再次局部搜索，当循环达到满足给定的迭代次数时终止。

2 灰狼优化算法
GWO算法模仿灰狼的社会等级制度和猎食行为，并控制搜索方位。灰狼优化算法已被广泛应用并不断改进，主要体现在约束函数优化、多级阈值图像分割、路径优化等领域。灰狼等级从高到低为α，β，δ，ω这四种等级，每一个等级表示一个可能解。α狼是狼群头领，拥有最高决策权，代表最优解；β，δ，ω狼分别代表优解、次优解、候选解。狼群每次捕猎过程是由各等级的相互协作完成，由搜寻、包围、攻击3个步骤组成。

2.1 搜寻过程
该算法通过随机数扰乱判断与猎物之间的距离，以此初始化种群。

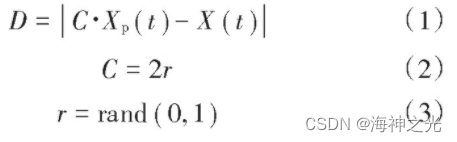
式中：t为当下迭代次数；X (t）为灰狼的位置；Xp (t）为第t次迭代中猎物位置；D为灰狼与猎物的间距；r为0～1之间的任意随机数。

2.2 包围过程
在灰狼包围猎物的过程中，通过狼之间不同距离和猎物距离，建立灰狼与猎物的关系模型。

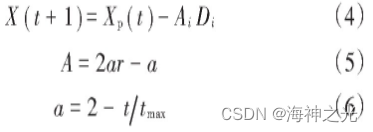
式中：A表示包围步长；tmax表示最大迭代次数，控制参数a随着算法迭代次数的增加而线性递减。其中，当|A|≥1时，表示灰狼会进行全局搜索；而|A|<1时，意味灰狼将在附近搜索。A, C的随机初始化保证了灰狼在搜索过程中易达到全局最优位置。

2.3 位置更新（攻击）
通过α，β，δ，ω更新位置信息，判断目标猎物位置并对猎物攻击。产生新位置关系后，对狼群中的元素进行边界控制，完成一次迭代。此阶段狼群位置更新如图1所示。

式中：X1, X2, X3表示α，β，δ狼的位置；A1, A2, A3表示3个随机数；X表示灰狼攻击猎物的最终位置。灰狼通过速度变异、搜索半径变化、位置更新等策略，并借助参数A和C的随机变化、较强的全局能力，使得灰狼在全局范围亦可搜寻到最优解或次最优解。重复进行上述步骤，直到达到终止条件输出最优解。综述，灰狼捕食过程是可以抽象成连续空间上的组合优化模型。

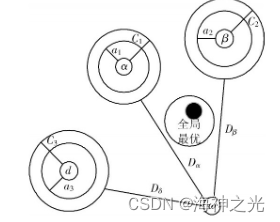
图1 GWO算法中灰狼位置更新图

二、部分源代码

clear

global NFE
NFE=0;

nPop=30;    % Number of search agents (Population Number)
MaxIt=1000; % Maximum number of iterations
nVar=30;    % Number of Optimization Variables

nFun=1;     % Function No, select any integer number from 1 to 14

CostFunction=@(x,nFun) Cost(x,nFun);        % Cost Function

%% Problem Definition

VarMin=-100;             % Decision Variables Lower Bound
if nFun==7
    VarMin=-600;             % Decision Variables Lower Bound
end
if nFun==8
    VarMin=-32;             % Decision Variables Lower Bound
end
if nFun==9
    VarMin=-5;             % Decision Variables Lower Bound
end
if nFun==10
    VarMin=-5;             % Decision Variables Lower Bound
end
if nFun==11
    VarMin=-0.5;             % Decision Variables Lower Bound
end
if nFun==12
    VarMin=-pi;             % Decision Variables Lower Bound
end
if nFun==14
    VarMin=-100;             % Decision Variables Lower Bound
end
VarMax= -VarMin;             % Decision Variables Upper Bound
if nFun==13
    VarMin=-3;             % Decision Variables Lower Bound
    VarMax= 1;             % Decision Variables Upper Bound
end

%%   NH-Grey Wold Optimizer (GWO)

% Initialize Best Solution (Alpha) which will be used for archiving
Alpha_pos=zeros(1,nVar);
Alpha_score=inf;

%Initialize the positions of search agents
Positions=rand(nPop,nVar).*(VarMax-VarMin)+VarMin;
Positions1=rand(nPop,nVar).*(VarMax-VarMin)+VarMin;
BestCosts=zeros(1,MaxIt);

fitness(1:nPop)=inf;
fitness1=fitness;

iter=0;  % Loop counter

%% Main loop
while iter<MaxIt
    for i=1:nPop
        
        % Return back the search agents that go beyond the boundaries of the search space
        Flag4ub=Positions1(i,:)>VarMax;
        Flag4lb=Positions1(i,:)<VarMin;
        Positions1(i,:)=(Positions1(i,:).*(~(Flag4ub+Flag4lb)))+VarMax.*Flag4ub+VarMin.*Flag4lb;
        
        % Calculate objective function for each search agent
        fitness1(i)= CostFunction(Positions1(i,:), nFun);
        
        % Update Grey Wolves
        if fitness1(i)<fitness(i)
            Positions(i,:)=Positions1(i,:);
            fitness(i) =fitness1(i) ;
        end
        
        % Update Best Solution (Alpha) for archiving
        if fitness(i)<Alpha_score
            Alpha_score=fitness(i);
            Alpha_pos=Positions(i,:);
        end
        
    end
    

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 高珊,孟亮.贪婪随机自适应灰狼优化算法求解TSP问题[J].现代电子技术. 2019,42(14)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/126085746