⭐️前面的话⭐️

本篇文章介绍来自牛客试题广场的两道题题解，分别为【把字符串转换成整数】和【不要二】，展示语言java。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创！
📆首发时间：🌴2022年7月31日🌴
✉️坚持和努力一定能换来诗与远方！
💭推荐书籍：📚《数据结构与算法》，📚《算法导论》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

⭐️把字符串转换成整数⭐️

🔐题目详情

将一个字符串转换成一个整数，要求不能使用字符串转换整数的库函数。 数值为 0 或者字符串不是一个合法的数值则返回 0

数据范围：字符串长度满足 $0≤n≤100$
进阶：空间复杂度 O(1) ，时间复杂度 O(n)

注意：

①字符串中可能出现任意符号，出现除 +/- 以外符号时直接输出 0

②字符串中可能出现 +/- 且仅可能出现在字符串首位。

输入描述：

输入一个字符串,包括数字字母符号,可以为空

返回值描述：

如果是合法的数值表达则返回该数字，否则返回0

示例1

输入：

"+2147483647"

返回值：

2147483647

示例2

输入：

"1a33"

返回值：

0

题目链接：把字符串转换成整数

💡解题思路

基本思路： 模拟
解题思路1：
我们来看看题，它说让我们将字符串转换为整数，并且不能使用库函数，emmm，它说不能用你就不用？我偏要用!所以第一种思路就是使用库函数，这个就不多说了。

解题思路2：

特殊的一种情况，判断字符串的第一个字符时，如果为-，我们可以设计一个标记isPos表示这个数是不是正数，如果不是，将isPos设置为false，反之为true，如果为+不用处理，如果为其他非数字字符，返回0即可。

对于字符串上其他的字符，直接判断是不是数字，即判断字符的大小是否介于['0', '9']之间，如果不满足，直接返回0。

🔑源代码

解题思路2：

import java.util.*;
public class Solution {
    public int StrToInt(String str) {
        char[] cs = str.toCharArray();
        int n = cs.length;
        int ans = 0;
        boolean isPos = true;
        
        for (int i = 0; i < n; i++) {
            char c = cs[i];
            if (c > '0' && c < '9') {
                ans = ans * 10 + (c - '0');
            } else if (i == 0 && c == '-') {
                isPos = false;
                continue;
            } else if (i == 0 && c == '+') {
                continue;
            } else {
                return 0;
            }
        }
        //不是正数
        if (!isPos) {
            ans = -ans;
        }
        return ans;
    }
}

🌱总结

本题为字符串模拟题，本质上就是判断一个字符是不是数字。

⭐️不要二⭐️

🔐题目详情

二货小易有一个W*H的网格盒子，网格的行编号为0 ~ H-1，网格的列编号为0 ~ W-1。每个格子至多可以放一块蛋糕，任意两块蛋糕的欧几里得距离不能等于2。
对于两个格子坐标(x1,y1),(x2,y2)的欧几里得距离为:
$( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) )$ 的算术平方根
小易想知道最多可以放多少块蛋糕在网格盒子里。

输入描述：

每组数组包含网格长宽W,H，用空格分割.(1 ≤ W、H ≤ 1000)

输出描述：

输出一个最多可以放的蛋糕数

示例1

输入：

3 2

输出：

4

题目链接：不要二

💡解题思路

基本思路： 数学推理

解题思路： 这道题从题面上看，感觉是网易的一道笔试题，不管那么多了，我们来进行分析，任意两块蛋糕的距离不能等于2，根据题目所给的距离计算公式我们可以得到以下等式： $( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) )\ !=\ 4$。
由于题目给定的坐标不会是小数，因此如果上述式子成立，那么 $(x1-x2) * (x1-x2)$ 与 $(y1-y2) * (y1-y2)$一定也是整数，那这就好办了，我们先把结果 $4$拆分：
$4 = 1+3$
$4=3+1$
$4=2+2$
$4=0+4$
$4=4+0$
也就这几种情况而已，我们再来分析分析，容易知道 $(x1-x2)$ 与 $(y1-y2)$为整数，因此 $(x1-x2) * (x1-x2)$ 与 $(y1-y2) * (y1-y2)$一定是某一个整数的平方，所以前三种情况是不可能的，因此只剩下：
$4=0+4$
$4=4+0$
即 $(x1-x2) * (x1-x2)$ 不为 $4$或 $0$, $(y1-y2) * (y1-y2)$ 不为 $4$或 $0$，即 $(x1-x2) != 2\ \&\&\ (y1-y2) != 0$或者 $(x1-x2) != 0\ \&\&\ (y1-y2) != 2$，当满足此条件时对应的网格才可以放蛋糕。

我们可以来定义一个大小为h*w的二维数组来表示对应位置能不能放置蛋糕，如果能，对应位置置为0，否则置为1，首先，创建一个二维数组，并将所有的元素都置为0，表示能放置蛋糕，我们以从左到右，从上到下的顺序遍历该二维数组，如果遍历结果的值为0，计数器加1，并将下方向(i+2, j)与右方向(i, j+2)位置置为1，因为我们就是以向右与向下方向遍历的，所以修改右边与下边的网格结果即可，当然你想把四周的网格都改掉也可以，但是没有必要。

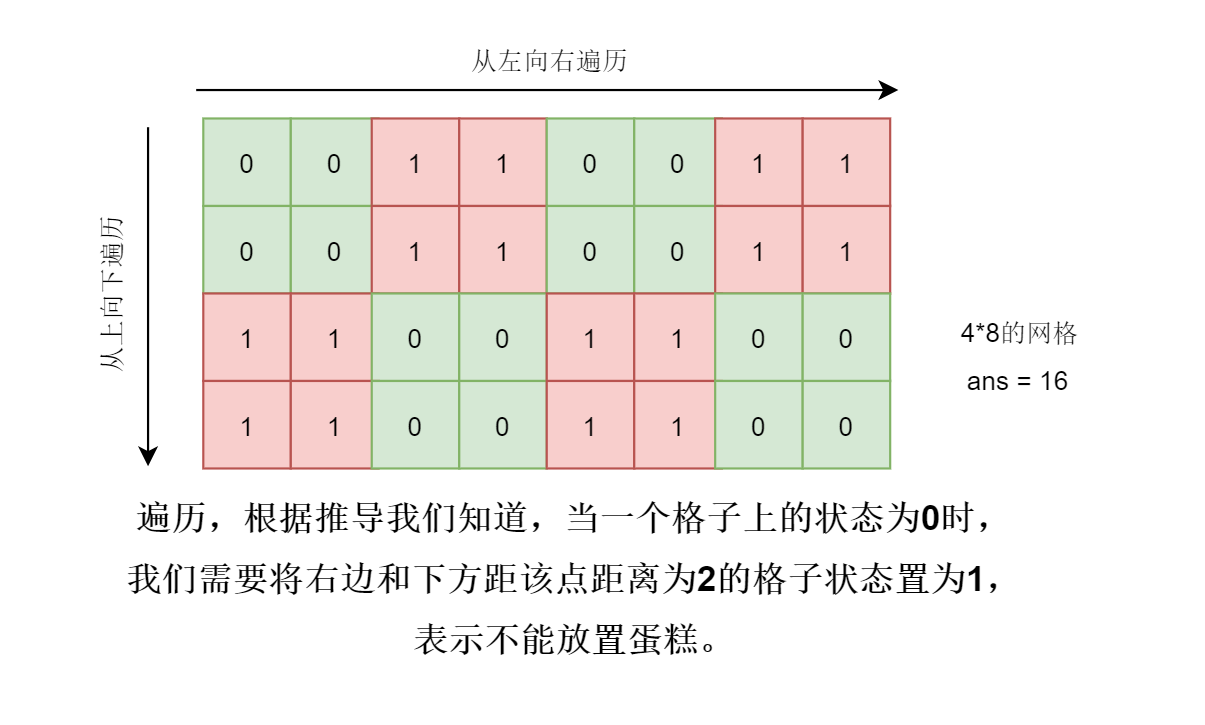
🔑源代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int w = sc.nextInt();
        int h = sc.nextInt();
        
        //标记,为0表示放置蛋糕，非0表示不放置蛋糕
        int[][] f = new int[h][w];
        int ans = 0;
        for (int i = 0; i < h; i++) {
            for (int j = 0; j < w; j++) {
                if (f[i][j] == 0) {
                    ans++;
                    //更新距离为2的位置为1
                    if (i + 2 < h) {
                        f[i + 2][j] = 1;
                    } 
                    if (j + 2 < w) {
                        f[i][j + 2] = 1;
                    }
                }
            }
        }
        System.out.println(ans);
    }
}

🌱总结

本题属于数学推理题，推导出不能放蛋糕的坐标关系时，我们可以先建立一个W*H二维数组，设状态0表示能放蛋糕，初始时所有网格都标记为可以放蛋糕，然后我们遍历数组，按照不能放蛋糕的坐标条件来将不满足放蛋糕的位置标记为1，最后我们在遍历过程中实时计算可以放蛋糕的格数即可。