神奇的数据——树形结构

树

1. 树和二叉树

1.1 什么是树

树（tree）是n（n>=0）个节点的有限集。当n=0时，称为空树。在任意一个非空树中存在以下特点：

1. 有且仅有一个特定的点称为根节点。

2. 当n>1时其余的节点可分为m个互不相交的有限集，每一个集合本身又是一个树，并称为根的子树。

1.1.1 名词：

• 根节点（root）：顶端没有“父亲”，称为根节点。
• 叶子节点（leaf）：末端没有“孩子”，称为叶子节点。
• 父节点（parent）：节点的上一级。
• 孩子节点（child） ：节点的下一级。
• 兄弟节点（sibling）：同级节点。

1.2 什么是二叉树

• 二叉树：每个节点最多有两个孩子节点。最多有两个，可能只有一个孩子节点或者没有。
• 满二叉树：一个二叉树的所有非叶子节点都存在左右孩子， 并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。
• 完全二叉树：对一个有n个节点的二叉树， 按层级顺序编号， 则所有节点的编号为从1到n。 如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同， 则这个二叉树为完全二叉树。
• 完全二叉树的条件没有满二叉树那么苛刻： 满二叉树要求所有分支都是满的； 而完全二叉树只需保证最后一个节点之前的节点都齐全即可。

1.3 物理存储结构

1. 链式存储结构：

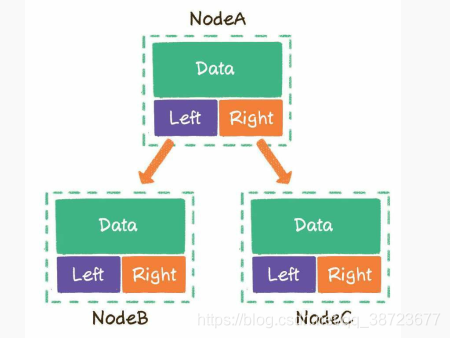
二叉树的每一个节点包含3个部分：

• 存储数据的data变量
• 指向左孩子的left指针
• 指向右孩子的right指针

2. 数组：

使用数组存储时， 会按照层级顺序把二叉树的节点放到数组中对应的位置上。 如果某一个节点的左孩子或右孩子空缺， 则数组的相应位置也空出来。

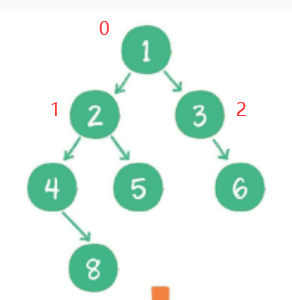
• 父节点下标是parent，那么左孩子是2*parent+1，右孩字是2*parent+2。

1.4 二叉树的应用

二叉树最主要的应用还在于进行查找操作和维持相对顺序这两个方面。

1.4.1 查找

二叉树的树形结构使他很适合扮演索引的角色。

二叉查找树（ binary search tree）：二叉查找树在二叉树的基础上增加了以下几个条件

• 如果左子树不为空， 则左子树上所有节点的值均小于根节点的值
• 如果右子树不为空， 则右子树上所有节点的值均大于根节点的值
• 左、 右子树也都是二叉查找树

对于一个节点分布相对均衡的二叉查找树来说， 如果节点总数是n， 那么搜索节点的时间复杂度就是O(logn)， 和树的深度是一样的。

1.4.2 维持相对顺序

二叉查找树要求左子树小于父节点，右子树大于父节点，正是这样保证了二叉树的有序性。

因此二叉查找树还有另一个名字—二叉排序树。

新插入的节点同样要遵循二叉排序树的原则。

在二叉查找树中依次插入9、 8、 7、 6、 5、 4 二叉树会变成一个跛脚的二叉树，解决这个问题就涉及到二叉树的自平衡了。二叉树自平衡的方式有多种，如红黑树、AVL树、树堆等。

除二叉查找树以外， 二叉堆也维持着相对的顺序。

2. 二叉树的遍历

二叉树的遍历分为4种：

• 前序遍历。
• 中序遍历。
• 后序遍历。
• 层序遍历。

从更宏观的角度来看，二叉树的遍历归结为两大类。

• 深度优先遍历（前序遍历，中序遍历，后序遍历）。
• 广度优先遍历（层序遍历）。

2.1 深度优先遍历

2.1.1 前序遍历

递归先输出，再递归左孩子，再递归右孩子。

2.1.2 中序遍历

先递归左孩子，输出，递归右孩子。

2.1.3 后序遍历

先递归左孩子，再递归右孩子，输出。

2.2 广度优先遍历

使用队列

3. 什么是二叉堆

3.1 初始二叉堆

二叉堆本质上是一种完全二叉树，它分为两个类型

1. 最大堆：任何一个父节点都大于或等于他的左孩子、右孩子节点的值。
2. 最小堆：任何一个父节点都小于或等于他的左孩子、右孩子节点的值。

二叉堆的根节点叫做栈顶。

最大堆和最小堆的特点决定了：最大堆的堆顶是整个堆中的最大元素；最小堆的堆顶是整个堆中的最小元素。

3.2 二叉堆的自我调整

对于二叉堆，有如下几种操作

1. 插入节点：

   当二叉堆插入节点时。插入位置是完全二叉树的最后一个位置，然后与父节点比较交换位置即可。

2. 删除节点：

   删除一个节点，使得最后一个节点放到被删除的位置，然后同左右孩子进行比较，移动。

3. 构建二叉堆：

   把一个无序的二叉树调整为二叉堆，本质就是让所”非叶子“节点“下沉”。

   如构建最小堆

从最后一个非叶子节点开始，即10，与左右孩子中最小的一个比较，如果大于它，“下沉”交换位置。

3.3 二叉堆的代码实现

4. 什么是优先队列

4.1优先队列的特点

1. 队列的特点：先进先出。
2. 最大优先队列：无论当前顺序如何，总是当前最大元素优先出队。
3. 最小优先队列：无论当前顺序如何，总是当前最小元素优先出队。

4.2 优先队列的实现

1. 最大堆的堆顶是整个堆中的最大元素。
2. 最小堆的堆顶是整个堆中的最小元素。

5. 小结

1. 什么是树

   树是n个节点的有限集，有且仅有一个特定的称为根节点。当n>1时，其余节点可以分为m个互不相交的有限集，每个集合本身又是一个树，并称为根的子树。

2. 什么是二叉树

   二叉树是树的一种特殊形式，每个节点最多有两个孩子节点。二叉树包括完全二叉树和满二叉树两种特殊形式。

3. 二叉树的遍历方式有几种

   根据遍历节点之间的关系，可以分为前序遍历、中序遍历、后续遍历、层序遍历这四种方式；从更宏观的角度划分，可以划分为深度优先遍历和广度优先遍历。

4. 什么是二叉堆

   二叉堆是一种特殊的二叉树，分为最大堆和最小堆

   在最大堆中任何一个子节点的值都小于父节点。

   在最小堆中任何一个子节点的值都大于父节点。

5. 什么是优先队列

   优先队列分为最大优先队列和最小优先队列。

   在最大优先队列中，无论入场顺序如何，当前最大的元素会优先出队，这是基于最大堆实现的。

   在最小优先队列中，无论入场顺序如何，当前最小的元素会优先出队，这是基于最小堆实现的。