贝塞尔曲线参考 : https://github.com/venshine/BezierMaker

一、一阶贝塞尔曲线

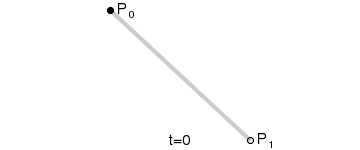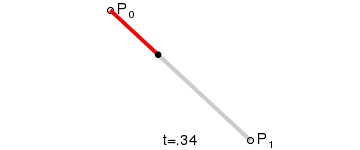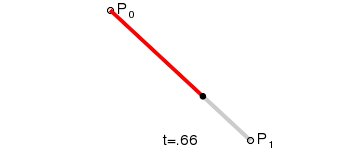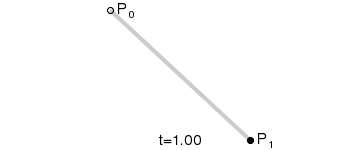
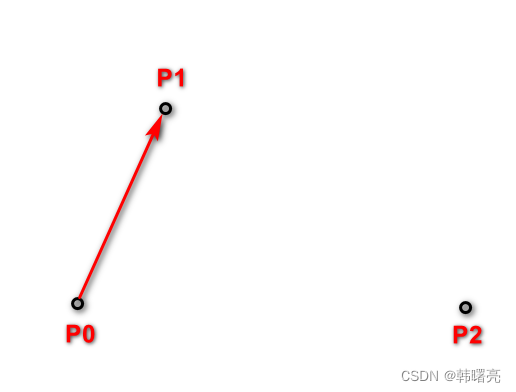
一阶贝塞尔曲线 本质 是一条直线 , 下图是 一阶贝塞尔曲线 , $P_0$ 是曲线开始位置 , 逐个点向 $P_1$ 绘制 ;

二、二阶贝塞尔曲线

二阶贝塞尔曲线 需要在 一阶贝塞尔曲线 基础上 , 添加一个控制点 , 曲线的绘制受控制点影响 ;

下图中 由 $P_0$ 向 $P_2$ 绘制 二阶贝塞尔曲线 , 控制点是 $P_1$ ;

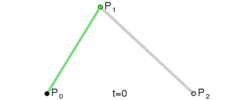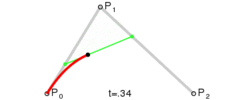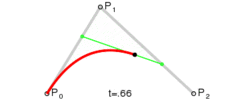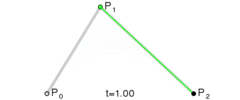
由 $P_0$ 点绘制一条曲线到 $P_2$ 点 , 绘制该曲线时 , 有一个控制点 $P_0$ , 相当于 将曲线向 " 控制点 $P_0$ " 方向拖动 , 产生一条圆滑的弧线 ;

上述绘制的 弧线 , 是通过计算得来的 , 绘制 $P_0$ 到 $P_2$ 的弧线 , 中间引入一个控制点 $P_1$ ,

• 首先由 起始点 $P_0$ 与 控制点 $P_1$ 进行连线 ,
  

• 然后由 控制点 $P_1$ 与 结束点 $P_2$ 进行连线 ,

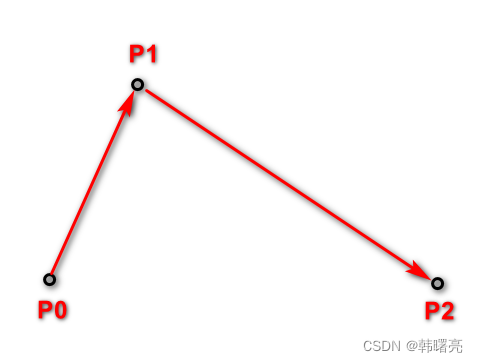
• $P_0$ 到 $P_1$ 可以认为是 一阶贝塞尔曲线 , $P_1$ 到 $P_2$ 也可以认为是 一阶贝塞尔曲线 ,
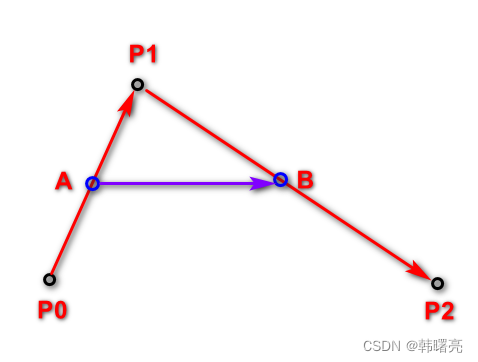
• 由 起始点 $P_0$ 与 控制点 $P_1$ 连线的这条线开始进行控制 ,
• 在 起始点 $P_0$ 与 控制点 $P_1$ 连线上找到一个 比例值 $x$ ( 取值范围 $0-1.0$ ) , 找到 $x$ 比例所处的点 $A$ , 同时在 控制点 $P_1$ 与 结束点 $P_2$ 连线上 , 找到一个 比例值 $x$ 对应的点 $B$ , 将 $AB$ 两个点进行连线 ,

• 贝塞尔曲线上绘制的点 , 是 在 $AB$ 连线上的 $x$ 比例所在位置 , 绿色的点 $C$ 就是贝塞尔曲线要绘制的位置 ;

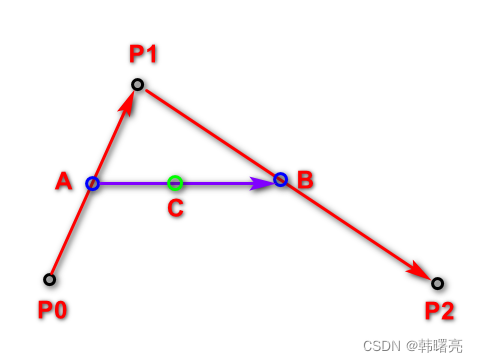
上述计算过程中的比例 :

$$\frac{P_{0}A}{P_0{P}_1}=\frac{P_{1}B}{P_1{P}_2}=\frac{AC}{AB}$$

其中 $P_{0}A$ 表示 $P_0$ 点到 $A$ 点的线段长度 , $P_0{P}_1$ 表示 $P_0$ 点到 $P_1$ 点的线段长度 ;

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/125769728