科学计算工具包SciPy傅里叶变换

导读

关于傅里叶变换想必大家应该都不陌生吧？在信号处理以及高等数学等都有它的身影，关于它说的最多的一句话就是将信号在时域和频域中进行变换，对于这句话大家也许都是似懂非懂。通过这篇文章，你将能够学到一下几点：

1. 什么是傅里叶变换，为什么需要它？
2. 傅里叶变换的应用有哪些
3. 如何使用scipy来使用傅里叶变换

傅里叶变换

傅里叶变换(Fourier Transform)：是一种线性积分变换，用于在时域(或空域)和频域之间的变换，在物理学和工程学中应用甚广。傅里叶变换是一个非常强大的信号分析工具，它能够用于音频型号的处理、图片压缩、去噪。

• 傅里叶变换的应用

将音频文件通过傅里叶变换来实现歌曲识别，通过傅里叶变换可以实现图片的压缩，将图片数据转换为频域数据，移除高频部分来实现图片的压缩，语音识别利用傅里叶变换和相关的变换从原始的音频信号中恢复语音。

很多时候对于一些在时域变化很复杂的信号，我们很难分析出它的特征和有用信息时，可以通过傅里叶变换将其转换到频域，通过分析频率以及振幅的变化来寻找有用信息。

• scipy中傅里叶变换的使用

scipy的fft模块提供了许多的傅里叶变换工具，接下来我们将介绍如何来使用它

scipy傅里叶变换的使用

下面我们通过几个实例来说明，如何应用scipy中的傅里叶变换

移除信号中的噪声

• 生成虚拟信号
  我们定义一个函数generate_audio_wave用来产生一段原始的音频信号

from scipy import fft
import numpy as np
from matplotlib import pyplot as plt

def generate_audio_wave(freq,sample_rate,duration):
    """产生一段虚拟的音频信号
    :param freq: 信号的频率
    :param sample_rate: 信号的采样率
    :param duration: 信号采样的时长
    :return:
    """
    #生成一段时间序列
    t = np.linspace(0,duration,sample_rate*duration,endpoint=False)
    #设置产生音频信号的频率
    frequencies = t * freq
    #设置音频信号的输出的幅值
    y = np.sin((2 * np.pi) * frequencies)
    return t,y


#设置生成音频的采样率
#1s产生44100个信号
SAMPLE_RATE = 44100
#设置生成音频时间的长度
DURATION = 5
t,y = generate_audio_wave(2,SAMPLE_RATE,DURATION)
plt.plot(t,y)
plt.show()

我们生成了一个，频率为2*44100,幅值为1时长为5s的正弦虚拟音频信号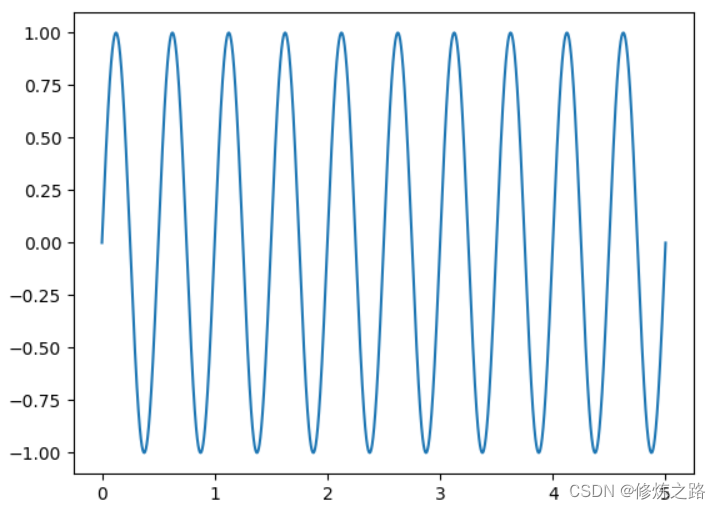

• 添加噪声
  我们模拟生成了两个信号，一个是原始的音频信号，一个是高频的噪声信号，然后将两个信号进行混合就产生了最终的信号，混合之后的信号由光滑的正弦波变成了带有许多毛刺信号的信号的正弦波

#设置生成音频的频率
#1s产生44100个信号
SAMPLE_RATE = 44100
#设置生成音频时间的长度
DURATION = 5
#生成音频信号
t,wav_signal = generate_audio_wave(400,SAMPLE_RATE,DURATION)
#模拟高频噪声
_,noise_signal = generate_audio_wave(4000,SAMPLE_RATE,DURATION)
#给音频信号添加高频噪声
mixed_signal = 0.3 * noise_signal + wav_signal
#展示添加高频噪声之后的波形图
plt.plot(mixed_signal[:1000])
plt.show()

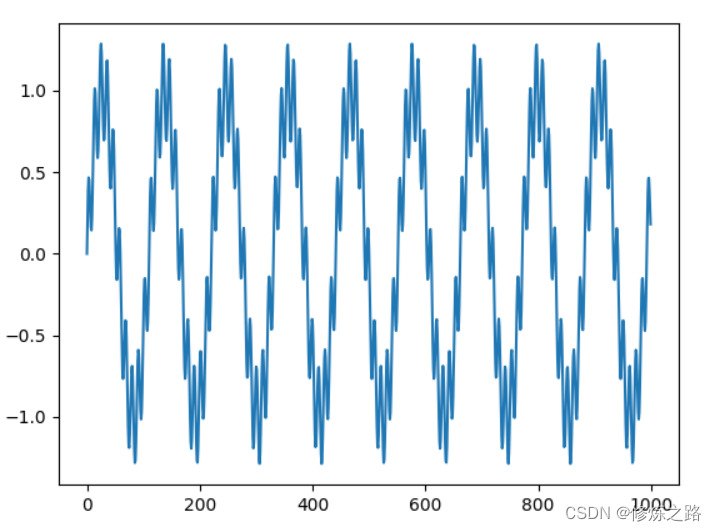
• 傅里叶变换
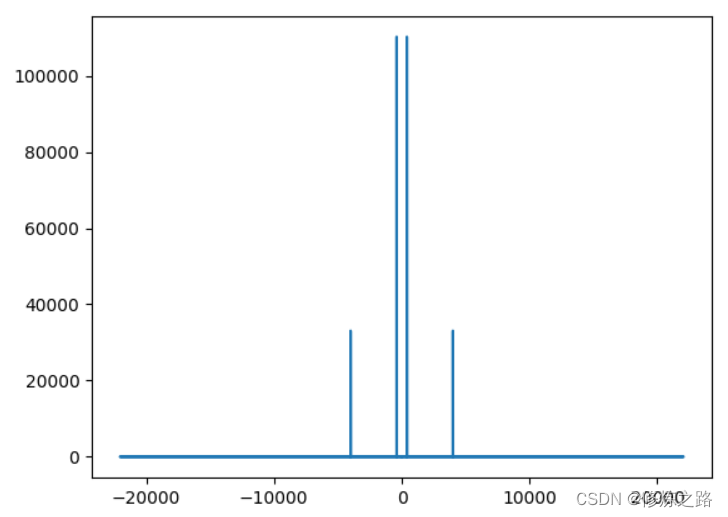
  我们使用傅里叶变换在合成的信号上，并且绘制出了合成信号的频谱图，发现x轴分为正负两个部分，而且对称，负正对称是傅里叶变换输入实值的一个副作用。通过分析频谱图发现，主要由两个频率的 信号组成，信号的频率是4000HZ和400HZ。分析幅值(y轴的值)发现，400HZ信号的频率要强于4000HZ的信号。

#计算采样的点数
N = SAMPLE_RATE*DURATION
#傅里叶变换
yf = fft.fft(mixed_signal)
#计算频率的中心,用来绘制x轴的数值
xf = fft.fftfreq(N,1 / SAMPLE_RATE)
#绘制频谱图
plt.plot(xf,np.abs(yf))
plt.show()

• 傅里叶逆变换去除噪声
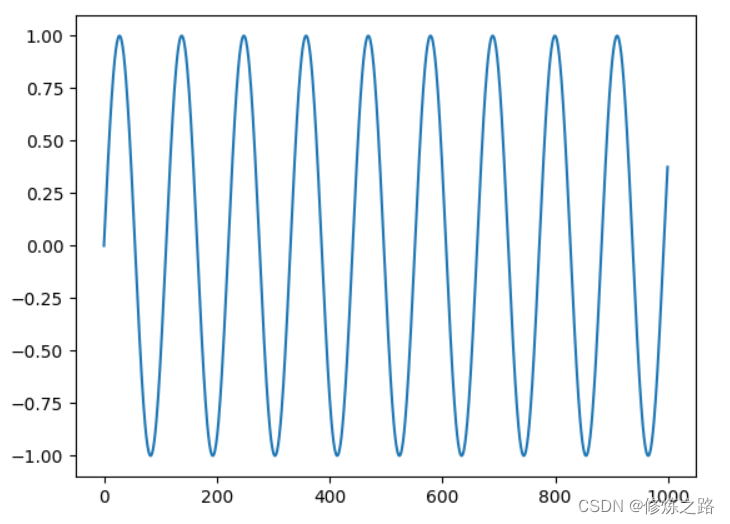
  我们先确定需要移除信号的频率，然后通过频率来找到信号的下标，在频域将信号清除之后，再通过傅里叶逆变换将频域的信号转换到时域信号，从而来实现噪声的移除。

#找到频率为4000HZ的索引
target_idx = np.squeeze(np.argwhere(np.abs(xf) == 4000))
#将4000HZ的信号清除
yf[target_idx] = 0
#傅里叶逆变换,还原去除噪声之后的信号
inv_yf = fft.ifft(yf)
#绘制信号
plt.plot(inv_yf[:1000])
plt.show()

参考

1. https://zh.wikipedia.org/wiki/%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2
2. https://docs.scipy.org/doc/scipy-1.8.0/html-scipyorg/tutorial/fft.html
3. https://www.youtube.com/watch?v=b06pFMIRO0I
4. https://realpython.com/python-scipy-fft/