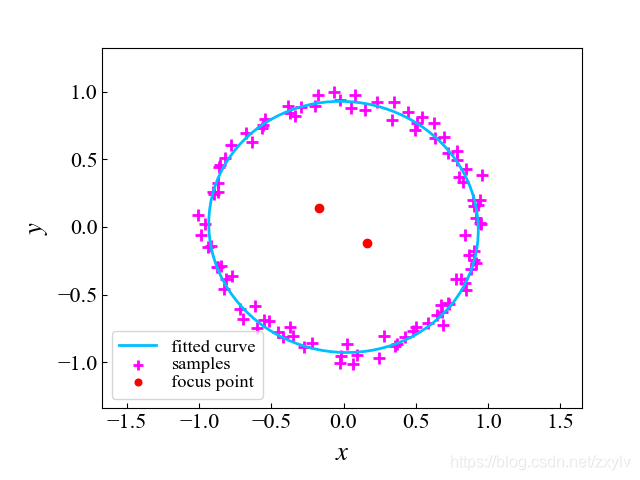
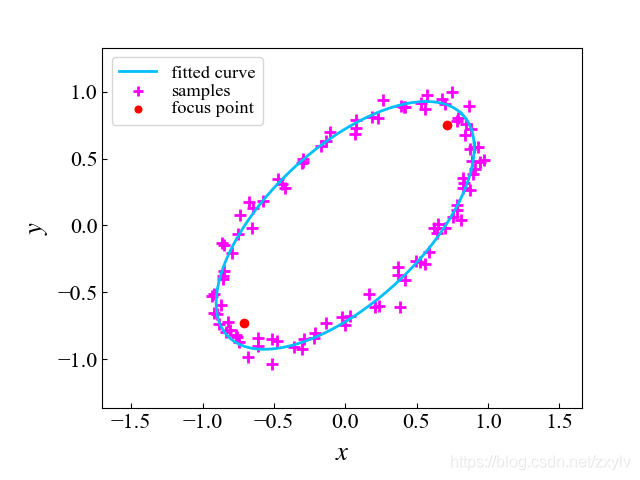
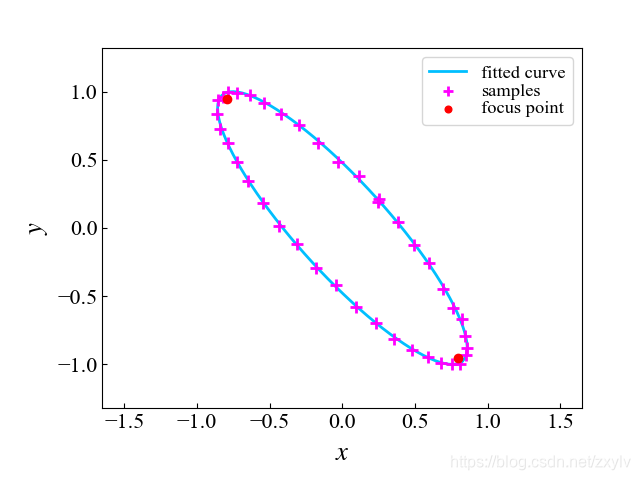
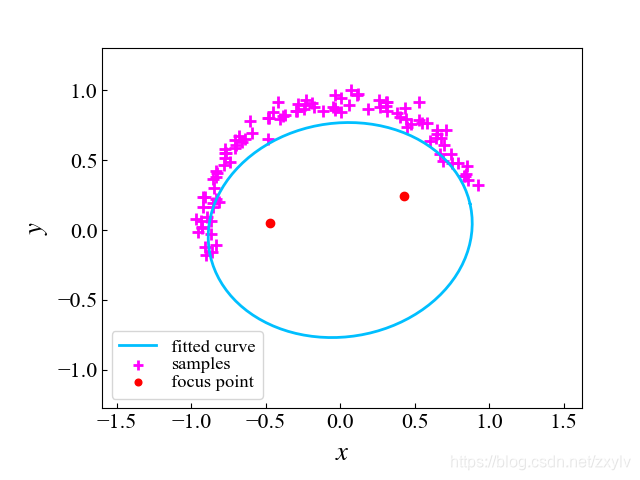
1.效果

2. 原理

椭圆有个性质：椭圆上的点到椭圆两焦点的距离之和为常数。
令：
1、椭圆上的点到两焦点的距离之和为 L t a r g e t L_{target} Ltarget​
2、两焦点坐标为 ( x f o c u s , 1   , y f o c u s , 1 ) , ( x f o c u s , 2   , y f o c u s , 2 ) (x_{focus,1}\,,y_{focus,1}),(x_{focus,2}\,,y_{focus,2}) (xfocus,1​,yfocus,1​),(xfocus,2​,yfocus,2​)
3、$n$个样本点坐标为： ( x s a m p l e s , i   , y s a m p l e s , i )    i = 1 , 2 , 3 , . . . , n (x_{samples,i}\,,y_{samples,i})\;i=1,2,3,...,n (xsamples,i​,ysamples,i​)i=1,2,3,...,n

则各样本点到椭圆两焦点的距离为：
L s a m p l e s , i = ( x s a m p l e s , i − x f o c u s , 1 ) 2 + ( y s a m p l e s , i − y f o c u s , 1 ) 2 + ( x s a m p l e s , i − x f o c u s , 2 ) 2 + ( y s a m p l e s , i − y f o c u s , 2 ) 2 L_{samples,i}= \sqrt{(x_{samples,i}-x_{focus,1})^2+(y_{samples,i}-y_{focus,1})^2} + \\\sqrt{(x_{samples,i}-x_{focus,2})^2+(y_{samples,i}-y_{focus,2})^2} Lsamples,i​=(xsamples,i​−xfocus,1​)2+(ysamples,i​−yfocus,1​)2 ​+(xsamples,i​−xfocus,2​)2+(ysamples,i​−yfocus,2​)2 ​
优化目标函数定义为 L s a m p l e s L_{samples} Lsamples​与 L t a r g e t L_{target} Ltarget​的方差：
I = ∑ i = 0 n ( L s a m p l e s , i − L t a r g e t ) 2 n − 1 I= \sqrt{\frac{\sum_{i=0}^n({L_{samples,i}-L_{target})^2}}{n-1}} I=n−1∑i=0n​(Lsamples,i​−Ltarget​)2​​
最后再使用任意方法（梯度下降，牛顿下山、狗腿等）对参数进行优化即可。此处使用了scipy的现成优化函数

scipy.optimize.minimize(fun, x0, args=())

具体使用方法参考scipy的api文档

3. 程序

import matplotlib.pyplot as plt
import scipy.optimize as so
import numpy as np

def my_fun(parameters, x_samples, y_samples):
    # 两焦点坐标以及椭圆上的点到两焦点的距离的和作为优化参数
    x_focus_1,y_focus_1,x_focus_2,y_focus_2,sum_of_target_distance_between_edge_and_two_focus = parameters
    # 计算实际距离
    sum_of_actual_distance_between_edge_and_two_focus= \
        ((x_samples- x_focus_1) ** 2 + (y_samples-y_focus_1) ** 2) ** 0.5+\
          ((x_samples- x_focus_2) ** 2 + (y_samples-y_focus_2) ** 2) ** 0.5

    # print(np.average(sum_of_actual_distance_between_edge_and_two_focus))
    # 返回方差
    return np.sum(((sum_of_actual_distance_between_edge_and_two_focus
                    - sum_of_target_distance_between_edge_and_two_focus) ** 2)/(len(x_samples)-1))

def fit_ellipse(x_samples, y_samples):
    # 归一化
    vmax= max(np.max(x_samples), np.max(y_samples))
    x_samples= x_samples / vmax
    y_samples= y_samples / vmax
    # 优化
    res_optimized = so.minimize(fun=my_fun, x0=np.array([-0.1,-0.05,0.1,0.1, 1.2]), args=(x_samples, y_samples))
    if res_optimized.success:
        print(res_optimized)
        x1_res, y1_res, x2_res, y2_res, l2_res = res_optimized.x
        # 依据优化得到的函数生成椭圆曲线
        # 计算椭圆偏角
        alpha_res= np.arctan((y2_res- y1_res)/(x2_res-x1_res))
        # 计算两焦点之间的距离
        l_ab= ((y2_res- y1_res)**2+ (x2_res-x1_res)**2)**0.5
        # 计算长（短）轴长度
        a_res= l2_res/2
        # 计算短（长）轴长度
        b_res=  ((l2_res/2)**2- (l_ab/2)**2)**0.5

        # 极坐标轴序列
        theta_res = np.linspace(0.0, 6.28, 100)
        # 生成椭圆上的点
        x_res = a_res * np.cos(theta_res) * np.cos(alpha_res) \
                - b_res * np.sin(theta_res) * np.sin(alpha_res)
        y_res = b_res * np.sin(theta_res) * np.cos(alpha_res) \
                + a_res * np.cos(theta_res) * np.sin(alpha_res)

        # plt.style.use("one")
        plt.axes([0.16, 0.15, 0.75, 0.75])
        plt.scatter(x_samples, y_samples, color="magenta", marker="+",
                    zorder=1, s=80, label="samples")
        plt.plot(x_res, y_res, color="deepskyblue", zorder=2,
                 label="fitted curve")
        plt.scatter(np.array([x1_res,x2_res]), np.array([y1_res,y2_res]),zorder=3,
                    color="r", label= "focus point")
        plt.xlabel("$x$")
        plt.ylabel("$y$")
        plt.legend()
        vmax = max(np.max(plt.xlim()), np.max(plt.ylim()))
        vmin = min(np.min(plt.xlim()), np.min(plt.ylim()))
        plt.ylim([1.1 * vmin - 0.1 * vmax, 1.1 * vmax - 0.1 * vmin])
        plt.xlim([1.25 * vmin - 0.25 * vmax, 1.25 * vmax - 0.25 * vmin])
        # plt.savefig("Figsave/a={:.3f};b={:.3f};theta={:.2f}deg.svg".format(a_res, b_res, alpha_res))
        plt.show()


if __name__== "__main__":
    theta_samples = np.linspace(0, 20, 100)
    # 椭圆方位角
    alpha_samples = -45.0 / 180.0 * np.pi
    # 长轴长度
    a_samples = 1.0
    # 短轴长度
    b_samples = 2.0
    # 样本x 序列，并叠加正态分布的随机值
    x_samples = a_samples * np.cos(theta_samples) * np.cos(alpha_samples) \
                - b_samples * np.sin(theta_samples) * np.sin(alpha_samples) \
                + np.random.randn(100) * 0.05 * a_samples
    # 样本y 序列 ，并叠加正态分布的随机值
    y_samples = b_samples * np.sin(theta_samples) * np.cos(alpha_samples) \
                + a_samples * np.cos(theta_samples) * np.sin(alpha_samples) \
                + np.random.randn(100) * 0.05 * b_samples
    fit_ellipse(x_samples, y_samples)

ps:真不错，markerdown编辑器真不错