根据二叉树的中序和后续遍历
【摘要】 思路整体思路是这样的,后续遍历的最好一个结果是树的根节点,由后序遍历找到树的根节点。在把找到的根节点,在中序遍历中,根节点左边的是左子树,右边的是右子树。推导出左右子树的值。在把拆分都两个子树按照上述思路继续求解。 举个例子:例如:已知,中序遍历为45, 55, 57,59, 60, 67, 100, 101, 107后序遍历为45, 59, 57, 55, 67, 101, 107, 1...
思路
整体思路是这样的,后续遍历的最好一个结果是树的根节点,由后序遍历找到树的根节点。在把找到的根节点,在中序遍历中,根节点左边的是左子树,右边的是右子树。推导出左右子树的值。在把拆分都两个子树按照上述思路继续求解。
举个例子:
例如:已知,中序遍历为
45, 55, 57,59, 60, 67, 100, 101, 107
后序遍历为
45, 59, 57, 55, 67, 101, 107, 100, 60
求其前序遍历:
解:由于后序最后一个元素为60,则根结点为60,因此45,59,57,55为左子树的结点,67,101,107,100为右子树的结点。又由后序遍历的性质,可得55(45,59,57,55的最后一个),100(67,101,107,100的最后一个)为60的左右子树,依次类推,45,57为55的左右子树,67,107为100的左右子树。最后验证一下中序是否正确就可以画出前序遍历的结果了。60,55,100,45,57,107,59,101
代码实现
输入样例 :
ACBDFEG
ABDCGEF
输出样例 1:
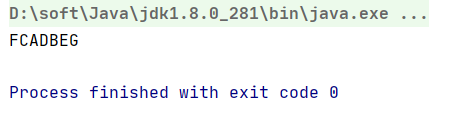
FCADBEG
代码如下:
public class Solution {
public static void main(String[] args) {
Solution s = new Solution();
String middle = "ACBDFEG";
String last = "ABDCGEF";
s.fun01(middle, last);
System.out.println(s.result);
}
String result = "";
void fun01(String middle, String last){
if (middle.length()==0||last.length()==0){
return;
}
if (middle.length()==1){
result = result+middle;
return;
}
String m = last.substring(last.length() - 1);
result = result + m;
//左右节点,中序
String[] split = new String[2];
split[0] = middle.substring(0,middle.indexOf(m));
split[1] = middle.substring(middle.indexOf(m)+1);
//后续
String[] str2 = new String[2];
str2[0] = last.substring(0,split[0].length());
str2[1] = last.substring(split[0].length(),last.length()-1);
for (int i = 0; i < 2; i++) {
fun01(split[i],str2[i]);
}
}
}
输出结果
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)