【路径规划】基于matlab遗传算法求解外卖订单动态变换模型【含Matlab源码 1983期】

一、VRP简介

1 VRP基本原理
车辆路径规划问题(Vehicle Routing Problem，VRP)是运筹学里重要的研究问题之一。VRP关注有一个供货商与K个销售点的路径规划的情况，可以简述为：对一系列发货点和收货点，组织调用一定的车辆，安排适当的行车路线，使车辆有序地通过它们，在满足指定的约束条件下（例如：货物的需求量与发货量，交发货时间，车辆容量限制，行驶里程限制，行驶时间限制等），力争实现一定的目标（如车辆空驶总里程最短，运输总费用最低，车辆按一定时间到达，使用的车辆数最小等）。
VRP的图例如下所示：

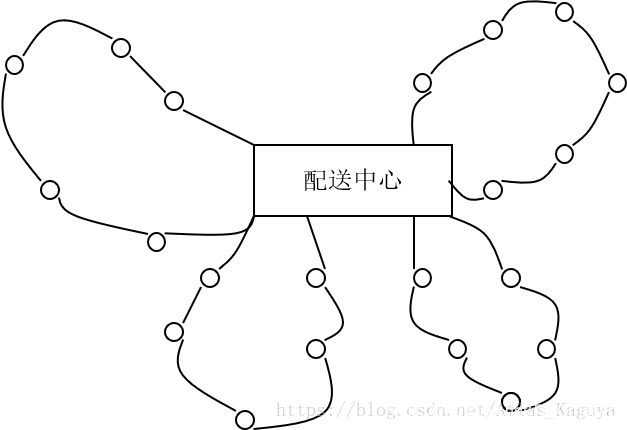
2 问题属性与常见问题
车辆路径问题的特性比较复杂，总的来说包含四个方面的属性：
（1）地址特性包括：车场数目、需求类型、作业要求。
（2）车辆特性包括：车辆数量、载重量约束、可运载品种约束、运行路线约束、工作时间约束。
（3）问题的其他特性。
（4）目标函数可能是总成本极小化，或者极小化最大作业成本，或者最大化准时作业。

3 常见问题有以下几类：
（1）旅行商问题
（2）带容量约束的车辆路线问题(CVRP)



该模型很难拓展到VRP的其他场景,并且不知道具体车辆的执行路径，因此对其模型继续改进。



（3）带时间窗的车辆路线问题
由于VRP问题的持续发展，考虑需求点对于车辆到达的时间有所要求之下，在车辆途程问题之中加入时窗的限制，便成为带时间窗车辆路径问题（VRP with Time Windows, VRPTW）。带时间窗车辆路径问题（VRPTW）是在VRP上加上了客户的被访问的时间窗约束。在VRPTW问题中，除了行驶成本之外, 成本函数还要包括由于早到某个客户而引起的等待时间和客户需要的服务时间。在VRPTW中，车辆除了要满足VRP问题的限制之外，还必须要满足需求点的时窗限制，而需求点的时窗限制可以分为两种，一种是硬时窗（Hard Time Window），硬时窗要求车辆必须要在时窗内到达，早到必须等待，而迟到则拒收；另一种是软时窗（Soft Time Window），不一定要在时窗内到达，但是在时窗之外到达必须要处罚，以处罚替代等待与拒收是软时窗与硬时窗最大的不同。


模型2(参考2017 A generalized formulation for vehicle routing problems)：
该模型为2维决策变量



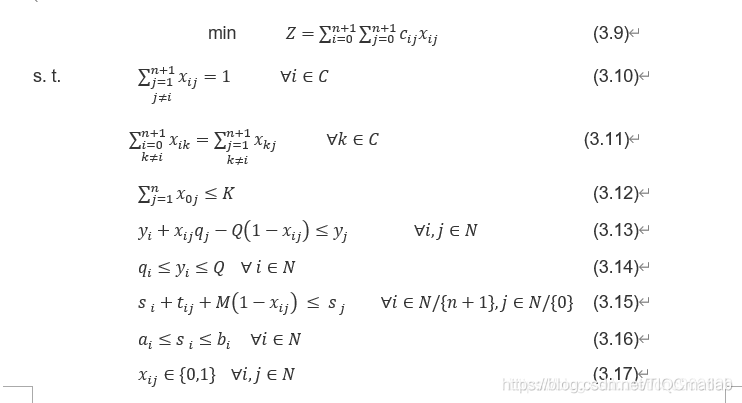
（4）收集和分发问题
（5）多车场车辆路线问题
参考(2005 lim，多车场车辆路径问题的遗传算法_邹彤, 1996 renaud)

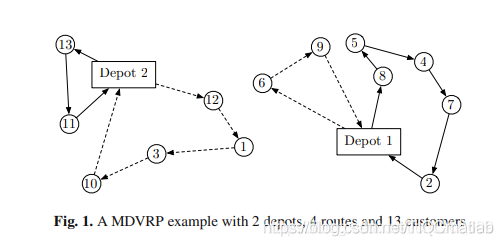
由于车辆是同质的，这里的建模在变量中没有加入车辆的维度。


（6）优先约束车辆路线问题
（7）相容性约束车辆路线问题
（8）随机需求车辆路线问题

4 解决方案
（1）数学解析法
（2）人机交互法
（3）先分组再排路线法
（4）先排路线再分组法
（5）节省或插入法
（6）改善或交换法
（7）数学规划近似法
（8）启发式算法

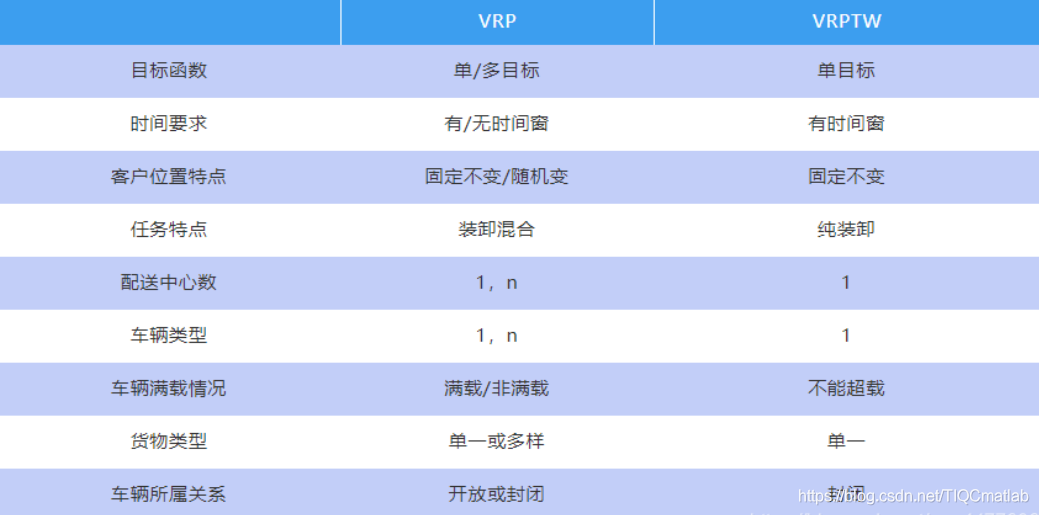
5 VRP与VRPTW对比

二、部分源代码

clear
clc
close all
tic
%% 读取数据
load('shuju7');
bl=0;
%% 提取数据信息
E=shuju(1,4);                                                    %初始点时间窗开始时间
L=shuju(1,5);                                                    %初始点心时间窗结束时间
zuobiao=shuju(1:end-2,2:3);                                       %所有点的坐标x和y
zb=shuju(1:end,2:3);
dtzb=shuju(end-1:end,2:3);
zuobiao=[zuobiao(:,1),-zuobiao(:,2)];
zb=[zb(:,1),-zb(:,2)];
customer=zuobiao(2:end,:);                                       %顾客坐标
dtcustomer=zuobiao(end-1:end,:);
cusnum=size(customer,1);                                         %顾客数
v_num=1;                                                        %车辆数
a=shuju(2:end,4);                                                %顾客时间窗开始时间[a[i],b[i]]
b=shuju(2:end,5);                                                %顾客时间窗结束时间[a[i],b[i]]
F=shuju(2:end,1);

% dist=Distanse(zb); %根据坐标的欧式距离矩阵

dist=load('shiji7.mat');%D导入距离矩阵
dist=struct2cell(dist);
dist=cell2mat(dist);
%% 遗传算法参数设置

chesu=300;%车速
alpha=100000;                                                       %违反的容量约束的惩罚函数系数
belta=chesu/1000;%违反时间窗约束的惩罚函数系数
belta2=1;

NIND=100;                                                       %种群大小
MAXGEN=100;                                                     %迭代次数
Pc=0.9;                                                         %交叉概率
Pm=0.05;                                                        %变异概率
GGAP=0.9;                                                       %代沟(Generation gap)
N=cusnum;
%% 初始化种群
FF=F(1:end-2,:);
[s,g,sj,gk,Chrom]=init(cusnum,NIND,FF);                             %构造初始解

%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')

[VC,TD,violate_cus]=decode(Chrom(1,:),cusnum,a,b,L,dist,chesu,bl);
% disp(['总距离：',num2str(TD)]);
disp(['车辆行驶总距离：',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
gen=1;
subplot(2,2,1);
hold on;box on
xlim([0,MAXGEN])
title('优化过程')
xlabel('代数')
ylabel('最优值')
[ObjV,bsv,gs,w1,w2]=calObj(Chrom,cusnum,a,b,L,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
preObjV=min(ObjV);
%%
while gen<=MAXGEN
    %% 计算适应度
    [ObjV,bsv,gs,w1,w2]=calObj(Chrom,cusnum,a,b,L,dist,alpha,belta,belta2,chesu,bl);           %计算种群目标函数值
    line([gen-1,gen],[preObjV,min(ObjV)]);pause(0.0001)%画图 最优函数
    preObjV=min(ObjV);
    FitnV=Fitness(ObjV);
    %% 选择 
     SelCh=Select(Chrom,FitnV,GGAP);
    %% OX交叉操作
    SelCh=Recombin(SelCh,Pc,s,g,sj,gk);
    %% 变异
    SelCh=Mutate(SelCh,Pm,s,g,sj,gk);
    %% 重插入子代的新种群
    Chrom=Reins(Chrom,SelCh,ObjV);
    %% 打印当前最优解
    [ObjV,bsv,gs,w1,w2]=calObj(Chrom,cusnum,a,b,L,dist,alpha,belta,belta2,chesu,bl);           %计算种群目标函数值
    [minObjV,minInd]=min(ObjV);
    disp(['第',num2str(gen),'代最优解:'])    
    [bestVC,bestTD,best_viocus]=decode(Chrom(minInd(1),:),cusnum,a,b,L,dist,chesu,bl);
    disp(['车辆行驶总距离：',num2str(bestTD)]);
    fprintf('\n')
    %% 更新迭代次数
    gen=gen+1 ;
end


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/125812012