单源最短路径
目录
一,单源最短路径 Dijskra
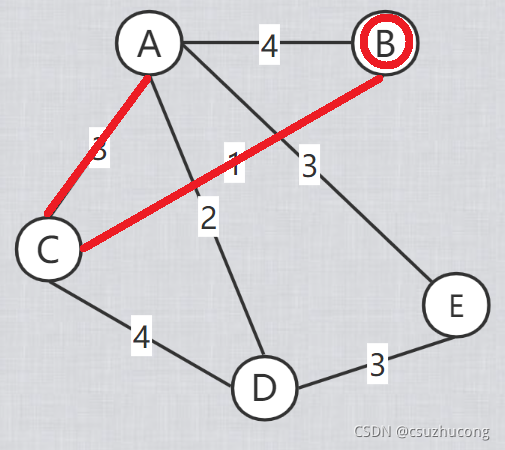
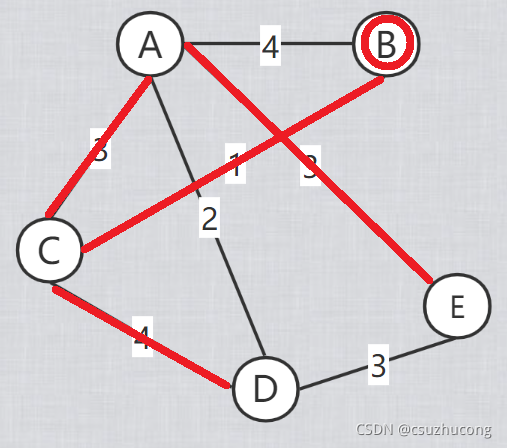
把点分为已经确定最短路的点和还没确定的点,每次新增一个确定最短路的点,确定之后根据它来对剩下的点刷新从起点到该点的可能的最短路,
每次都在剩下的点中,选取离起点最近的点加入到确定最短路的集合中,直到所有的点都确定最短路。



二,无向图实战
HDU 1874 畅通工程续
题目:
Description
某省自从实行了很多年的畅通工程计划后,终于修建了很多路。不过路多了也不好,每次要从一个城镇到另一个城镇时,都有许多种道路方案可以选择,而某些方案要比另一些方案行走的距离要短很多。这让行人很困扰。
现在,已知起点和终点,请你计算出要从起点到终点,最短需要行走多少距离。
Input
本题目包含多组数据,请处理到文件结束。
每组数据第一行包含两个正整数N和M(0<N<200,0<M<1000),分别代表现有城镇的数目和已修建的道路的数目。城镇分别以0~N-1编号。
接下来是M行道路信息。每一行有三个整数A,B,X(0<=A,B<N,A!=B,0<X<10000),表示城镇A和城镇B之间有一条长度为X的双向道路。
再接下一行有两个整数S,T(0<=S,T<N),分别代表起点和终点。
Output
对于每组数据,请在一行里输出最短需要行走的距离。如果不存在从S到T的路线,就输出-1.
Sample Input
3 3
0 1 1
0 2 3
1 2 1
0 2
3 1
0 1 1
1 2
Sample Output
2
-1
太懒了,懒得用邻接表+优先队列了,直接用邻接矩阵然后暴力的求解。
用len记录任何2个点之间的距离,minlen记录一个点到s的最短距离。
minlen是不断更新的,只有访问过之后,即visit变成1之后,minlen才是真的到s的最短距离,在这之前都只是它的上界。
代码:
-
#include<iostream>
-
#include<string.h>
-
using namespace std;
-
-
int n, m, s, t;
-
int con = 2000000;
-
int len[200][200];
-
int minlen[200];
-
int visit[200];
-
-
void dijkstra(int k)
-
{
-
if (minlen[k] >= con)return;
-
visit[k] = 1;
-
for (int i = 0; i < n; i++)
-
{
-
if (minlen[i]>minlen[k] + len[i][k])minlen[i] = minlen[k] + len[i][k];
-
}
-
int l = con, key = -1;
-
for (int i = 0; i < n; i++)
-
{
-
if (visit[i] == 0 && l>minlen[i])
-
{
-
key = i;
-
l = minlen[i];
-
}
-
}
-
if (key < 0)return;
-
dijkstra(key);
-
}
-
-
int main()
-
{
-
int a, b, x;
-
while (scanf("%d%d", &n, &m) != -1)
-
{
-
for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)len[i][j] = con;
-
while (m--)
-
{
-
scanf("%d%d%d", &a, &b, &x);
-
if (len[b][a]>x)len[a][b] = len[b][a] = x;
-
}
-
scanf("%d%d", &s, &t);
-
for (int i = 0; i < n; i++)minlen[i] = len[i][s];
-
memset(visit, 0, sizeof(visit));
-
minlen[s] = 0;
-
dijkstra(s);
-
if (minlen[t]<con)printf("%d\n", minlen[t]);
-
else printf("-1\n");
-
}
-
return 0;
-
}
不过还是挺快的,15ms AC
这个题目有一个略坑的地方,2个城市之间不一定只有1条路,所以更新len的时候需要判断。
con是用200*10000得到的,con的作用是保证如果一个点和s是连通的,那么它们之间的距离一定小于con。
所以这个con也就是相当于无穷大的实现。
三,有向图实战
力扣 743. 网络延迟时间
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:
输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1
输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2
输出:-1
提示:
1 <= k <= n <= 100
1 <= times.length <= 6000
times[i].length == 3
1 <= ui, vi <= n
ui != vi
0 <= wi <= 100
所有 (ui, vi) 对都 互不相同(即,不含重复边)
-
//输入边集{{1,2}{1,3}{2,3}},输出邻接表{1:{2,3},2:{3}}
-
map<int, vector<int>> edgeToAdjaList(vector<vector<int>>& v)
-
{
-
map<int,vector<int>> ans;
-
for (auto &vi : v) {
-
ans[vi[0]].push_back(vi[1]);
-
}
-
return ans;
-
}
-
//输入带权边集,输出边和权的映射
-
map<pair<int, int>, int> edgeToValueMap(vector<vector<int>>& v)
-
{
-
map<pair<int, int>, int>m;
-
for (auto& vi : v) {
-
m[{vi[0], vi[1]}] = vi[2];
-
}
-
return m;
-
}
-
-
struct Node
-
{
-
int id;
-
int len;
-
};
-
class cmp
-
{
-
public:
-
bool operator()(Node a, Node b)
-
{
-
return a.len > b.len;
-
}
-
};
-
-
class Solution {
-
public:
-
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
-
map<int, int>m;
-
for (int i = 1; i <= n; i++)m[i] = INT_MAX;
-
map<int, vector<int>> adja = edgeToAdjaList(times);
-
map<pair<int, int>, int> value = edgeToValueMap(times);
-
priority_queue< Node, vector< Node>, cmp>que;
-
map<int, int>visit;
-
que.push({ k,0 });
-
m[k] = 0;
-
while (!que.empty())
-
{
-
Node nod = que.top();
-
que.pop();
-
if (visit[nod.id])continue;
-
visit[nod.id] = 1;
-
for (auto& vi : adja[nod.id]) {
-
if (nod.len + value[{nod.id, vi}] < m[vi]) {
-
que.push({ vi, m[vi] = nod.len + value[{nod.id, vi}] });
-
}
-
}
-
}
-
int ans = 0;
-
for (int i = 1; i <= n; i++) {
-
if (m[i] == INT_MAX)return -1;
-
ans = max(ans, m[i]);
-
}
-
return ans;
-
}
-
};
文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/125795143
- 点赞
- 收藏
- 关注作者



评论(0)