当当+搜狐+好未来笔试题+知识点总结

一、情景回顾

• 时间:2016.9.21 15：00-21：00
• 地点:山东省网络环境智能计算技术重点实验室
• 事件:当当笔试、搜狐笔试、好未来笔试

3场笔试中好未来相对简单点。

二、好未来编程题

2.1 马踏棋盘(贪心算法)

马踏棋盘是经典的程序设计问题之一，主要的解决方案有两种：一种是基于深度优先搜索的方法，另一种是基于贪婪算法的方法。第一种基于深度优先搜索(DFS)的方法是比较常用的算法，深度优先搜索算法也是数据结构中的经典算法之一，主要是采用递归的思想，一级一级的寻找，最后找到合适的解。而基于贪婪的算法则是依据贪婪算法的思想设置一种标准，然后依据标准进行选择，从而得到解，但是他不一定能够得到最优解。

关于马踏棋盘的基本过程：国际象棋的棋盘为8*8的方格棋盘。现将"马"放在任意指定的方格中，按照"马"走棋的规则将"马"进行移动。要求每个方格只能进入一次，最终使得"马"走遍棋盘的64个方格。

深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次.（来自百度）基于深度优先搜索的算法就是依据当前点找到下一个可能的点，然后对这个点进行深度优先搜索，然后依次递归，当出现条件不满足时，退回来，采用其他的路径进行搜索，最后肯定能够得到对应的结果。

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。

本题与经典的马踏棋盘问题的区别就是点可以重复走。给定两点，判断是否走得通，并记录某次走通的路径。

package cn.edu.ujn.practice;

/**
 * 贪心算法解决马踏棋盘问题
 * 棋盘有64个位置，“日”字走法，刚好走满整个棋盘
 * @author SHQ
 * @date 2016-09-22
 */
public class HorseStep {
	static final int[] dx = { -1, -2, -2, -1, 1, 2, 2, 1 }; // x方向的增量
	static final int[] dy = { 2, 1, -1, -2, -2, -1, 1, 2 }; // y方向的增量
	static final int N = 8;
	static int[][] board = new int[N][N]; // 棋盘

	// 计算结点出口
	int waysOut(int x, int y) {
		int tx, ty;
		int count = 0;
		// 结点位置非法或已踏过，返回-1
		if (x < 0 || y < 0 || x >= N || y >= N || board[x][y] > 0) {
			return -1;
		}
		for (int i = 0; i < N; ++i) {
			tx = x + dx[i];
			ty = y + dy[i];
			if (tx < 0 || ty < 0 || tx >= N || ty >= N) {
				continue;
			}
			// 如果棋子的下个出路可行，则出路数自加一次
			if (board[tx][ty] == 0) {
				count++;
			}
		}
		return count;
	}

	// 按结点出口数，从小到大排序
	void sortnode(HorseNode[] hn, int n)// 采用简单排序法，因为子结点数最多只有8
	{
		int i, j, t;
		HorseNode temp;
		for (i = 0; i < n; ++i) {
			for (t = i, j = i + 1; j < n; ++j)
				if (hn[j].waysOutNum < hn[t].waysOutNum)
					t = j;
			if (t > i) {
				temp = hn[i];
				hn[i] = hn[t];
				hn[t] = temp;
			}
		}
	}

	// 搜索函数,count代表当前第几步
	void dfs(int x, int y, int count) {
		int i, tx, ty;
		HorseNode[] tExit = new HorseNode[N]; // 记录出口结点的出口数

		if (count > N * N) {
			output();
			return;
		}
		// 计算[x,y]的出口结点和出口结点的出口数
		for (i = 0; i < N; i++) {
			tx = x + dx[i];
			ty = y + dy[i];
			HorseNode h = new HorseNode();
			tExit[i] = h;
			tExit[i].x = tx;
			tExit[i].y = ty;
			tExit[i].waysOutNum = waysOut(tx, ty);
		}
		
		sortnode(tExit, N);
		
		for(i = 0; tExit[i].waysOutNum < 0; ++i)
			;
		for(; i < N; ++i){
			tx = tExit[i].x;
			ty = tExit[i].y;
			board[tx][ty] = count;
			dfs(tx, ty, count + 1);
			/*如果上面dfs()往下一步走不通，则回溯到这里重置chessboard[tx][ty]为0，接着i++,又循环...... */
			board[tx][ty] = 0;
		}
	}
	
	public static void main(String[] args) {
		int x = 1;
		int y = 3;
		HorseStep test = new HorseStep();
		board[x][y] = 1;
		test.dfs(x, y, 2);
	}

	//打印结果
	void output(){
		for(int i = N - 1; i >= 0; --i){
			for(int j = 0; j < N; ++j){
				System.out.printf("%2d ", board[i][j]);
			}
			System.out.println();
		}
		System.exit(0);
	}
	
}

// 下一个走法的方向类
class HorseNode {
	int x;
	int y;
	int waysOutNum;
}

2.2 TSP(旅行商问题)

package cn.edu.ujn.practice;

import java.util.ArrayList;
import java.util.List;
import java.util.Map;
import java.util.HashMap;

/**
 * 动态规划求解TSP问题
 * @author SHQ
 *
*/
public class TSP {

	private double[][] dArray; 	// 距离矩阵
	private int length; 		// 距离矩阵的长度
	private int lengthOfLength; // 距离矩阵长度字符串的长度
	private String allzero = "";// 0组成的字符串最大值是length个(length - 1)连接起来的字符串，同样最小值是length个0连接起来
	private String biggest = "";
	private List<String> list = new ArrayList<String>(); // 城市流列表
	private Map<String, Double> store;		// 存储中间数据
	private String notExist = "不存在";
	private String firnalRoad = notExist; 	// 最终的路径，即距离矩阵的列号取值
	private String firnalCityFlow = ""; 	// 最终形成的城市流
	private String min = notExist; 			// 最终求得的最小值
	private String allFlowTime = notExist; 	// 求解所有城市流的时间
	private String guihuaTime = notExist; 	// 动态规划的时间

	/** Creates a new instance of TwentyTwo */
	public TSP(double[][] dArray) {
		if (this.check(dArray)) {
			this.dArray = dArray;
			this.length = dArray.length;
			this.lengthOfLength = (length - 1 + "").length();
			for (int zeroLength = 0; zeroLength < (length * lengthOfLength);) {
				allzero += 0;
				zeroLength = allzero.length();
			}
			for (int i = this.length; i > 0; i--) {
				this.biggest += this.toLengthOfLength(i - 1);
			}
			long start = System.currentTimeMillis();
			this.allFlow();
			long end = System.currentTimeMillis();
			this.allFlowTime = end - start + "毫秒";
			start = System.currentTimeMillis();
			this.initstoreMap();
			this.guihua(this.length - 2);
			end = System.currentTimeMillis();
			this.guihuaTime = end - start + "毫秒";
		}
	}

	public String getFirnalRoad() {
		return this.firnalRoad;
	}

	public String getFirnalCityFlow() {
		if ("".equals(this.firnalCityFlow)) {
			return this.notExist;
		}
		return this.firnalCityFlow;
	}

	public String getMin() {
		return this.min;
	}

	public String getAllFlowTime() {
		return this.allFlowTime;
	}

	public String getGuihuaTime() {
		return this.guihuaTime;
	}

	// 输入距离矩阵的有效性判读
	private boolean check(double[][] dArray) {
		if (dArray.length < 3) {
			System.out.println("错误信息：距离矩阵长度过小");
			return false;
		}
		for (int i = 0; i < dArray.length; i++) { // 每个double[]的长度都进行判断
			if (dArray.length != dArray[i].length) {
				// 非方阵
				System.out.println("错误信息：距离数组长度不合法");
				return false;
			}
		}
		for (int i = 0; i < dArray.length; i++) {
			if (!oneZero(dArray[i], i)) {
				System.out.println("错误信息：距离数组顺序或元素值设置不合法");
				return false;
			}
		}
		return true;
	}

	// 对于一个doulbe类型的数组，只有第i个元素为0的判断

	private boolean oneZero(double[] dArray, int i) {
		int numOfZero = 0;
		for (double d : dArray) {
			if (d == 0.0) {
				numOfZero++;
			}
		}
		if (numOfZero == 1 && (dArray[i] == 0)) {
			return true;
		} else {
			return false;
		}
	}

	// 判断一个城市流是否合法

	private boolean oneFlow(String str) {
		// 将一个字符串更改为一个字符链表
		List<String> listString = new ArrayList<String>();
		for (int i = 0; i < (this.length * this.lengthOfLength);) {
			listString.add(str.substring(i, i + this.lengthOfLength));
			i += this.lengthOfLength;
		}
		// 如果有相同的元素，则false
		for (int i = 0; i < (this.length - 1); i++) {
			for (int j = i + 1; j < this.length; j++) {
				if (listString.get(i * this.lengthOfLength).equals(
						listString.get(j * this.lengthOfLength))) {
					return false;
				}
			}
		}
		// 如果有距离矩阵全0对角线上的元素，则false
		for (int i = 0; i < listString.size(); i++) {
			if (Integer.parseInt(listString.get(i)) == i) {
				return false;
			}
		}
		// 排除没有遍历所有城市的情况（从0点出发到达0点）
		Map<Integer, Integer> map = new HashMap<Integer, Integer>();
		for (int i = 0; i < this.length;) {
			map.put(i,
					Integer.parseInt(str.substring(i, i + this.lengthOfLength)));
			i += this.lengthOfLength;
		}
		int allcity = 0;
		for (int i = 0;;) {
			i = map.get(i);
			allcity++;
			if (i == 0) {
				break;
			}
		}
		if (allcity < this.length) {
			return false;
		}
		return true;
	}

	// 初始化存储map

	private void initstoreMap() {
		this.store = new HashMap<String, Double>();
		// 存距离矩阵最后一行可能的列号
		for (int i = 0; i < this.length - 1; i++) {
			this.store.put(this.toLengthOfLength(i),
					this.dArray[this.length - 1][i]);
		}
		// 存距离矩阵倒数两行可能的列号
		for (int i = 0; i < this.length; i++) {
			if (i == this.length - 2)
				continue;
			for (int j = 0; j < this.length - 1; j++) {
				if (i == j) {
					continue;
				}
				store.put(
						this.toLengthOfLength(i) + this.toLengthOfLength(j),
						this.dArray[this.length - 2][i]
								+ store.get(this.toLengthOfLength(j)));
			}
		}
	}

	// 两个相近的城市流，前length - 2 - temp个数相同，后面不同，用动态规划实现
	private void guihua(int temp) {
		if (list.size() == 1) {
			this.firnalRoad = list.get(0);
			this.thePrint(list.get(0));
			this.min = this.store.get(list.get(0)) + "";
			return;
		}
		for (int i = 0; i < (list.size() - 1); i++) {
			int next = (i + 1);
			if (list.get(i)
					.substring(0, temp * this.lengthOfLength)
					.equals(list.get(next).substring(0,
							temp * this.lengthOfLength))) {
				double iValue = 0;
				double nextValue = 0;

				iValue = this.dArray[temp][Integer.parseInt(list.get(i)
						.substring(temp, temp + this.lengthOfLength))]
						+ store.get(list.get(i).substring(
								(temp + 1) * this.lengthOfLength));
				nextValue = this.dArray[temp][Integer.parseInt(list.get(next)
						.substring(temp, temp + this.lengthOfLength))]
						+ store.get(list.get(next).substring(
								(temp + 1) * this.lengthOfLength));

				this.store.put(list.get(i)
						.substring(temp * this.lengthOfLength), iValue);
				this.store.put(
						list.get(next).substring(temp * this.lengthOfLength),
						nextValue);

				if (iValue >= nextValue) {
					list.remove(i);
				} else {
					list.remove(next);
				}
				i--;
			}
		}
		this.guihua(temp - 1);
	}

	// 组成所有的城市流
	private void allFlow() {
		while (!this.biggest.equals(this.allzero)) {
			this.allzero = this.addone(this.allzero);
			if (this.oneFlow(this.allzero)) {
				this.list.add(this.allzero);
			}
		}
	}

	// 将length进制的字符串加1操作

	private String addone(String str) {
		List<String> listString = new ArrayList<String>();
		for (int i = 0; i < (this.length * this.lengthOfLength);) {
			listString.add(str.substring(i, i + this.lengthOfLength));
			i += this.lengthOfLength;
		}
		for (int i = (length - 1); i > -1; i--) {
			int last = Integer.parseInt(listString.get(i));
			if (last == (length - 1)) {
				last = 0;
				String strLast = this.toLengthOfLength(last);
				listString.set(i, strLast);
			} else {
				last++;
				String strLast = this.toLengthOfLength(last);
				listString.set(i, strLast);
				break;
			}
		}
		String ret = "";
		for (String s : listString) {
			ret += s;
		}
		return ret;
	}

	// 如果一个int字符串长度不够lengthOfLength 则补足

	private String toLengthOfLength(Object i) {
		String returnString = i.toString();
		while (returnString.length() < this.lengthOfLength) {
			returnString = (0 + returnString);
		}
		return returnString;
	}

	// 将一个字符串键值映射，并标准输出

	private void thePrint(String str) {
		Map<Integer, Integer> map = new HashMap<Integer, Integer>();
		for (int i = 0; i < this.length;) {
			map.put(i, Integer.parseInt(str.substring(i, i + this.lengthOfLength)));
			i += this.lengthOfLength;
		}
		String cityFlow = this.toLengthOfLength(0);
		for (int i = 0;;) {
			i = map.get(i);
			cityFlow += this.toLengthOfLength(i);
			if (i == 0) {
				break;
			}
		}
		for (int i = 0; i < this.length + 1;) {
			if (i < (this.length)) {
				this.firnalCityFlow += Integer.parseInt(cityFlow.substring(i, i	+ this.lengthOfLength)) + "->";
			} else {
				this.firnalCityFlow += Integer.parseInt(cityFlow.substring(i, i	+ this.lengthOfLength));
			}
			i += this.lengthOfLength;
		}
	}

	public static void main(String[] args) {
		double[][] first = {		 // 各个节点之间路径长度的二维数组
		{ 0, 2, 1, 3, 4, 5, 5, 6 },
		{ 1, 0, 4, 4, 2, 5, 5, 6 },
		{ 5, 4, 0, 2, 2, 6, 5, 6 },
		{ 5, 2, 2, 0, 3, 2, 5, 6 },
		{ 4, 2, 4, 2, 0, 3, 5, 6 },
		{ 4, 2, 4, 2, 3, 0, 5, 6 },
		{ 4, 2, 4, 2, 4, 3, 0, 6 },
		{ 4, 2, 4, 2, 8, 3, 5, 0 } };
		long start = System.currentTimeMillis();
		TSP ff = new TSP(first);
		System.out.println("路径是：" + ff.getFirnalRoad());
		System.out.println("城市顺序：" + ff.getFirnalCityFlow());
		System.out.println("最小值：" + ff.getMin());
		System.out.println("生成所有合法城市流用时：" + ff.getAllFlowTime());
		System.out.println("动态规划求解过程用时：" + ff.getGuihuaTime());
		long end = System.currentTimeMillis();
		System.out.println("总用时：" + (end - start));
	}
}

三、当当编程题

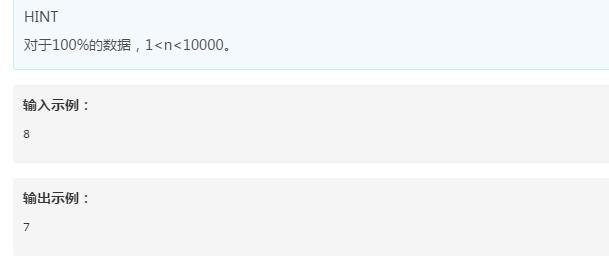
四、搜狐编程题

4.1 袋鼠过河

4.2 保留最大的数

4.3 彩色宝石项链

时间限制：C/C++语言 1000MS；其他语言 3000MS
内存限制：C/C++语言 65536KB；其他语言 589824KB
题目描述：

有一条彩色宝石项链，是由很多种不同的宝石组成的，包括红宝石，蓝宝石，钻石，翡翠，珍珠等。有一天国王把项链赏赐给了一个学者，并跟他说，你可以带走这条项链，但是王后很喜欢红宝石，蓝宝石，紫水晶，翡翠和钻石这五种，我要你从项链中截取连续的一小段还给我，这一段中必须包含所有的这五种宝石，剩下的部分你可以带走。如果无法找到则一个也无法带走。请帮助学者找出如何切分项链才能够拿到最多的宝石。

输入

我们用每种字符代表一种宝石，A表示红宝石，B表示蓝宝石，C代表紫水晶，D代表翡翠，E代表钻石，F代表玉石，G代表玻璃等等，我们用一个全部为大写字母的字符序列表示项链的宝石序列，注意项链是首尾相接的。每行代表一种情况。

输出

输出学者能够拿到的最多的宝石数量。每行一个。

样例输入
ABCYDYE
ATTMBQECPD
样例输出
1
3
必须掌握的知识点
通过参加若干次笔试，发现重复考的知识点主要有排序算法(快排)、设计模式(单例、观察者)、类迷宫问题(递归+回溯)、贪心算法、DFS&BFS。

五、拓展阅读

-《剑指Offer专刊》