【聚类算法】基于matlab划分法k-means聚类算法【含Matlab源码 1941期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【聚类算法】基于matlab划分法k-means聚类算法【含Matlab源码 1941期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、基于划分的K-means聚类算法简介

随着信息技术的快速发展及广泛推进,数据挖掘成为当今社会研究的一个热点领域,聚类分析是数据挖掘中的一项核心技术,它通过研究数据的分布特征来发现数据背后隐藏的事物内部规律。聚类算法有很多种,每一种算法都有自己的独特之处。K-means算法是聚类分析的经典算法之一,文中主要对K-means算法进行阐述。

1 聚类分析概述
聚类分析是人的一项重要活动,比如,小孩子通过不断学习都能够区分动物和植物,也能够区分鸡和狗。聚类与分类不同,分类是按照一定的标准把数据分成不同的类别,聚类是通过观察数据的特征寻找这个标准。

聚类分析的核心是聚类,即将物理或抽象对象的集合分成相似的对象类的过程。通过聚类把数据分成不同的集合,同一个集合中的数据对象彼此相似,不同数据集合的对象之间彼此相异。形成聚类的原则是使类内部的相似性最大,类间的相似性最小。聚类的研究方法有很多,用的比较多的是K-means(K-平均值)、BIRCH算法、clara算法、eLIQuE算法、chameleon(变色龙)算法等。

聚类可以对迅猛增长的数据加以组织,人们通过聚类可以发现一些数据分布的特征,因此成为比较活跃的研究课题。目前,很多领域已经成功地应用了该项技术,包括市场研究、人工智能和图像处理、生物学、数据压缩等领域[2]。例如,在生物学领域,聚类可以自动对物种分类,依据是物种特征;还可以更好地理解生物学中基因的功能。在商业中,市场分析员通过聚类分析可以很容易发现顾客库中不同的顾客群。聚类还可以应用于客户关系管理,对从接触点收集到的数据进行分析,可以得出有价值的知识,以便用于改进营销方案、制定定价和促销策略。

2 K-means算法
2.1 K-means算法基本思想
K-means算法,也被称为K-均值,是最常用、最著名的一种聚类算法。K-means算法是把n个对象分成K个簇,用簇中对象的均值表示每个簇的质心,通过迭代使每个簇内的对象不再发生变化为止。这时准则函数达到最优,每个簇内相似度高,簇间相似度低。其过程描述如下:

(1)首先,随机地选择K个对象,代表要分成的K个簇的初始均值或中心。
(2)计算其余对象与各个均值的距离,然后把它们分别划分到距离中心最近的簇中。
(3)计算每个簇中所有对象的平均值,作为每个新的簇中心
(4)计算所有对象与新的K个中心的距离,根据“距离中心最近”原则,重新划分所有对象到各个簇中
(5)重复(3)、(4),直至所有簇中心不变为止。

2.2 K-means算法划分聚类的三个关键点
(1)数据对象的划分
(1)距离度量的选择
K-means算法比较适合处理连续型属性,对离散型属性不适合。在计算数据对象之间的距离时要选择合适的相似性度量。比较著名的距离度量是欧几里得距离和曼哈顿距离[3],其中最常用的是欧几里得距离,其公式如下:

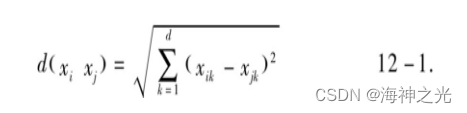
这里xi,xj表示两个d维数据对象,xi=(xi1,xi2,…,xid),xj=(xj1,xj2,…,xjd),d(xi,xj)表示对象xi和xj之间的距离,距离越小,二者越相似;距离越大,二者差异就越大。

根据欧几里得距离,计算出每一个数据对象与各个簇中心的距离。

(2)选择最小距离,即如果

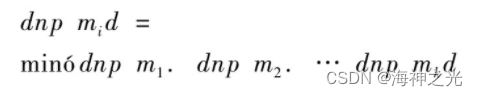
那么,p∈ci;P表示给定的数据对象;m1,m2,…,mk分别表示簇c1,c2,…,ck的初始均值或中心;

(2)准则函数的选择。K-means算法采用平方误差准则函数来评价聚类性能,其公式如下:

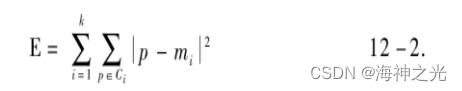
E表示数据库中所有对象的平方误差和,P表示给定的数据对象,mi表示簇ci的均值。

(3)簇中心的计算。用每一簇的平均值作为计算相似度簇中心的依据,其公式如下:

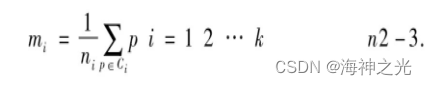
这里假设簇c1,c2,…,ck中的数据对象个数分别为n1,n2,…,nk。

2.3 K-means算法的实现
(1)划分数据对象。选择k个数据对象作为初始k个聚类的中心,根据欧几里得距离公式,依次比较每个数据对象与各个中心的距离,选择距离中心最近的簇,依次把n个对象划分到k个簇中[4]。完成第一次划分之后,重新计算新的簇的中心,然后开始重新划分数据对象,直到新的簇中心不再发生变化,停止迭代。

(2)计算簇中心。每次划分数据对象之后,都要重新计算簇中心,直到簇中心不再发生变化为止。

三、部分源代码

 clear all;
close all;
clc;
%第一类数据
mu1=[10 3 3];  %均值
S1=[0.3 0 0;0 0.35 0;0 0 0.3];  %协方差
data1=mvnrnd(mu1,S1,100);   %产生高斯分布数据
%%第二类数据
mu2=[5 10 5];
S2=[0.3 0 0;0 0.35 0;0 0 0.3];
data2=mvnrnd(mu2,S2,150);
mu3=[10 10 10];
S3=[0.3 0 0;0 0.35 0;0 0 0.3];
data3=mvnrnd(mu3,S3,200);
%第三个类数据
mu4=[15 15 15];
S4=[0.3 0 0;0 0.35 0;0 0 0.3];
data4=mvnrnd(mu4,S4,50);
data=[data1;data2;data3;data4];   %这里的data是不带标号的
plot3(data(:,1),data(:,2),data(:,3),'+')
grid on;
hold on;
k=7;
r=10;
p=2;
for i=k:-1:2 
   if p == 0
      break;
   end
   k=i
    [resX resY resZ seedX seedY seedZ record] = FunK_mean3D(data(:,1),data(:,2),data(:,3),k,r);
  % 下面是标记出每一个类别的类别代表点 
  for j=k:-1:2
      p=0;
      j
      for m=j-1:-1:1
          m
          power(seedX(m)-seedX(j),2)+power(seedY(m)-seedY(j),2)+power(seedZ(m)-seedZ(j),2)
         if (power(seedX(m)-seedX(j),2)+power(seedY(m)-seedY(j),2)+power(seedZ(m)-seedZ(j),2))<r
            p=1
            break;
         end
      end
      p
       if p==1
          break;
       end
  end
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
 

四、运行结果

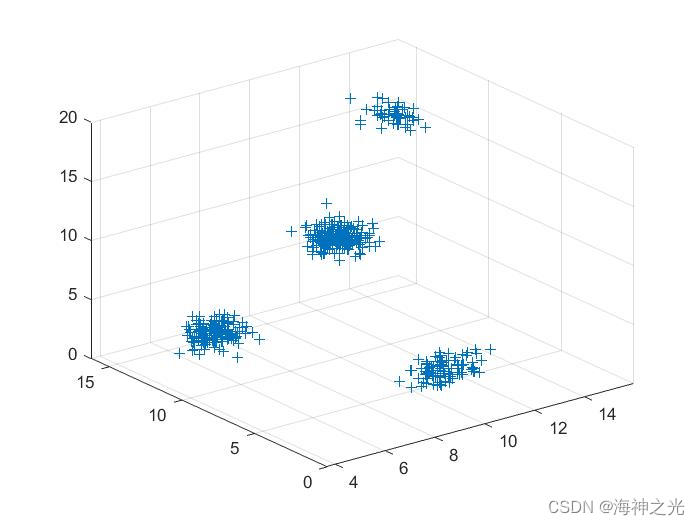
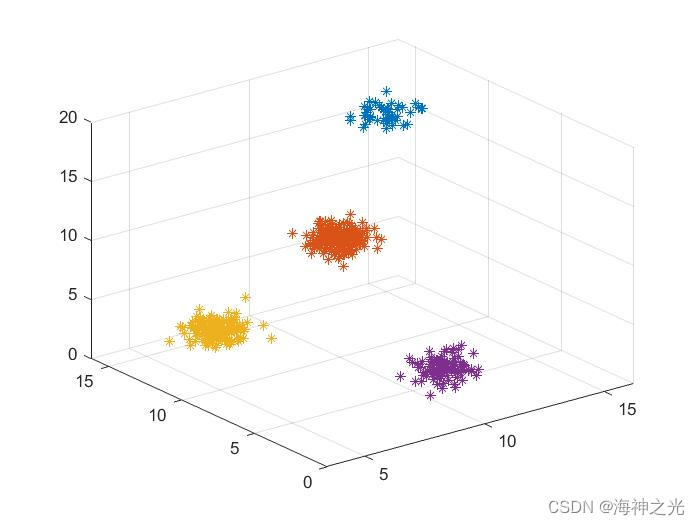
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]丁丽,孙高峰.基于划分的K-means聚类算法[J].宜春学院学报. 2013,35(06)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/125696414