【光学】基于matlab泊松亮斑仿真【含Matlab源码 1937期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【光学】基于matlab泊松亮斑仿真【含Matlab源码 1937期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、泊松亮斑的模拟仿真研究

1 衍射光强分布的模拟仿真
圆盘衍射的示意图显示在图1中。光强为I0的入射光平行于Z轴方向入射到衍射平面上,衍射平面位于z0处。对于衍射平面上任意一点(x0,y0,z0),若处于圆盘遮挡的位置,光强度U(x0,y0,z0)=0,反之光强度则为入射光强度。观察平面位于z处,观察平面上任意一点(x,y,z)的复振幅分布可以通过菲涅尔衍射的基本公式获得:

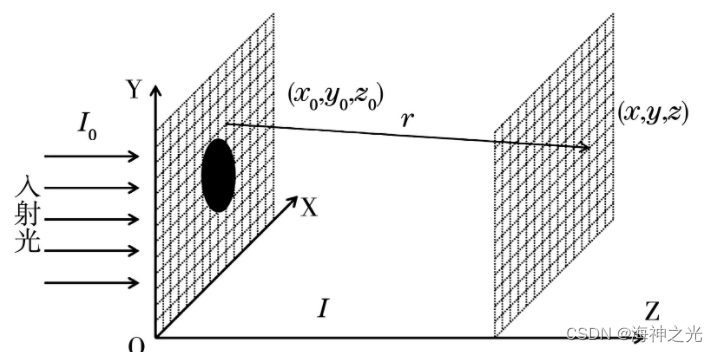
图1 圆盘衍射的示意图

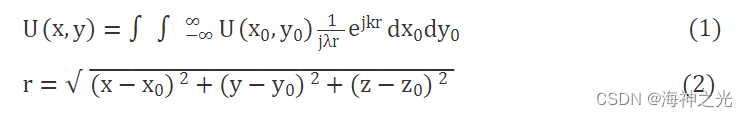
其中,λ为入射光的波长,k为倾斜因子,z-z0为观察平面到衍射平面之间的距离l。根据菲涅尔衍射的定义,观察平面上任意一点的复振幅是衍射平面上所有点的复振幅到该点的积分。因此,在仿真模拟中,我们将衍射平面和观察平面分别划分为很小的微元网格,观察平面上任意一个微元的复振幅是衍射平面上所有微元的复振幅到该点的振幅总和。该方法虽然计算量相对较大,但是通过设置衍射屏的透光数据,可以计算不规则衍射屏的衍射。

2 入射光波长对泊松亮斑的影响
为了让模拟仿真更具有代表性意义,我们选取了200 nm,400 nm和600 nm作为入射光波长。其中,200 nm对应深紫外光刻中使用的曝光波长范围,400 nm则代表实验室常用的紫外光刻的曝光波长范围,而600 nm则对应大学物理实验室中常用的氦氖激光器的波长范围。图2显示的是不同波长的入射光经过直径3 μm圆盘,在圆盘后3 μm处形成的衍射图像。从图中,我们可以看出,入射波长对泊松光斑影响明显。与理论预测的一致,当光波长越小时,衍射效果越弱。当入射光波长为200 nm时,只有在圆盘中心出现一个弱且小的泊松光斑,围绕着泊松光斑还有一些弱且密的高阶衍射圆环。随着入射光波长的增大,泊松亮斑的尺寸和强度都明显增加,围绕泊松亮斑的高阶衍射圆环的强度也增强,但衍射环数目减少。当入射光波长为600 nm时,圆盘遮挡区内只能观察到2个衍射圆环。在圆盘遮挡区之外,也能观察到明显的衍射条纹,其中离圆盘最近的零级衍射环的能量最高。衍射环之间的间距随着入射波长的增大而增加,随着远离圆盘而减小。

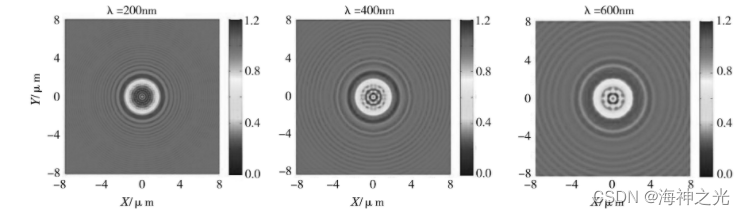
图2 不同波长的入射光经过直径3 μm圆盘,在圆盘后3 μm处形成的衍射图像

3 圆盘的尺寸对泊松亮斑的影响
我们将入射光的波长固定为400 nm,模拟了圆盘直径分别为2 μm,3 μm,4 μm时,在圆盘后3 μm处形成的衍射图像,显示在图3中。我们可以发现,随着圆盘直径的变大,泊松亮斑的光强度和直径明显减小,圆盘遮挡区的高阶衍射圆环强度降低,数目却相应增加。当圆盘直径为2 μm时,圆盘遮挡区已经没有高阶衍射圆环,只有一个暗环将泊松亮斑和0级衍射环分割开,0级衍射环和泊松亮斑的光场比较均匀。利用这个光场,配合正性的光刻胶和刻蚀工艺,可以实现纳米环的制备。而不同尺寸的圆盘在圆盘遮挡区外的衍射环间距基本相同,对比图2的结果,可以明显的推断出,圆盘遮挡区外的衍射环的间距与入射波长呈正比关系。

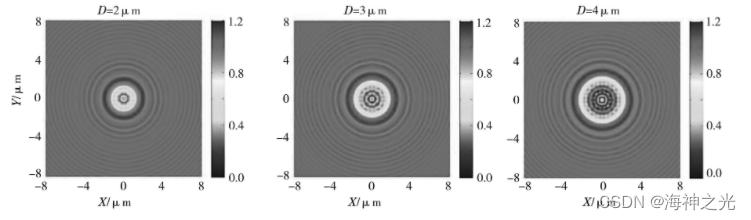
图3 入射波长为400 nm,圆盘直径分别为2 μm,3 μm,4 μm时,在圆盘后3 μm处形成的衍射图像

4 圆盘后不同距离对泊松亮斑的影响
我们将入射光的波长固定为400 nm,圆盘直径固定为3 μm,模拟了在圆盘后2 μm,3 μm,4 μm处形成的衍射图像,显示在图4中。从图中可知,随着衍射距离的增加,泊松亮斑的强度和直径都快速增加,圆盘遮挡区的高阶衍射圆环强度增加,数目则有所减少。在圆盘遮挡区外,不同尺寸的圆盘的衍射环间距也随着衍射距离的增加而有所增大。对比图2和图3的结果,可以推断出,圆盘遮挡区外的衍射环之间的间距不仅与入射波长呈正比关系,与圆盘后的衍射距离呈正相关特性。

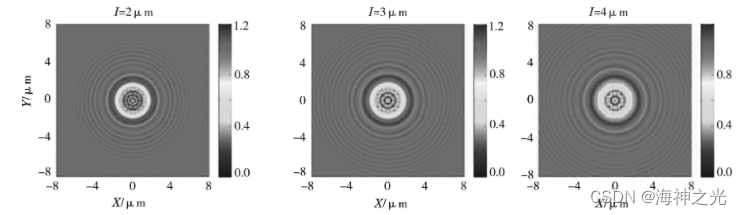
图4 入射波长为400 nm,圆盘直径为3 μm,圆盘后2 μm,3 μm,4 μm处形成的衍射图像

三、部分源代码

clear all;
clc;

% -----参数设定-----
M=512;
N=512; 
Lamda=0.6328; 
dx=2.0; 
dy=dx; 
HDiameter=32*dx; 
Zd=20.0e+3;

%-----输入形成泊松亮斑所需的圆孔函数-----
[x,y]=meshgrid(-dx*(M/2-1):dx:dx*M/2,-dy*(N/2-1):dy:dy*N/2);
Object=1-cyl(x,y,HDiameter); 
figure(1);
imshow(Object);

%-----进行衍射------


%-------显示衍射图样------
FrDiffract_I=abs(FrDiffract).^2.0;                           %计算衍射光场的强度分布

figure(2);
colormap(gray)
imshow(FrDiffract_IN,[0.1 0.1]);                               % 显示衍射图样的强度分布。 
% text_buffer =strcat('Diffraction patern at distance z=',num2str(Zd*1.0e-3),'mm ');%显示衍射距离。
% title(text_buffer);
% figure(3);
% imshow(FrDiffract_P);                                        % 显示衍射图样的相位分布。 
% title('Phase distribution of the diffraction field');

%------保存衍射图样的强度分布-----
imwrite(FrDiffract_IN,'Diffract_In.bmp');


  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
 

四、运行结果

五、备注

1 matlab版本
2014a

2 参考文献
[1] 门云阁.MATLAB物理计算与可视化[M].清华大学出版社，2013.
[2]赵靓,南香伶,张林海,张凌岳.泊松亮斑的模拟仿真研究[J].大学物理实验. 2020,33(01)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/125666270