2020 第十一届蓝桥杯大赛软件赛决赛，国赛，C/C++大学B组题解
【摘要】
文章目录
第1题——美丽的2 （5分）第2题——扩散 （5分）第3题——阶乘约数 （10分）第4题——本质上升序列 （10分）第5题——玩具蛇 （15分）第6题——皮亚诺曲线距离 （15分）第7题...
试题地址：https://www.lanqiao.cn/courses/2786/learning/?id=131138
补题地址：http://lx.lanqiao.cn/problemsets.page
第1题——美丽的2 （5分）
-
题目：
-
直接暴力1-2020，然后判断一下有没有2即可。
-
答案是563
#include<bits/stdc++.h> using namespace std; int main(){ int res = 0; for(int i = 1; i <= 2020; i++){ int x = i, cc = 0; while(x){ if(x%10==2)cc=1; x/=10; } if(cc)res++; } cout<<res<<"\n"; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
第2题——扩散 （5分）
-
题目
-
思路：
从四个点开始往外bfs，扩散2020轮即可。
对于坐标负数的情况，默认加上2020，相当于离散化处理。
注意边界处理 -
答案是20312088
#include<bits/stdc++.h> using namespace std; struct node{ int x, y, t = 0; }; int vis[2020+2020+2020][2020+2020+2020]; node getnode(int x, int y){ return node{x+2020,y+2020,0}; } int dx[] = {0,0,-1,1}; int dy[] = {1,-1,0,0}; int main(){ queue<node>q; q.push(getnode(0,0)); q.push(getnode(2020,11)); q.push(getnode(11,14)); q.push(getnode(2000,2000)); int ans = 0; while(q.size()){ node t = q.front(); q.pop(); vis[t.x][t.y] = 1; ans++; // cout<<t.x<<' '<<t.y<<" "<<t.t<<"\n"; // if(t.t==5)break; for(int i = 0; i < 4; i++){ int nx = t.x+dx[i], ny = t.y+dy[i]; if(vis[nx][ny]==0 && nx>=0&&ny>=0&&t.t+1<=2020){//边界 q.push({nx,ny,t.t+1}); vis[nx][ny] = 1; } } } cout<<ans<<"\n"; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
第3题——阶乘约数 （10分）
-
题目：
-
思路
由质因数唯一分解定理可得，100！分解质因数后表示唯一，所以的因数个数+1乘起来就是它的因数个数。所以直接枚举1-100，累加质因数，最后统计即可。
记得开ll不然会炸。 -
答案：39001250856960000
#include<bits/stdc++.h> using namespace std; int c[200]; int main(){ for(int i = 2; i <= 100; i++){ int x = i; for(int j = 2; j*j<=i; j++){ while(x%j==0){ x /= j; c[j]++; } } if(x!=1)c[x]++; } long long ans = 1; for(int i = 2; i <= 100; i++){ ans *= (c[i]+1); } cout<<ans<<"\n"; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
第4题——本质上升序列 （10分）
-
题目
-
思路：给出一个字符串，求有多少个不重复的单调递增子串
-
类似于最长上升子序列，区别在于不能重复，而且求的是个数。
记f[i]表示以s[i]结束的不重复单调递增子串个数，初始值为1即本身，转移时可以从前面所有比他小的字符转移过来，累加即可。
对于重复的情况，可以在转移时枚举到前面有和当前字符相同字符时把转移过的值记为0。 -
所以答案是3616159
#include<bits/stdc++.h> using namespace std; int f[500]; int main(){ string s="tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl"; for(int i = 0; i < s.size(); i++)f[i] = 1; for(int i = 0; i < s.size(); i++){ for(int j = 0; j < i; j++){ if(s[i]>s[j])f[i] += f[j]; if(s[i]==s[j])f[i] = 0; } } int ans = 0; for(int i = 0; i < s.size(); i++){ ans += f[i]; } cout<<ans<<"\n"; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
第5题——玩具蛇 （15分）
-
题目：
-
思路：
乍一看没啥头绪，但是考虑到只有16，方案数比较少，所以可以暴力dfs搜。
暴力每个起点，每次往四个方向搜+1，然后对于不同的终点答案+1。 -
所以答案是552
#include<bits/stdc++.h> using namespace std; int n = 4, ans = 0; int vis[10][10]; int dx[] = {0,0,-1,1}; int dy[] = {1,-1,0,0}; void dfs(int x, int y, int now){ if(now==n*n){ ans++; return ; } for(int i = 0; i < 4; i++){ int nx = x+dx[i], ny = y+dy[i]; if(nx>=1&&nx<=n&&ny>=1&&ny<=n &&vis[nx][ny]==0){ vis[nx][ny] = 1; dfs(nx,ny,now+1); vis[nx][ny] = 0; } } } int main(){ for(int i = 1; i <= n; i++){ for(int j = 1; j <= n; j++){ memset(vis,0,sizeof(vis)); vis[i][j] = 1; dfs(i,j,1); } } cout<<ans<<"\n"; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
第6题——皮亚诺曲线距离 （15分）
-
题目
-
思路：
说实话这道题目放在第六题感觉有点不讲武德，感觉比后面的难好吧（）
求两点距离不难想到可以转化为两点到起点的距离作差。 -
然后，考虑简化问题，k阶的图是由9个k-1阶的图组成的
我们可以考虑它在这九个中的哪一块，然后分类讨论递归下去，直到来到1阶和2阶，输出答案。#include<bits/stdc++.h> using namespace std; typedef long long LL; LL calc(LL x, LL n){ LL ans = 1; while(n){ if(n%2==1){ ans*=x; n--;} x *= x; n/= 2; } return ans; } LL dfs(LL now, LL xx, LL yy){ if(now==0)return 1; if(now>=40)now=39; //(n-1)阶时的边长，也就是n阶时，分成9个（n-1）阶时每一块的边长 LL k = calc(3,now-1); //判断该点在所在块内的横纵坐标(x,y)， 以及所在块的横纵坐标(a,b) LL x = xx%k, y = yy%k, a = xx/k, b = yy/k; if(a==0&&b==0) return 0*k*k+dfs(now-1,x,y); else if(a==0&&b==1)return 1*k*k+dfs(now-1,k-1-x,y); else if(a==0&&b==2)return 2*k*k+dfs(now-1,x,y); else if(a==1&&b==2)return 3*k*k+dfs(now-1,x,k-1-y); else if(a==1&&b==1)return 4*k*k+dfs(now-1,k-1-x,k-1-y); else if(a==1&&b==0)return 5*k*k+dfs(now-1,x,k-1-y); else if(a==2&&b==0)return 6*k*k+dfs(now-1,x,y); else if(a==2&&b==1)return 7*k*k+dfs(now-1,k-1-x,y); else if(a==2&&b==2)return 8*k*k+dfs(now-1,x,y); } int main(){ LL n; cin>>n; LL x1, y1, x2, y2; cin>>x1>>y1>>x2>>y2; LL ans = dfs(n,x1,y1)-dfs(n,x2,y2); if(ans<0)ans=-ans; cout<<ans<<"\n"; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
第7题——游园安排 （20分）
-
题目
-
思路：
看完就是个LIS最长上升子序列，只不过把数字换成了字符串比较。
对于路径打印，开个数组回溯一下即可。
暴力dp能过70%//70分做法 #include<bits/stdc++.h> using namespace std; const int maxn = 1e6+10; int cnt = 0; string name[maxn]; int f[maxn]; //到i为止的最大值 int main(){ string s; cin>>s; for(int i = 0; i < s.size(); i++){ if(isupper(s[i])){ name[++cnt]=""; name[cnt]+=s[i]; }else{ name[cnt]+=s[i]; } } int mxl = 0, pos = 1; //记录最长序列的长度和坐标 for(int i = 1; i <= cnt; i++){ f[i] = 1; for(int j = 1; j < i; j++){ if(name[i]>name[j]){//可以从比i小的转移过来 f[i] = max(f[i], f[j]+1); } } if(f[i]>=mxl){ mxl = f[i], pos = i; } } string res = ""; for(int i = pos; i >= 1; i--){//向前回溯 if(f[i]==mxl){ res = name[i]+res; mxl--; } } cout<<res<<"\n"; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
-
考虑贪心优化
将所有人序列取出存储到数组中后，先将第一个序列入队，遍历剩下所有序列，如果说碰见比队尾大的序列就直接入队，否则，也就是当前序列并不小于队尾序列的话，那么就用其代替掉队列中比其大的第一个序列，至于如何找到这个第一个比他大的，因为队列是有序的，那么就可以二分，复杂度从平方优化到了log。#include<bits/stdc++.h> using namespace std; const int maxn = 1e6+10; #define IOS ios::sync_with_stdio(0), cin.tie(0),cout.tie(0) int cnt = 0; string name[maxn]; vector<int>f; //到i为止的最大值 int main(){ IOS; string s; cin>>s; for(int i = 0; i < s.size(); i++){ if(isupper(s[i])){ if(i!=0)cnt++; name[cnt]=""; name[cnt]+=s[i]; }else{ name[cnt]+=s[i]; } } vector<string>vc; //当前LIS序列 vc.push_back(name[0]); f.push_back(1); for(int i = 1; i <= cnt; i++){ if(name[i] > vc.back()){//能构成就直接加 vc.push_back(name[i]); f.push_back(vc.size()); }else{//不能就去二分第一个小于name[i]的位置替换掉（肯定更优） int pos = lower_bound(vc.begin(), vc.end(), name[i])-vc.begin(); vc[pos] = name[i]; f.push_back(pos+1); } } // string res = ""; vector<string>res; int len = vc.size(); for(int i = cnt; len>0; i--){//向前回溯 if(f[i]==len){ res.push_back(name[i]); // res = name[i]+res; len--; } } // cout<<res<<"\n"; for(int i = res.size()-1; i >= 0; i--){ cout<<res[i]; } return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
第8题——答疑 （20分）
- 题目
- 思路：
贪心策略为，a+s+e越小的排在越前面。证明过程参考如下。https://blog.csdn.net/AC__dream/article/details/124025236
#include<bits/stdc++.h> using namespace std; struct node{ int s, a, e; }p[1500]; bool cmp(node x, node y){ return x.s+x.a+x.e<y.s+y.a+y.e; } int main(){ int n; cin>>n; for(int i = 1; i <= n; i++) cin>>p[i].s>>p[i].a>>p[i].e; sort(p+1,p+n+1,cmp); long long ans = 0; for(int i = 1; i <= n; i++){ ans += (n-i)*(p[i].a+p[i].e+p[i].s)+p[i].a+p[i].s; } cout<<ans<<"\n"; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
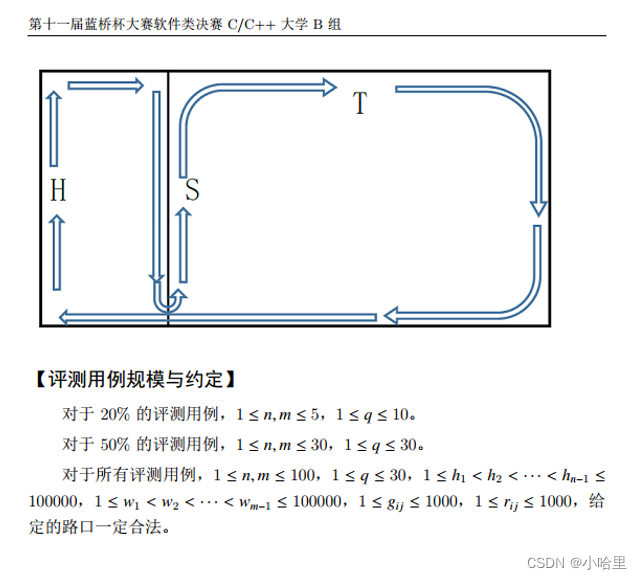
第9题——出租车 （25分）
-
题意：
-
思路：
最短路，Dijkstra或spfa，代码太长不想写了，
贴个其他dalao的题解把
https://zhuanlan.zhihu.com/p/441856768
https://blog.csdn.net/l961983207/article/details/122813788
第10题——质数行者 （25分）
- 题意：
- 思路
oh，高维dp，不想写了
贴个其他dalao的题解把
https://blog.csdn.net/qq_36213882/article/details/123380736
文章来源: gwj1314.blog.csdn.net，作者：小哈里，版权归原作者所有，如需转载，请联系作者。
原文链接：gwj1314.blog.csdn.net/article/details/125065084
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）