【图像去噪】基于matlab正则化图像去噪【含Matlab源码 1891期】
一、正则化图像去噪简介
1 稀疏性正则化的去噪模型
记u={ui, j:i, j=1, …, N}为原始理想图像, z={zi, j:i, j=1, …, N}为被泊松噪声污染后的噪声图像, 图像z中每一个像素zi, j皆为独立且均值为ui, j的Poisson随机变量的实现.依据泊松分布的定义, 要求均值ui, j>0.因此给定理想图像u时, 观测图像z的泊松似然概率分布为:
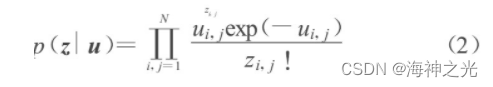
借助于信号在冗余字典下的线性展开 (1) , 似然概率分布可改写为:
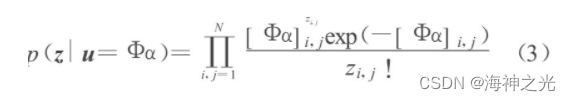
图像去噪的任务是从观测图像z恢复出理想图像u, 由于用于问题求解的信息量不足, 这是一个不适定 (ill-posed) 的反问题.在Bayesian统计框架下充分利用理想图像的先验知识有利于改善问题性质.基于图像u在冗余字典φ下的稀疏表示先验知识, 假设稀疏表示系数{αi}i∈I相互独立, 且系数α应满足如下的Gibbs分布:
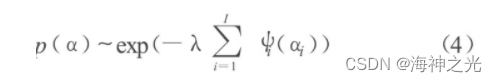

第一项为泊松似然分布, 第二项为系数α的先验分布.为了符合泊松分布均值非负的特性, 应增加对φα (均值) 的非负性约束.进一步将式 (3) 与式 (4) 代入并简化后, 式 (5) 可表示为:
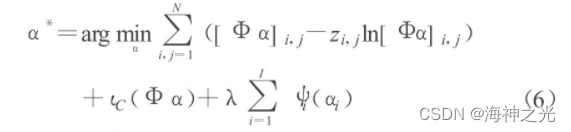
其中, {ψi (αi) }i∈I为稀疏性惩罚函数, I={1, …, I} (I∈N) , ιC为凸集C的示性函数, 定义为:
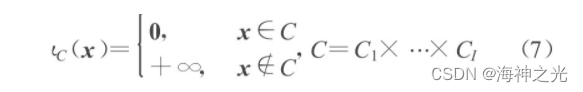
为了符合泊松分布均值非负的特性, 选取凸集C1≤i≤I={x∈L2 ® x}≥0}, 约束均值φα的非负性, 从而也保证了去噪后图像灰度值的非负性.目标泛函中综合了关于原子系数的稀疏性约束和数据保真信息, λ为正则化参数, 在正则项与保真项之间相互权衡, 最小化此能量目标泛函, 可恢复理想图像为

为了重建模型的便于求解, 要求稀疏性惩罚函数{ψi (αi) }i∈I为闭的下半连续凸函数.同时为了有效度量框架系数的稀疏性, 要求其满足下面的条件:
ψi为偶对称的连续非负函数, 在[0, +∞) 上非递减, 且ψi (0) =0 (i∈I)
但对其并无光滑性要求, 从而可选择更为广泛的稀疏性惩罚函数.其实, 当前广泛采用的稀疏性惩罚函数通常是非光滑的, 如l1范数.
目标泛函 (6) 中每一项关于问题变量α均是凸的, 因而整个式 (6) 为凸变分模型, 同时也是强制的 (coercive) , 因此变分问题 (6) 的解一定存在.如果进一步ψ1≤i≤I为严格凸函数, 则目标泛函为严格凸的, 从而变分问题 (6) 存在唯一解.
二、部分源代码
- 1
三、运行结果

四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社,2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社,2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社,2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社,2015.
[5]孙玉宝,韦志辉,吴敏,肖亮,费选.稀疏性正则化的图像泊松去噪算法[J].电子学报. 2011,39(02)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/125321109
- 点赞
- 收藏
- 关注作者


评论(0)