【轴承故障分解】基于matlab ITD轴承故障信号分解【含Matlab源码 1871期】

一、ITD轴承故障信号分解简介

滚动轴承局部损伤故障振动信号多为非平稳的多分量调制信号, 采用合适的时频分析方法将故障信号分解为若干个单分量AM-FM信号, 再对其包络解调是轴承故障诊断的常用手段。本征时间尺度分解 (Intrinsic Time-Scale Decomposition, ITD) 是针对传统时频分析方法的局限性提出的新方法, 可自适应性地将一个复杂信号分解为若干个合理旋转 (Proper Rotation, PR) 分量之和, 每个PR分量通过一次迭代即可获得, 端点效应小, 分解能力强, 计算速度明显优于经验模态分解 (Empirical Mode Decomposition, EMD) 和局部均值分解 (Local Mean Decomposition, LMD) 方法, 有利于实现在线故障诊断。

1 ITD方法
1.1 原理
设待分解信号Xt的极值为Xk, 对应时刻为τk (k=1, 2, …, N, N为所有极值点个数) 。定义L为基线提取算子, Lt=LXt为信号的基线分量, 则Xt被分解为Xt=Lt+Ht, Ht为待提取的PR分量。
(1) L通过相邻基线控制点Lk和Lk+1在[τk, τk+1] (k=1, 2, …, N) 上对Xt线性变换所得, 即

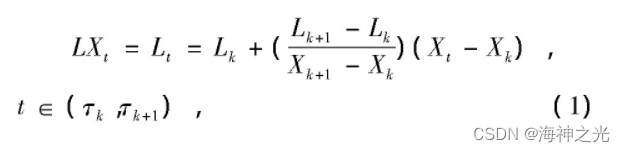
其中每个基线控制点为

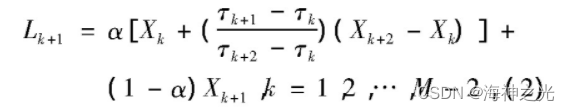
式中:α为线性增益, 一般取0.5。

(2) 定义一个固有旋转分量提取算子LXt, 则

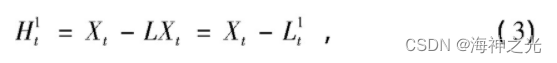
式中:Ht1为分离出来的最高频率的PR分量。然后将Lt1作为原始信号, 重复上述步骤, 直到基线信号Ltp为一单调或常函数, 原始信号被分解为

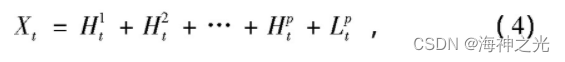
式中:Hti为第i个PR分量;Ltp为第p次分解后的残余分量。

ITD方法中的基线通过信号的线性变换得到, 避开了EMD方法中求极大值和极小值包络时使用的两次、三次样条拟合, 从而缩短计算时间, 减少拟合误差, 所以ITD方法端点效应小且计算速度快。

1.2 新迭代终止条件
由上述原理可知, ITD方法进行PR分量分解的迭代终止条件为基线信号Ltp为一单调或常函数。原始信号各分量的信息主要集中在前几个能量较高的PR分量中, 尤其当存在噪声成分时, 后几个PR分量为无意义的受干扰分量。为进一步减少计算量, 加快分解速度, 从能量角度出发提出ITD方法的新迭代终止条件。

二、部分源代码

function [H,L]=Itd(x,n,err)
% 将信号x进行ITD分解
% n分解层数 自己设定的最大的分解层 若没有这么多次 也会自动停止
% err 为常函数的值小于这个值的时候停止
%--------------------------
if nargin==1   %输入变量个数
    n=3;
    err=0.05;
end
if nargin==2
    err=0.05;
end
 [tempH1,tempL]= Intrinsic_timescale_decomposition(x);
 H=tempH1;
H=[];
for i=1:n
    [tempH,tempL]= Intrinsic_timescale_decomposition(x);
    H=[H;tempH]; %行矩阵
    %----终止条件
    %有两个终止条件 一个是基线信号为单调函数 一个是常函数
    if dandiao(tempL)==1 %单调函数
        break;
    end
    if max(tempL)<err && abs(min(tempL))<err %常函数 正负数的绝对值都要满足即绝对值在err之间
        break;
    end
    x=tempL;
    %-------
end
L=tempL;
end
function rlt=dandiao(xx)
% 求是否单调函数
x1=diff(xx);
rlt=0;
if all(x1>=0) || all(x1<=0)
    rlt=1;
end
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社，2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社，2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社，2018.
[4]唐贵基,庞彬.基于ITD和切片双谱的滚动轴承局部损伤故障诊断[J].轴承. 2014,(08)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/125247164