【图像融合】基于matlab OpenSUFT红外与可见光配准融合【含Matlab源码 1878期】

一、SIFT配准简介

1 图像配准
SIFT是David Lowe于1999年提出的局部特征描述子。SIFT算法是一种提取局部特征的算法,也是一种模式识别技术,其基本思想是在尺度空间寻找极值点,提取位置、尺度、旋转不变量。它主要包括两个阶段,一个是SIFT特征的生成,即从多幅图像中提取对尺度缩放、旋转、亮度变化无关的特征向量;第二阶段是SIFT特征向量的匹配。SIFT算法的主要特点:

1. SIFT特征是图像的局部特征,其对旋转、尺度缩放、亮度变化、视角变化、仿射变换、噪声都保持一定程度的稳定性。
2. 独特性好,信息量丰富,适用于在海量特征数据库中进行快速、准确的匹配。
3. 多量性,即使少数的几个物体也可以产生大量SIFT特征向量。
4. 高速性,经优化的SIFT匹配算法甚至可以达到实时的要求。
5. 可扩展性,可以很方便地与其他形式的特征向量进行联合。

1.1 SIFT算法实现

1. 特征点检测
   实际图像中的特征角点常发生在不同的尺度范围上,并且每一角点的尺度信息是未知的。一般认为在较大尺度下能较可靠地消除误检和检测到真正的角点,但角点的定位不易准确。相反,在较小尺度下对真正的特征角点的定位比较准确,但误检的比例会增加。所以,可考虑先在较大尺度下检测出角点,然后在较小尺度下对真正特征角点进行较精确定位。因此,本文利用多尺度技术检测角点。

2. 特征点描述(即建立特征向量)
   每个关键点设定三个信息:位置、尺度、方向。在以特征点为中心的邻域窗口内采样,并用梯度方向直方图来统计邻域像素的梯度方向。在实际计算过程中,为了增强匹配的稳健性,Lowe建议对每个关键点使用4×4共16个种子点来描述,这样对于一个关键点就可以产生128个数据,即最终形成128维的SIFT特征向量。此时SIFT特征向量已经去除了尺度变化、旋转等几何变形因素的影响,再继续将特征向量的长度归一化,则可以进一步去除光照变化的影响。

3. 进行特征匹配以获得候选匹配点
   这一步根据特征向量的相似性来进行匹配,一般采用各种距离函数作为特征的相似性度量,如欧氏距离(Euclidean Distance)、街区距离(Block Distance)、马氏距离(Mahalanobis Distance)等。

4. 消除错配
   无论采用何种特征描述符和相似性判定度量,错配难以避免。这一步主要做的就是根据几何或光度的约束信息去除候选匹配点中的错配。常用的方法是RANSAC随机抽样一致性算法[6],常用的几何约束是极线约束关系(Epipolar Line)。

2.2 配准过程

1. 图像预处理
   原始可见图像如图1所示。由于红外图像是物体自身辐射所形成的,反映的是物体自身辐射的能力,如光滑的表面发射率较低,粗糙的表面发射率较高,因此图像一般比较暗,边缘模糊,整幅图像噪声较大,信噪比低,纹理较弱,如图2所示。在本文中,我们先对图像进行二值化,然后在二值图像基础上做的SIFT变换,二值图像匹配的特征点如图3所示。
2. 使用上述SIFT算法提取特征点。
3. 计算变换参数。
   有学者使用仿射变换的方法,来表示两幅图像的变换关系。仿射变换模型可以表示为
   
   式中(x,y),(x′,y′)分别是两幅图像中对应点的坐标。仿射变换是以6个参数决定两幅图像坐标之间的变换关系。

在本文中,我们使用了透视变换(Perspective Transformation)的方法。透视变换模型可以表示为

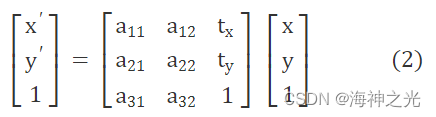
可以看到,透视变换是以8个参数决定的两幅图像坐标之间的变换关系。
利用透视中心、像点、目标点三点共线的条件,按透视旋转定律使承影面(透视面)绕迹线(透视轴)旋转某一角度,破坏原有的投影光线束,仍能保持承影面上投影几何图形不变换。对比两种变换的定义可知,透视变换比仿射变换更加精准。两幅图像由于成像原理、视角、焦距、光照等因素的影响,图像的平行关系不一定保持,所以,它们之间的变换更符合透视变换。
本文使用的插值方法是线性插值法。
仿射变换的数学描述:

透视变换的数学描述:

图4所示为仿射变换后的红外图像,图5所示为透视变换后的红外图像。由图4、5可以看出,仿射变换后的图像明显有些变形,透视变换比仿射变换更加有效。

2 基于HSI空间的图像融合
HSI色彩空间是从人的视觉系统出发,用色调(Hue)、饱和度(Saturation或Chroma)和亮度(Intensity或Brightness)来描述色彩。HSI色彩空间可以用一个圆锥空间模型来描述。这种描述HSI色彩空间的圆锥模型相当复杂,但是却能把色调、亮度和色饱和度的变化情形表现得很清楚。

基于HSI空间的变换算法较为简单、程序运行效率很高,且不容易产生分块效应[3],有利于工程实现。因此,本文采用基于HSI空间的融合方法[8],一般步骤如下:

1. 将多光谱图像的R、G、B三个波段转换到HSI空间,得到H、S、I三个分量。
2. 将全色图像与多光谱图像经HSI变换后得到亮度分量I,在一定的融合规则下进行融合,得到新的亮度分量(融合分量)。
3. 用第2)步得到的融合分量代替亮度分量图像,并同H、S分量图像一起转换到RGB空间,最后得到融合结果图像。
   在上述步骤中,第2)步的融合规则可以选取不同的融合方法,如直接替换法、加权平均法、直方图匹配法等。本文考虑到融合权值的调节,采用了加权平均法进行融合,如图6、7所示。

二、部分源代码

% 载入图像  
%%%发现只有匹配点对遍布在图像中，匹配效果才会变好  
I11=(imread('image/qa1.bmp'));%红外图像  
I22=(imread('image/qa2.bmp'));%可见光图像  
I10=rgb2gray(I11);  
I20=rgb2gray(I22);  
I1=imadjust(I10);  
I2=imadjust(I20);  
%边缘检测
I1 = im2double(edge(I1,'canny'));   
I2 = im2double(edge(I2,'canny'));   
figure,imshow(I1);  
figure,imshow(I2);  
  
% 获取特征点
Options.upright=true;  
Options.tresh=0.0001;  
Ipts1=OpenSurf(I1,Options);  %1*268  
Ipts2=OpenSurf(I2,Options);  

% 将特征点描述子放入一个矩阵 
D1 = reshape([Ipts1.descriptor],64,[]);  %64*268  
D2 = reshape([Ipts2.descriptor],64,[]);  
  
% 找到最佳匹配
err=zeros(1,length(Ipts1));     
cor1=1:length(Ipts1);  
cor2=zeros(1,length(Ipts1));  
for i=1:length(Ipts1)  
    distance=sum((D2-repmat(D1(:,i),[1 length(Ipts2)])).^2,1);%用D2的每一列分别去减D1的每一列  
    [err(i),cor2(i)]=min(distance);  
end  

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.
[5]李健,王滨海,李丽,张晶晶.基于SIFT的电力设备红外与可见光图像的配准和融合[J].光学与光电技术. 2012,10(01)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/125255175