线性表的链式存储结构
3.6线性表的链式存储结构
3.6.1.顺序存储结构不足的解决方法
线性表的顺序存储结构是有缺点的,最大的缺点就是插入和删除时需要移动大量元素,这显然就需要耗费时间。能不能想办法解决呢?
要解决这个问题,我们就得考虑一下导致这个问题的原因:
为什么当插入和删除时,就要移动大量元素,仔细分析后,发现原因就在于相邻两元素的存储位置也具有邻居关系。它们编号是1,2,3,…,n,它们在内存中的位置也是挨着的,中间没有空隙,当然就无法快速介入,而删除后,当中就会留出空隙,自然需要弥补。问题就出在这里。
想法一:让当中每个元素之间都留有一个空位置,这样要插入时,就不至于移动。可一个空位置如何解决多个相同位置插入数据的问题呢?所以这个想法显然不行。
想法二:那就让当中每个元素之间都留足够多的位置,根据实际情况制定空隙大小,比如10个,这样插入时,就不需要移动了。万一10个空位用完了,再考虑移动使得每个位置之间都有10个空位置。如果删除,就直接删掉,把位置留空即可。这样似乎暂时解决了插入和删除的移动数据问题。可这对于超过10个同位置数据的插入,效率上还是存在问题。对于数据的遍历,也会因为空位置太多而造成判断时间上的浪费。而且显然这里空间复杂度还增加了,因为每个元素之间都有若干个空位置。
想法三:我们反正也是要让相邻元素间留有足够余地,那干脆所有的元素都不要考虑相邻位置了,哪有空位就到哪里,而只是让每个元素知道它下一个元素的位置在哪里,这样,我们可以在第一个元素时,就知道第二个元素的位置(内存地址),而找到它;在第二个元素时,再找到第三个元素的位置(内存地址)。这样所有的元素我们就都可以通过遍历而找到。
显而易见,第三种想法是我们今天讨论的主线。
3.6.2.线性表链式存储结构定义
先上图:

线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的。这就意味着,这些数据元素可以存在内存未被占用的任意位置。
在顺序结构中,每个数据元素只需要存数据元素信息就可以了。现在在链式结构中,除了要存数据元素外,还要存储它的后级元素的存储地址。所以,对数据元素 ai 来说,除了存储其本身的信息之外,还需存储一个指示其直接后继的信息(即直接后继的存储位置)。我们把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。指针域中存储的信息称作指针或链。这两部分信息组成数据元素 ai 的存储映像,称为结点(Node)。
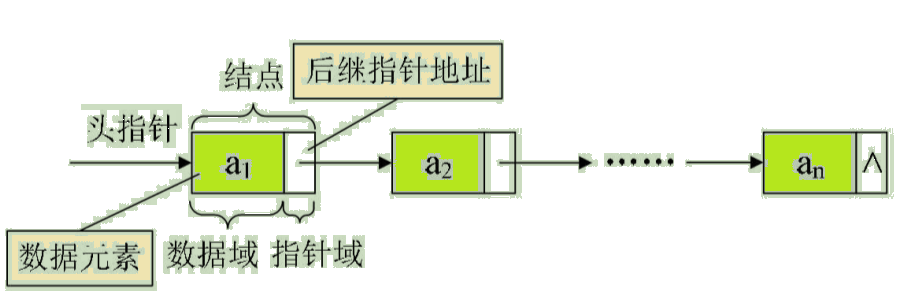
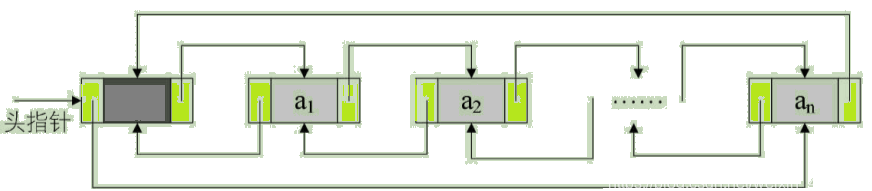
n个结点链接构成一个链表,即为线性表(a1,a2, … ,an)的链式存储结构,因为此链表的每个结点中只包含一个指针域,所以叫做单链表。单链表正式通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起,如图:
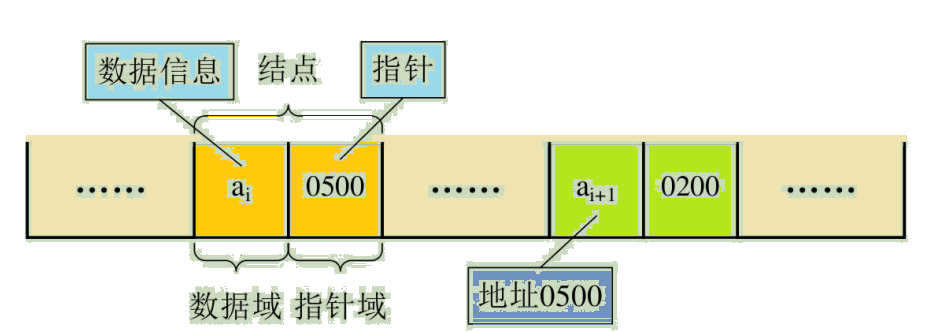
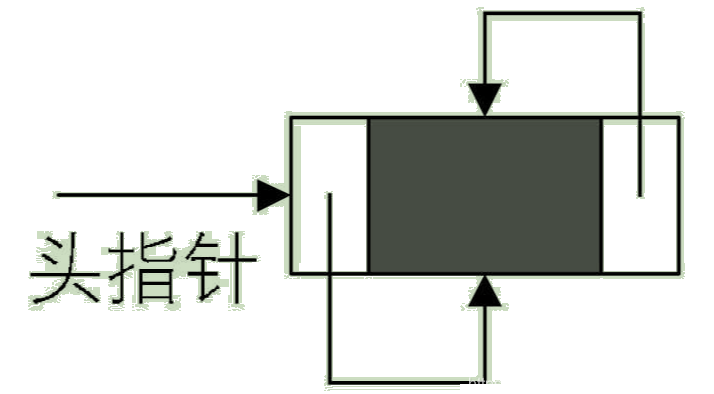
对于线性表来说,总得有个头有个尾,链表也不例外。我们把链表中第一个结点的存储位置叫做头指针,那么整个链表的存取就必须是从头指针开始进行了。之后的每一个结点,其实就是上一个的后继指针指向的位置。线性链表的最后一个结点指针为“空”(通常用NULL或^表示)。
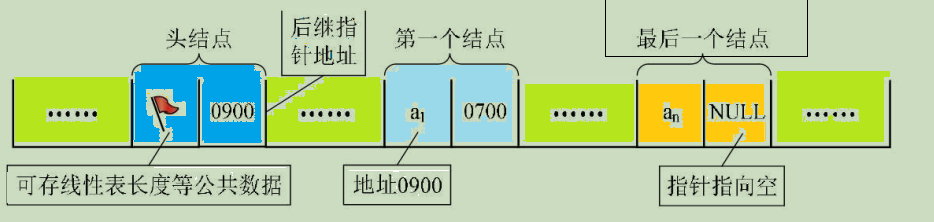
有时,我们为了更加方便地对链表进行操作,会在单链表的第一个结点前附设一个结点,称为头结点。头结点的数据域可以不存储任何信息,也可以存储如线性表的长度等附加信息,头结点的指针域存储指向第一个结点的指针,如图:
3.头指针与头结点的异同
又是头指针又是头结点,这都是啥啊,别着急!看图:

这回,明白了吧,嘿嘿,我们继续学习~~
4.线性表链式存储结构代码描述
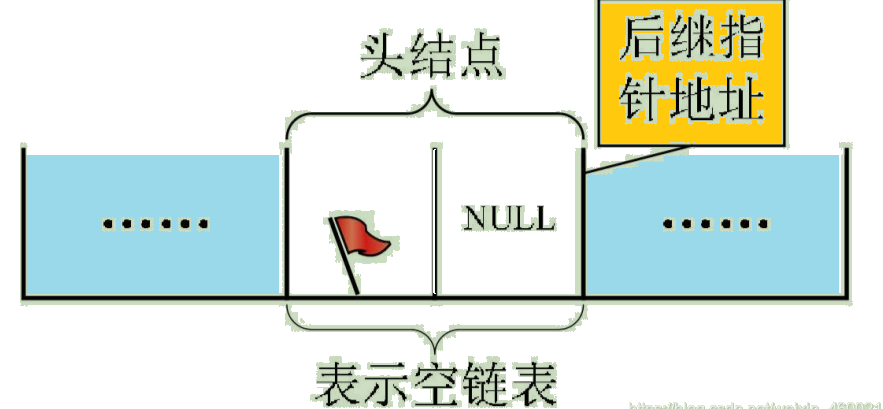
若线性表为空,则头结点的指针域为空,如图:
接下来我们再来看一下一般的单链表的图示:
在这里插入图片描述
用代码来表示一下单链表:
/* 线性表的单链表存储结构 */
typedef struct Node
{
/* 数据域 */
ELemType data;
/* 指针域 */
struct Node *next;
} Node;
/* 定义LinkList */
typedef struct Node *LinkList;
从这个结构定义中,我们也就知道,结点由存放数据元素的数据域和存放后继结点地址的指针域组成。假设p是指向线性表第i个元素的指针,则该结点 ai 的数据域我们可以用 p->data 来表示,p->data的值是一个数据元素,结点 ai 的指针域可以用 p->next 来表示,p->next 的值是一个指针。p->next 指向谁呢?当然是指向第 i+1 个元素,即指向 ai+1 的指针。也就是说,如果 p->data = ai,那么 p->next->data = ai+1,请看图:
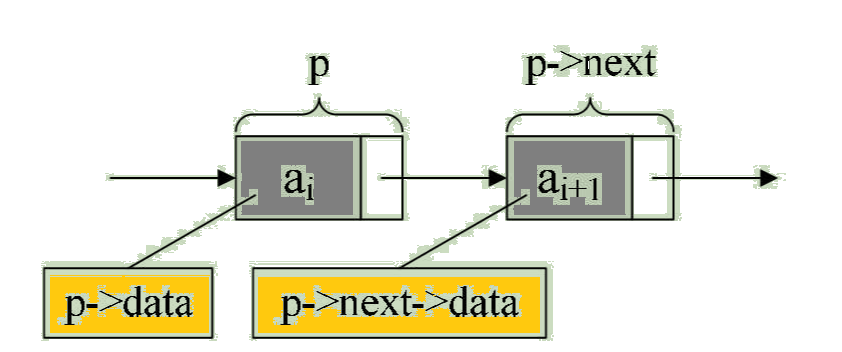
1.单链表的读取
在线性表的顺序存储结构中,我们要计算任意一个元素的存储位置是很容易的。但在单链表中,由于第i个元素没办法一开始就知道,必须得从头开始找。
获得链表第 i 个数据的算法思路:
声明一个指针 p 指向链表第一个结点,初始化 j 从 1 开始;
当 j < i 时,就遍历链表,让 p 的指针向后移动,不断指向下一个结点,j 累加 1;
若到链表末尾 p 为空,则说明第 i 个结点不存在;
否则查找成功,返回结点 p 的数据。
/* 初始条件:顺序线性表 L 已经存在,1 <= i <= ListLength(L) */
/* 操作结果:用 e 返回 L 中第 i 个数据元素的值 */
Status GetElem(LinkList L, int i, ElemType *e)
{
int j;
LinkList p; /* 声明一指针 p */
p = L->next; /* 让 p 指向链表 L 的第一个结点(有头结点的话就是指向头结点) */
j = 1; /* j 为计数器 */
/* p 不为空且计数器 j 还没有等于 i 时,循环继续 */
while (p && j < i)
{
p = p->next; /* 让 p 指向下一个结点 */
++j;
}
if (!p || j > i)
return ERROE /* 第 i 个结点不存在 */
*e = p->data; /* 取第 i 个结点的数据 */
return OK;
}
说白了,就是从头开始找,直到第 i 个结点为止。由于这个算法的时间复杂度取决于 i 的位置,当 i = 1 时,则不需遍历,当 i = n 时则遍历 n - 1 次才可以。因此最坏情况的时间复杂度是 O(n)。
由于单链表的结构中没有定义表长,所以不能事先知道要循环多少次,因此也就不方便使用for来控制循环。其主要核心思想就是“工作指针后移”,这其实也是很多算法的常用技术。
2.单链表的插入
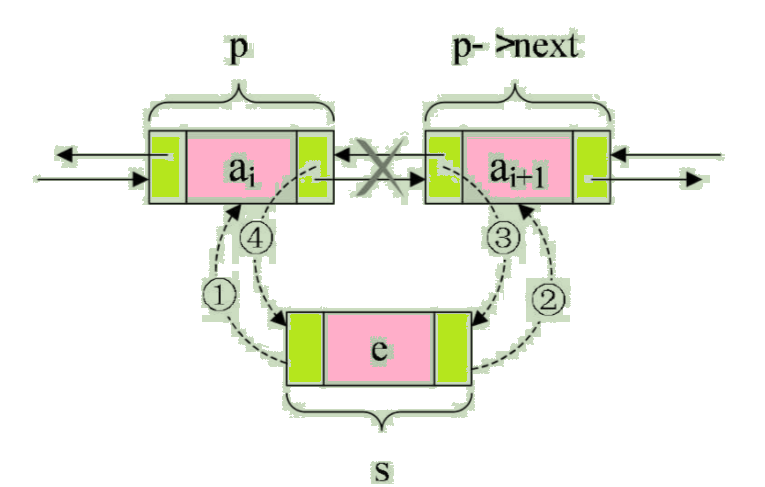
假设存储元素 e 的结点为 s,要实现结点 p 、p->next 和 s之间逻辑关系的变化,只需将结点 s 插入到结点 p 和 p->next之间即可。如图:
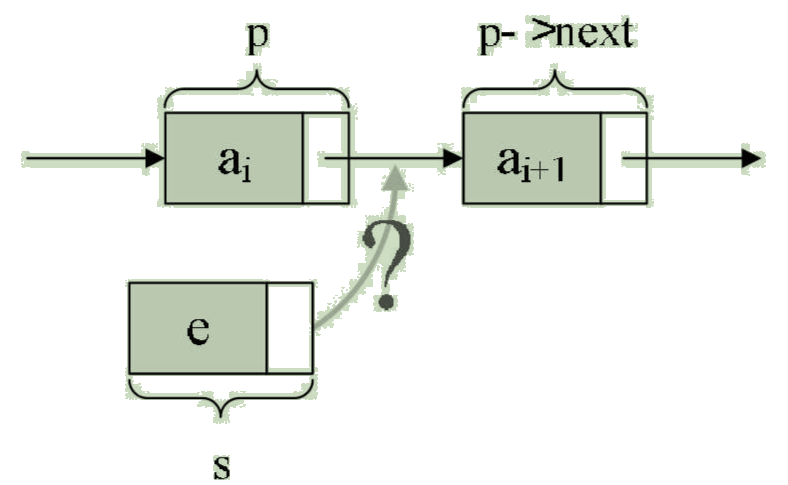
可以发现,只需让 s->next 和 p->next 的指针做一点改变即可。
s->next = p->next; /* 让p的后继结点改成s的后继结点 */
p->next = s; /* 把结点s变成p的后继结点 */
三遍定律:
两句的顺序不可以交换!
两句的顺序不可以交换!
两句的顺序不可以交换!
那接下来我们看看为啥交换不得:
如果先p->next=s;再s->next=p->next;会怎么样?哈哈,因为此时第一句会使得将p->next给覆盖成s的地址了。那么s->next=p->next,其实就等于s->next=s。这样真正的拥有ai+1数据元素的结点就没了上级。这样的插入操作就是失败的,造成了临场掉链子的尴尬局面。
正确插入后是这样的。如图:
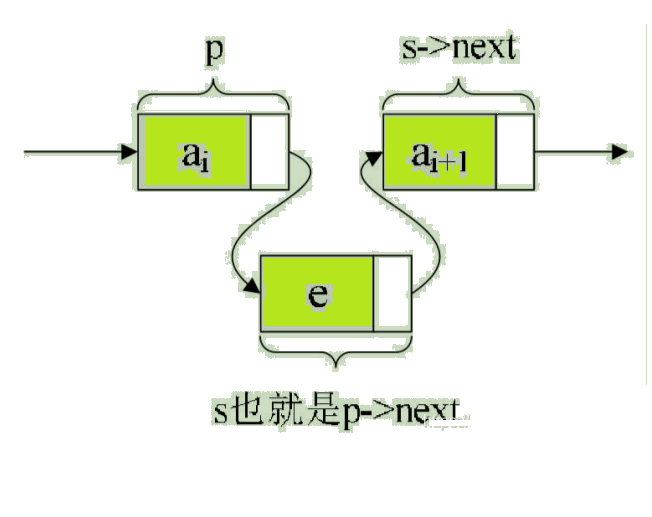
单链表第i个数据插入结点的算法思路:
1.声明一指针 p 指向链表头结点,初始化 j 从1 开始;
2.当 j < i 时,就遍历链表,让 p 的指针向后移动,不断指向下一结点,j 累加 1;
3.若到链表末尾 p 为空,则说明第 i 个结点不存在;
4.否则查找成功,在系统中生成一个空结点s;
5.将数据元素 e 赋值给 s->data;
6.单链表的插入标准语句 s->next = p->next; p->next = s;
7.返回成功。
算法代码如下:
/* 初始条件:顺序线性表 L 已经存在,1 <= i <= ListLength(L) */
/* 操作结果:在 L 中第 i 个结点位置之前插入新的数据元素 e,L 的长度增加 1 */
Status ListInsert(LinkList *L, int i, ElemType e)
{
int j;
LinkList p, s;
p = *L;
j = 1;
/* 寻找第 i-1 个结点 */
while (p && j < i)
{
p = p->next;
++j;
}
/* 第 i 个结点不存在 */
if (!p || j > i)
return ERROR;
/* 生成新的结点(C标准函数) */
s = (LinkList)malloc(sizeof(Node));
s->data = e;
/* 将 p 的后继结点赋值给 s 的后继 */
s->next = p->next;
/* 将 s 赋值给 p 的后继 */
p->next = s;
return OK;
}
malloc : C语言标准函数,它的作用就是生成一个新的结点,其类型与 Node 是一样的,其实实质就是在内存中找了一小块儿空地,准备用来存放数据 e 的 s 结点。
3.单链表的删除
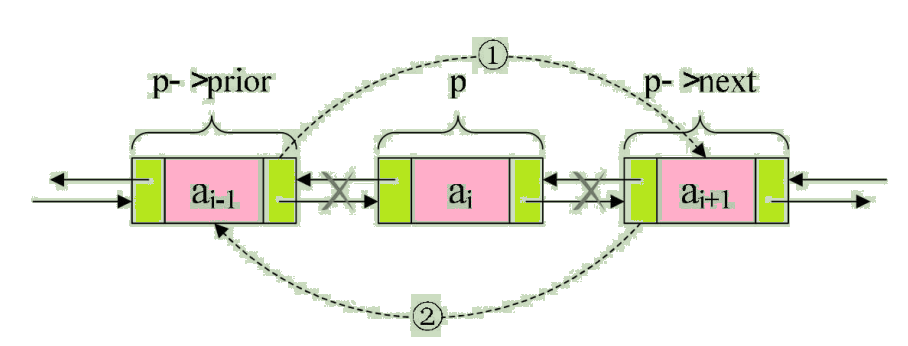
设存储元素 ai 的结点为 q,要实现将结点 q 删除单链表的操作,其实就是将他的前驱结点直接指向它的后继结点。如图:
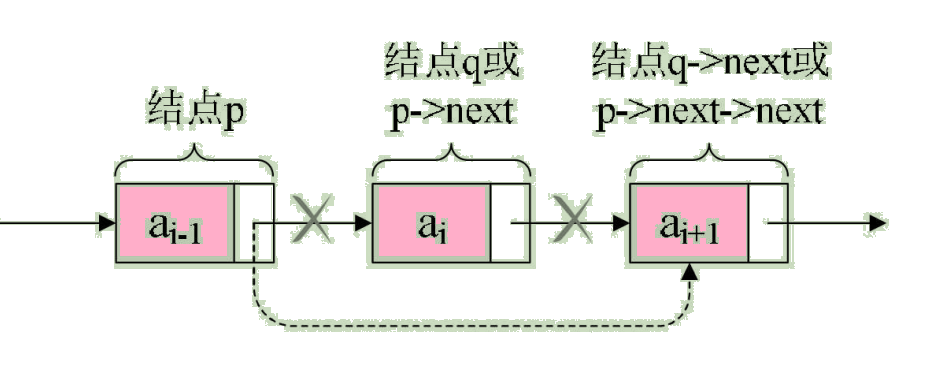
我们所要做的,实际上就是一步,p->next=p->next->next,用q来取代p->next,即是:
q=p->next; p->next=q->next;
单链表第i个数据删除结点的算法思路:
1.声明一指针 p 指向链表头结点,初始化 j 从 1 开始;
2.当 j < i 时,就遍历链表,让 p 的指针向后移动,不断指向下一个结点,j 累加 1;
3.若到链表末尾 p 为空,则说明第 i 个结点不存在;
4.否则查找成功,将欲删除的结点 p->next 赋值给 q;
5.单链表的删除标准语句 p->next = q->next;
6.将 q 结点中的数据赋值给 e,作为返回;
7.释放 q 结点;
8.返回成功。
算法代码如下:
/* 初始条件:顺序线性表 L 已经存在,1 <= i <= ListLength(L) */
/* 操作结果:在 L 中第 i 个结点位置之前插入新的数据元素 e,L 的长度增加 1 */
Status ListInsert(LinkList *L, int i, ElemType e)
{
int j;
LinkList p, q;
p = *L;
j = 1;
/* 遍历寻找第 i - 1 个结点 */
while (p->next && j < i)
{
p = p-> next;
++j;
}
/* 第 i 个结点不存在 */
if (!(p->next) || j > i)
return ERROR;
q = p->next;
/* 将 q 的后继赋值给 p 的后继 */
p->next = q->next;
/* 将 q 结点中的数据给 e */
*e = q->data;
/* 让系统回收此结点,释放内存 */
free(q)
return OK;
}
free : 作用是让系统回收一个 Node 结点,释放内存。
分析一下上面的单链表插入和删除算法,我们发现,它们其实都是由两部分组成:第一部分就是遍历查找第i个结点;第二部分就是插入和删除结点。
从整个算法来说,我们很容易推导出:它们的时间复杂度都是O(n)。如果在我们不知道第i个结点的指针位置,单链表数据结构在插入和删除操作上,与线性表的顺序存储结构是没有太大优势的。但如果,我们希望从第i个位置,插入10个结点,对于顺序存储结构意味着,每一次插入都需要移动n-i个结点,每次都是O(n)。而单链表,我们只需要在第一次时,找到第i个位置的指针,此时为O(n),接下来只是简单地通过赋值移动指针而已,时间复杂度都是O(1)。显然,对于插入或删除数据越频繁的操作,单链表的效率优势就越是明显。
4.单链表的整表创建
顺序存储结构的创建,其实就是一个数组的初始化,即声明一个类型和大小的数组并赋值的过程。而单链表和顺序存储结构不同。对于每个链表来说,它所占用空间的大小和位置是不需要预先分配划定的,可以根据系统的情况和实际的需求即时生成。
创建单链表的过程就是一个动态生成链表的过程。即从“空表”的初始状态起,依次建立各元素结点,并逐个插入链表。
单链表整表创建的算法思路:
1.声明一指针 p 和计数器变量i;
2.初始化一空链表 L;
3.让 L 的头结点的指针指向 NULL,即建立一个带头结点的单链表;
4.循环:
生成一新结点赋值给 p;
随机生成一数字赋值给 p 的数据域 p->data;
将 p 插入到头结点与前一新结点之间。
算法代码如下:
/* 随机产生 n 个元素的值,建立带表头结点的单链线性表 L(头插法) */
void CreateListHead(LinkList *L, int n)
{
LinkList p;
int i;
/* 初始化随机数种子 */
srand(time(0));
*L = (LinkList)malloc(sizeof(Node));
/* 先建立一个带头结点的单链表 */
(*L)->next = NULL;
for (i = 0; i < n; i++)
{
/* 生成新结点 */
p = (LinkList)malloc(sizeof(Node));
/* 随机生成 100 以内的数字 */
p->data = rand() % 100 + 1;
p->next = (*L)->next;
/* 插入到表头 */
(*L)->next = p;
}
}
这段算法代码里,我们其实用的是插队的办法,就是始终让新结点在第一的位置。我也可以把这种算法简称为头插法,如图:
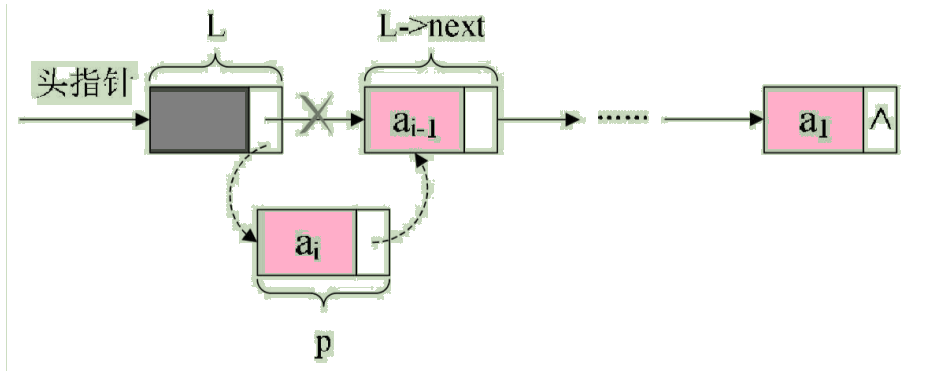
我们还可以采用另一种方式建立一个单链表,先来看实现代码:
/* 随机产生 n 个元素的值,建立带表头结点的单链线性表 L(尾插法) */
void CreateListTail(LinkList *L, int n)
{
LinkList p, r;
int i;
/* 初始化随机数种子 */
srand(time(0));
/* 为整个线性表 */
*L = (LinkList)malloc(sizeof(Node));
/* r 为指向尾部的结点 */
r = *L;
for (i = 0; i < n; i++)
{
/* 生成新结点 */
p = (Node *)malloc(sizeof(Node));
/* 随机生成 100 以内的数字 */
p->data = rand() % 100 + 1;
/* 将表尾终端结点的指针指向新结点 */
r->next = p;
/* 将当前的新结点定义为表尾终端结点 */
r = p;
}
/* 表示当前链表结束 */
r-> = NULL;
}
注意L与r的关系,L是指整个单链表,而r是指向尾结点的变量,r会随着循环不断地变化结点,而L则是随着循环增长为一个多结点的链表。
5.单链表的整表删除
单链表整表删除的算法思路如下:
1.声明一指针p和q;
2.将第一个结点赋值给p;
3.循环:
将下一结点赋值给q;
释放p;
将q赋值给p。
算法实现代码如下:
/* 初始条件:顺序线性表 L 已存在,操作结果:将 L 重置为空表 */
Status ClearList(LinkList *L)
{
LinkList p, q;
/* p 指向第一个结点 */
p = (*L)->next;
/* 没到表尾 */
while (p)
{
q = p->next;
free(p);
p = q;
}
/* 头结点指针域为空 */
(*L)->next = NULL;
return OK;
}
注意:代码中为啥要有一个 q 存在,直接 free§,然后 p = p->next ; 不就行了吗,在这里我们要知道 p 指向一个结点,它除了有数据域,还有指针域。在做 free§ 的时候,是对它整个结点进行删除和内存释放的工作。
6.单链表结构与顺序存储结构优缺点
话不多说,上图:

1.循环链表
将单链表中终端结点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表(circular linked list)。
循环链表可以从任意一个结点出发,访问到链表的全部结点。
为了使空链表与非空链表处理一致,我们通常设一个头结点,当然,这并不是说,循环链表一定要头结点,这需要注意。循环链表带有头结点的空链表如图:
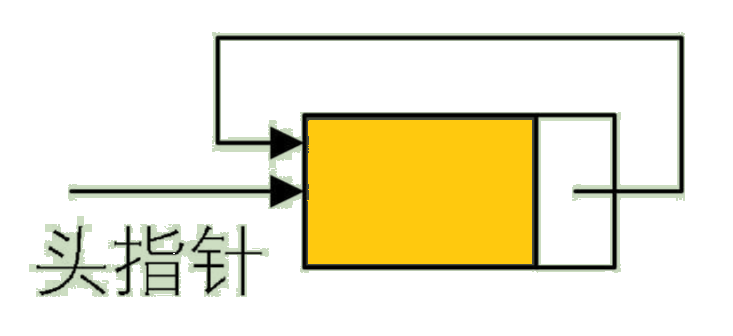
对于非空的循环链表就如图:

循环链表和单链表的主要差异就在于循环的判断条件上,原来是判断 p->next 是否为空,现在则是
p->next 不等于头结点,则循环未结束。
在单链表中,我们有了头结点时,我们可以用O(1)的时间访问第一个结点,但对于要访问到最后一个结点,却需要O(n)时间,因为我们需要将单链表全部扫描一遍。
有没有可能用O(1)的时间由链表指针访问到最后一个结点呢?当然可以。
不过我们需要改造一下这个循环链表,不用头指针,而是用指向终端结点的尾指针来表示循环链表,此时查找开始结点和终端结点都很方便了。如图:

从上图中可以看到,终端结点用尾指针 rear 指示,则查找终端结点是 O(1),而开始结点,其实就是rear->next->next,其时间复杂也为 O(1)。
举个程序的例子,要将两个循环链表合并成一个表时,有了尾指针就非常简单了。比如下面的这两个循环链表,它们的尾指针分别是rearA和rearB,如图:
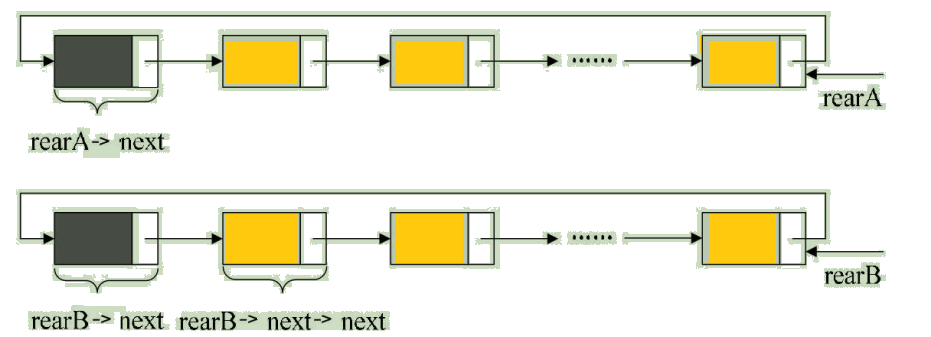
要想把它们合并,只需要如下的操作即可,如图:
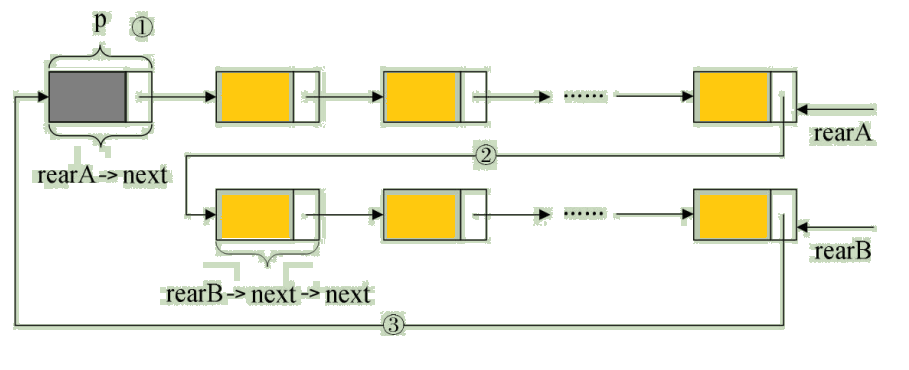
光说不写假把式,代码如下:
/* 保存 A 表的头结点,即 ① */
p = rearA->next;
/* 将本是指向 B 表的第一个结点(不是头结点)赋值给 RearA->next,即 ② */
rearA->next = rearB->next->next;
q = rearB->next;
/* 将原 A 表的头结点赋值给 rearB->next,即 ③ */
rearB->next = p;
/* 释放 q */
free(q);
2.双向链表
我们的单链表,总是从头到尾找结点,难道就不可以正反遍历都可以吗?当然可以,只不过需要加点东西而已。
我们在单链表中,有了next指针,这就使得我们要查找下一结点的时间复杂度为O(1)。可是如果我们要查找的是上一结点的话,那最坏的时间复杂度就是O(n)了,因为我们每次都要从头开始遍历查找。
为了克服单向性这一缺点,我们的老科学家们,设计出了双向链表。双向链表(double linkedlist)是在单链表的每个结点中,再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域,一个指向直接后继,另一个指向直接前驱。
/* 线性表的双向链表存储结构 */
typedef struct DulNode{
ElemType data;
struct DuLNode *prior; /* 直接前驱指针 */
struct DuLNode *next; /* 直接后继指针 */
} DulNode, *DuLinkList;
既然单链表也可以有循环链表,那么双向链表当然也可以是循环表。双向链表的循环带头结点的空链表如图:
非空的循环的带头结点的双向链表如图:
由于这是双向链表,那么对于链表中的某一个结点p,它的 后继的前驱 和 它的 前驱的后继 自然也是它自己,即:
p->next->prior = p = p->prior->next
双向链表是单链表中扩展出来的结构,所以它的很多操作是和单链表相同的,比如求长度的ListLength,查找元素的 GetElem,获得元素位置的 LocateElem 等,这些操作都只要涉及一个方向的指针即可,另一指针多了也不能提供什么帮助。
就像人生一样,想享乐就得先努力,欲收获就得付代价。双向链表既然是比单链表多了如可以反向遍历查找等数据结构,那么也就需要付出一些小的代价:在插入和删除时,需要更改两个指针变量。
插入操作时,其实并不复杂,不过顺序很重要,千万不能写反了。
我们现在假设存储元素e的结点为s,要实现将结点s插入到结点p和p->next之间需要下面几步,如图:
步骤如下:
/* 把 p 赋值给 s 的前驱,如图中 ① */
s->prior = p;
/* 把p->next赋值给s的后继,如图中 ② */
s->next = p->next;
/* 把s赋值给p->next的前驱,如图中③ */
p->next->prior = s;
/* 把s赋值给p的后继,如图中④ */
p->next = s;
关键在于它们的顺序,由于第2步和第3步都用到了p->next。如果第4步先执行,则会使得p->next提前变成了s,使得插入的工作完不成。所以我们不妨把上面这张图在理解的基础上记忆,顺序是先搞定s的前驱和后继,再搞定后结点的前驱,最后解决前结点的后继。
如果插入操作理解了,那么删除操作,就比较简单了。
若要删除结点p,只需要下面两步骤,如图:
步骤如下:
/* 把p->next赋值给p->prior的后继,如图中① */
p->prior->next = p->next;
/* 把p->prior赋值给p->next的前驱,如图中② */
p->next->prior = p->prior;
/* 释放结点 */
free(p);
双向链表相对于单链表来说,要更复杂一些,毕竟它多了prior指针,对于插入和删除时,需要格外小心。另外它由于每个结点都需要记录两份指针,所以在空间上是要占用略多一些的。不过,由于它良好的对称性,使得对某个结点的前后结点的操作,带来了方便,可以有效提高算法的时间性能。说白了,就是用空间来换时间。
3.静态链表
C语言具有指针这一强大的功能,也是众多计算机领域的人用来描述数据结构首选C语言的原因之一。指针可以使C非常容易的操作内存中的地址和数据,这比其他高级语言更加灵活方便。Java、C#等面向对象语言,虽然不使用指针,但因为启用了对象引用机制,从某种角度也间接实现了指针的某些作用。但对于其他一些语言,如Basic、Fortran等早期的编程语言对于一些数据结构的操作就没有那么方便了。
有前辈想出来用数组来代替指针,描述单链表:首先让数组的元素都是由两个数据域组成,data和cur。也就是说,数组的每个下标都对应一个data和一个cur。数据域data,用来存放数据元素,也就是通常我们要处理的数据;而cur相当于单链表中的next指针,存放该元素的后继在数组中的下标,我们把cur叫做游标。
我们把这种用数组描述的链表叫做静态链表,这种描述方法还有起名叫做游标实现法。
为了我们方便插入数据,通常会把数组建立得大一些,以便有一些空闲空间可以便于插入时不至于溢出。
用代码描述一下:
/* 线性表的静态链表存储结构 */
/* 假设链表的最大长度是1000 */
#define MAXSIZE 1000
typedef struct
{
ElemType data;
/* 游标(Cursor),为0时表示无指向 */
int cur;
} Component,
StaticLinkList[MAXSIZE];
对数组第一个和最后一个元素作为特殊元素处理,不存数据。我们通常把未被使用的数组元素称为备用链表。而数组第一个元素,即下标为0的元素的cur就存放备用链表的第一个结点的下标;而数组的最后一个元素的cur则存放第一个有数值的元素的下标,相当于单链表中的头结点作用,当整个链表为空时,则为0。如图:
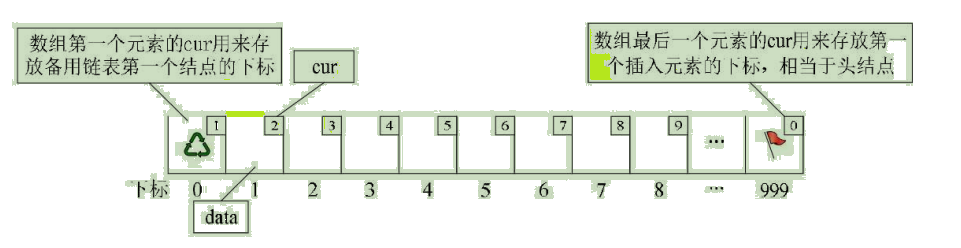
假设我们已经将数据存入静态链表,比如分别存放着“甲”、“乙”、“丁”、“戊”、“己”、“庚”等数据,则它的状态如图所示: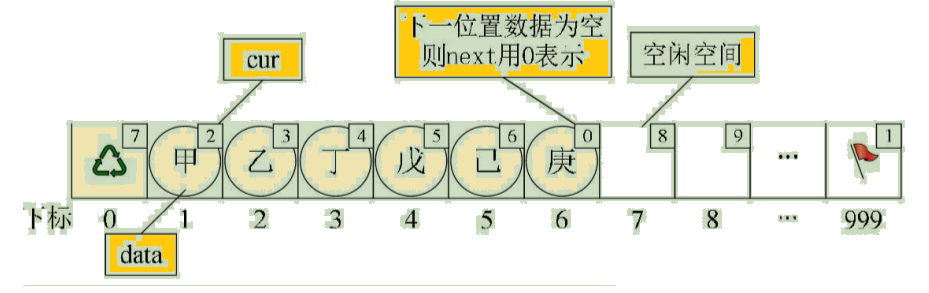
此时“甲”这里就存有下一元素“乙”的游标2,“乙”则存有下一元素“丁”的下标3。而“庚”是最后一个有值元素,所以它的cur设置为0。而最后一个元素的cur则因“甲”是第一有值元素而存有它的下标为1。而第一个元素则因空闲空间的第一个元素下标为7,所以它的cur存有7。
(1)静态链表的插入操作
静态链表中解决的是:如何用静态模拟动态链表结构的存储空间的分配,需要时申请,无用时释放。
在动态链表中,结点的申请和释放分别借用 malloc() 和 free() 两个函数实现。在静态链表中,操作的是数组,不存在像动态链表的结点申请和释放问题,所以我们需要自己实现这两个函数,才可以做插入和删除操作。
为了辨明数组中哪些分量未被使用,解决办法是将所有未被使用过的及被删除的分量用游标链成一个备用的链表,每当进行插入时,便可以从备用链表上取的第一个结点作为待插入的新结点。
/* 若备用空间链表非空,则返回分配的结点下标,否则返回 0 */
int Malloc_SLL(StaticLinkList space)
{
/* 当前数组第一个元素的 cur 存的值,就是要返回的第一个备用的空闲的下标 */
int i = space[0].cur;
/* 由于要拿出一个分量来使用了,所以我们就得把它的下一个分量用来做备用 */
if (space[0].cur)
space[0].cur = space[i].cur;
return i;
}
这段代码,一方面它的作用就是返回一个下标值,这个值就是数组头元素的cur存的第一个空闲的下标。从上面的图示例子来看,其实就是返回7。
那么既然下标为7的分量准备要使用了,就得有接替者,所以就把分量7的cur值赋值给头元素,也就是把8给space[0].cur,之后就可以继续分配新的空闲分量,实现类似malloc()函数的作用。
现在我们如果需要在“乙”和“丁”之间,插入一个值为“丙”的元素,按照以前顺序存储结构的做法,应该要把“丁”、“戊”、“己”、“庚”这些元素都往后移一位。但目前不需要,因为我们有了新的手段。
新元素“丙”,想插队是吧?可以,你先悄悄地在队伍最后一排第7个游标位置待着,我一会就能帮你搞定。我接着找到了“乙”,告诉他,你的cur不是游标为3的“丁”了,这点小钱,意思意思,你把你的下一位的游标改为7就可以了。“乙”叹了口气,收了钱把cur值改了。此时再回到“丙”那里,说你把你的cur改为3。就这样,在绝大多数人都不知道的情况下,整个排队的次序发生了改变。如图:
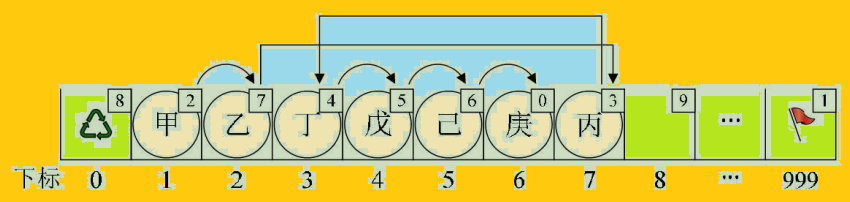
上图实现代码如下:
/* 在 L 中第 i 个元素之前插入新的数据元素 e */
Status ListInsert(StaticLinkList L, int i, ElemType e)
{
int j, k, l;
/* 注意 k 首先是最后一个元素的下标 */
k = MAX_SIZE - 1;
if (i < 1 || i > ListLength(L) + 1)
return ERROR;
/* 获得空闲分量的下标 */
j = Malloc_SLL(L);
if (j)
{
/* 将数据赋值给此分量的data */
L[j].data = e;
/* 找到第i个元素之前的位置 */
for (l = 1; l <= i - 1; l++)
k = L[k].cur;
/* 把第i个元素之前的cur赋值给新元素的cur */
L[j].cur = L[k].cur;
/* 把新元素的下标赋值给第i个元素之前元素的cur */
L[k].cur = j;
return OK;
}
return ERROR;
}
当我们执行插入语句时,我们的目的是要在“乙”和“丁”之间插入“丙”。调用代码时,输入 i 值为 3。
让 k = MAX_SIZE-1=999。
j = Malloc_SSL(L) = 7。此时下标为 0 的 cur 也因为 7 要被占用而更改备用链表的值为 8。
for 循环 l 由 1 到 2,执行两次。代码 k = L[k].cur ; 使得 k = 999,得到 k = L[999].cur = 1,再得到 k = L[1].cur = 2。
L[j].cur = L[k].cur ; 因 j = 7,而 k = 2 得到L[7].cur=L[2].cur = 3。这就是刚才我说的让“丙”把它的cur 改为 3的意思。
L[k].cur = j;意思就是L[2].cur = 7。也就是让“乙”得点好处,把它的 cur 改为指向“丙”的下标 7。
就这样,我们实现了在数组中,实现不移动元素,插入了数据的操作。
(2)静态链表的删除操作
删除元素时,原来是需要释放结点的函数 free()。现在我们要自己实现它:
/* 删除在 L 中第 i 个元素 e */
Status ListDelete(StaticLinkList L, int i)
{
int j, k;
if (i < 1 || i > ListLength(L))
return ERROR;
k = MAX_SIZE - 1;
for (j = 1; j <= i; j++)
k = L[k].cur;
j = L[k].cur;
L[k].cur = L[i].cur;
Free_SSL(L,j); /* 看下文 */
return OK;
}
将下标为k的空闲结点回收到备用链表代码:
/* 将下标为k的空闲结点回收到备用链表 */
void Free_SSL(StaticLinkList space, int k)
{
/* 把第一个元素 cur 值赋给要删除的分量 cur */
space[k].cur = space[0].cur;
/* 把要删除的分量下标赋值给第一个元素的 cur */
space[0].cur = k;
}
甲现在要走,这个位置就空出来了,也就是,未来如果有新人来,最优先考虑这里,所以原来的第一个空位分量,即下标是 8 的分量,它降级了,把 8 给“甲”所在下标为 1 的分量的 cur,也就是 space[1].cur = space[0].cur = 8,而 space[0].cur = k = 1 其实就是让这个删除的位置成为第一个优先空位,把它存入第一个元素的 cur 中,如图:

(3)静态链表的优缺点
上图:
- 点赞
- 收藏
- 关注作者


评论(0)