前言

根据上一章我们所介绍的单钥密码体制也就是对称密码体制分为流密码与分组密码，本章我们来学习流密码。

2.1 流密码的基本概念

Q:什么是密钥流？
A:随机产生的一串随机数，由于人为随机可能会出现规律所以我们将使用寄存器来产生密钥
流密码的核心：密钥
在流密码中，加密方法可以公开，但密钥需要进行保密（有点像双钥密码体制，但只有一个密钥）
密码学中计算大多用到加法、乘法和异或，减法用加负数代替，除法用逆元代替。
下图是分组密码和流密码的比较，二者区别在于有无记忆性：
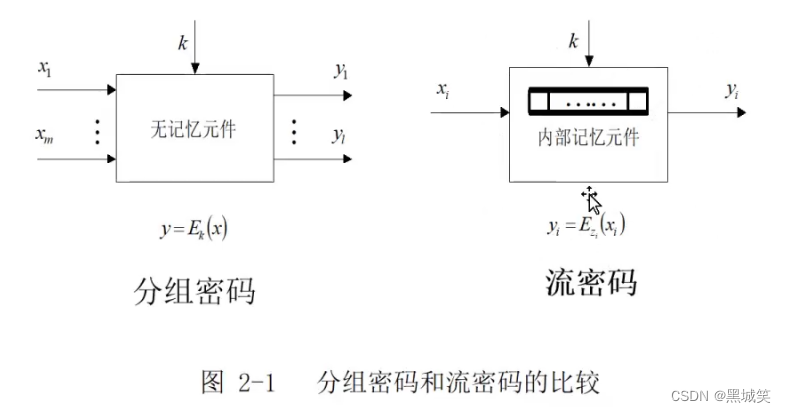上图内部记忆元件一般指寄存器

2.1.1 同步流密码

同步流密码与明文字符无关，密文字符不依赖于明文字符。可将同步流密码的加密器分为密钥流产生器和加密变换器，如果加密变换与解密变换互为可逆，由此产生下图同步流密码体制模型。
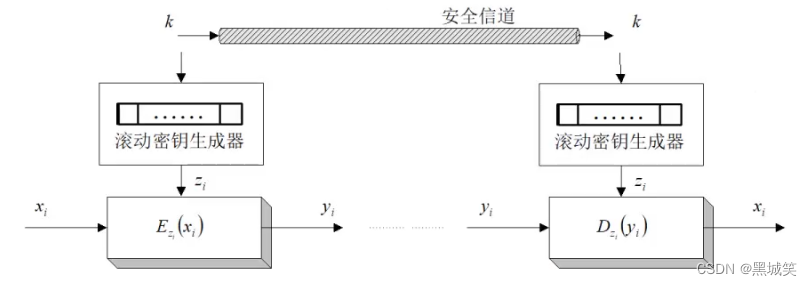密钥流产生器产生密钥后由加密变换器将密钥流进行处理（z是密钥流，在上图和本次学习暂忽略使用加密变换器的情况），上图k是密钥流的第一个数，同步流密码只需传递一个数k，因为有同样的滚动密钥生成器，所以只由密钥流的第一个数可推出整个密钥流。
在同步流密码中一般使用异或加密。

2.1.2 密钥流产生器

密钥生成器最初设计为限状态自动机，有限状态自动机是具有离散有限输入和输出的数学模型，它由三部分组成：
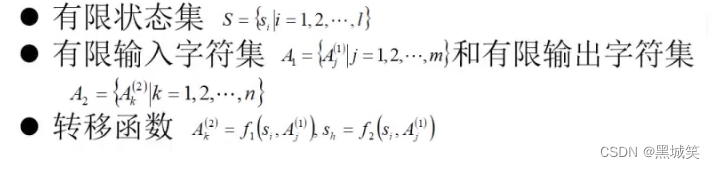它是一种伪随机所以状态是有限的，输入和输出是有限的，函数（规则）是有规律的，所以是有限状态自动机。

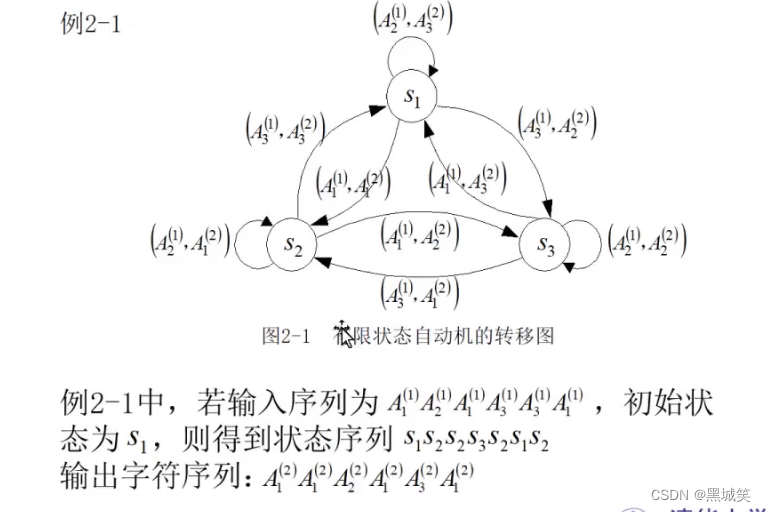
• 初始状态S~1~输入A~1~^(1)^，寻找S~1~此刻前往它下一状态的途中经过哪条含有A~1~^(1)^的规律，由此得到输出状态。

  查看图片后，我们不难发现有条路径为（A~1~^(1)^，A~1~^(2)^），经过这条路径后，我们将输出字符A~1~^(2)^并且将状态从S~1~转到了S~2~

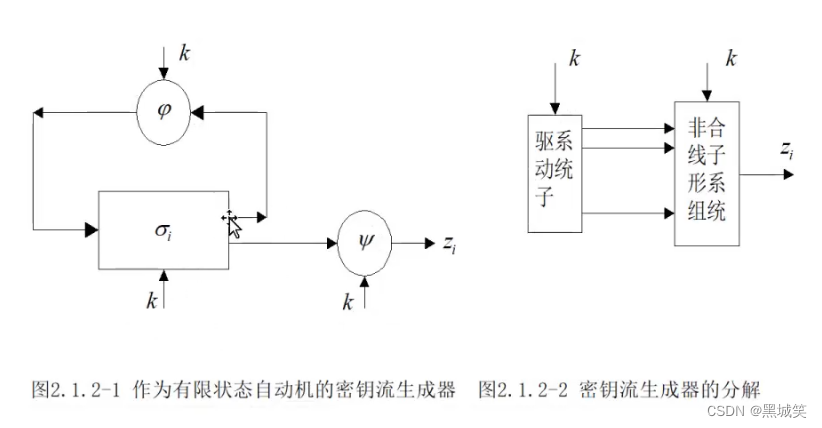首先需要一个初始状态σ~0~，经过i次函数φ进行规律运算后它的状态变为σ~i~，得到i个输出z~i~
图2.1.2-1的左半块为驱动子系统，右半块为非线性组合子系统，如上图2.1.2-2所示

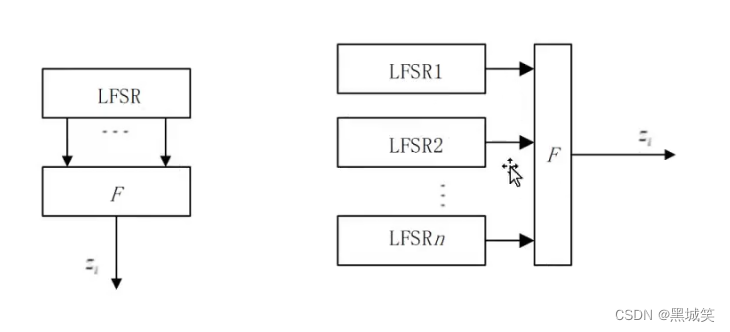
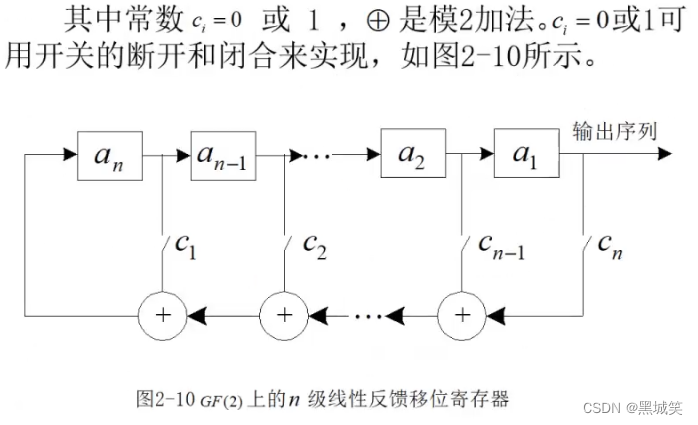
由于使用有限状态自动机不够完善，所以现在最常见的密钥流产生器其实是，线性移位寄存器，下图是目前常见的密钥流产生器，由一个或多个线性移位寄存器（LFSR）组成：

2.2 线性反馈移位寄存器

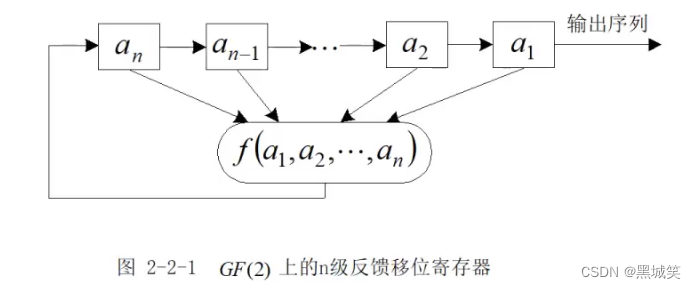
线性反馈移位寄存器产生的数字是非线性的，但它的f呈现的是线性的关系，这里的a都有n个状态，是n级移位寄存器

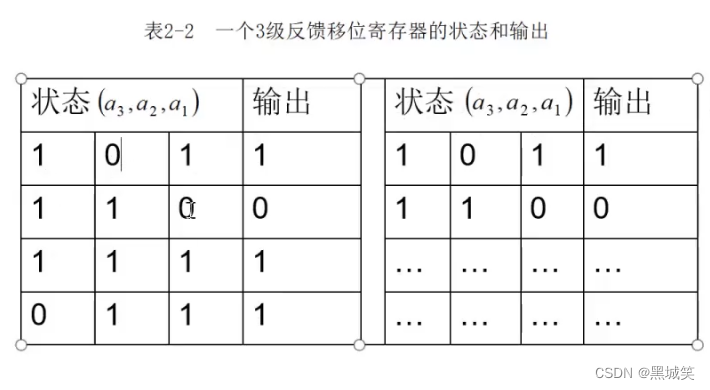
下图是一个例子：
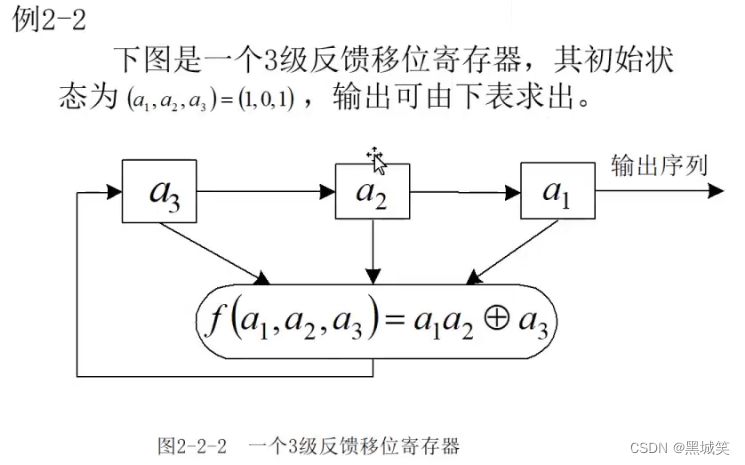3级移位寄存器有3种状态。
第一步：f(1,0,1)=10⊕1=1，将a1=1推出，剩下向前挪一位，令a₃=1
第二部：f(0,1,1)=01⊕1=1，将a1=0推出，剩下向前挪一位，令a₃=1
第三步：f(1,1,1)=1*1⊕1=0，将a1=1推出，剩下向前挪一位，令a₃=0
……


线性移位寄存器的最大周期为2^n^-1

2.3 线性移位寄存器的一元多形式表示

其周期为2^n^-1

2.4m序列的伪随机性

密钥流的安全性决定了流密码的安全性，要求密钥流具有随机性
a是一串随机序列，如00110111，两个数字挨在一起则为2游程，3个则为3流程，所以这串数字是0的2 游程，1的2游程，0的1游程，1的3游程

2.5 m序列的破译

由线性反馈移位寄存器组成的密钥生成器是目前最常用的流密码体制，其产生密钥是m序列。m序列的破译是破译c是什么，即破解线性移位寄存器
已知2n长的明密文对，可知它的密钥，密钥是明文和密文的异或

由一小段密钥可破解线性移位寄存器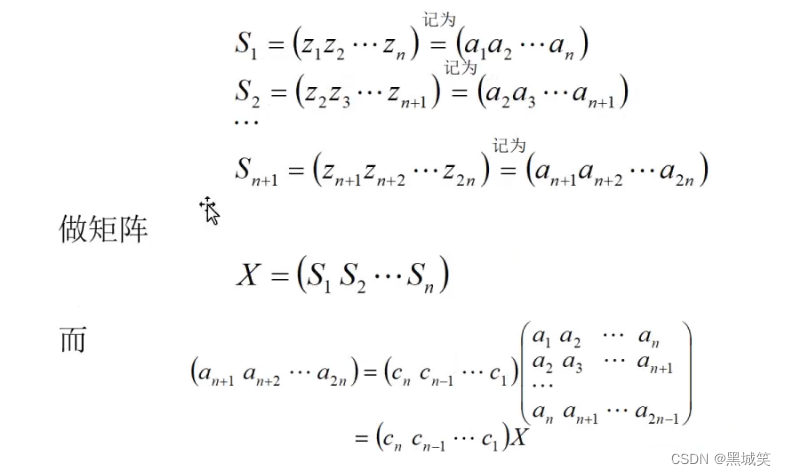

2.6 非线性序列（了解）

好了，以上就是密码学第二章的全部内容啦，感谢大家的观看，求点赞求收藏求评论
欢迎大家关注我的账号：黑城笑
更多技术分享等待大家