【路径规划】基于matlab蚁群算法机器人大规模栅格地图最短路径规划【含Matlab源码 1860期】
一、蚁群算法及栅格地图简介
随着机器人技术在诸多领域的应用, 如机器人协作焊接、灾后搜救、军事、太空探索、深海勘探、家用和服务行业等, 机器人的发展正向智能化方向延伸, 要求其具有自组织、自学习、自适应等能力.机器人路径规划是指机器人从初始位置按某种法则避开障碍物、无碰撞地到达目标位置.目前国内外对路径规划的研究应用较多的方法主要有:人工势场法、概率路径图法[3]、可视图法、栅格法、神经网络算法、遗传算法、粒子群算法、蚁群算法.
栅格法是将机器人的搜索空间分解成若干个规格相等单元, 将复杂的环境问题分解成简单问题, 适用于静态环境的路径规划, 且算法计算量小, 便于实现, 但在复杂的环境中, 易使规划时间延长, 系统的实时性不够.蚁群算法是一种新型的仿生算法, 以蚂蚁觅食为模型, 通过前代蚂蚁在走过的路径上遗留信息素的强弱选择路径.该算法有较好的正反馈性、并行性及鲁棒性;但当遇到复杂问题时, 会导致搜索时间长、陷入局部最优、停滞和死锁等情况.因此, 结合栅格法和蚁群算法的优缺点, 将栅格法与蚁群算法相结合进行路径规划, 先建立栅格地图, 再利用蚁群算法进行全局搜索, 可提高算法性能.
1 栅格模型建立
1.1 栅格法应用于路径规划的简介
栅格法是由W.E.Howden于1968年提出, 主要是根据环境建立一个路径栅格地图 (map) .基本原理是将机器人工作环境分割成无数细小的具有二值信息的网格单元, 每个网格的规格由机器人的步长决定, 即一个步长代表一个网格大小.在进行网格划分时, 无论是障碍物栅格还是非障碍物栅格不满一个时, 将其填满, 按一个栅格计算.
环境信息由黑白网格表示.黑色网格代表障碍物 (barrier) , 表示不可行区域;白色网格代表可通行区域, 又称自由区域.栅格法将不可行区域和自由区域用一个二进制矩阵表示, 矩阵中1代表障碍物, 0代表自由栅格, 由此在环境中建立一个可描述环境的路径规划地图.
1.2 栅格地图的建立
假设SP为机器人在二维空间中的一个规则的凸多边形运动场地, 将场地分解成M×N个栅格, 由自由栅格和障碍物栅格组成, 其运动方式主要为八叉树型形式.自由栅格的集合P={P1, P2, …, Pm}, 障碍物栅格的集合B={B1, B2, …, Bn}, 设A为机器人工作场地的栅格集合, 其表达式为A=P∪B.
本文根据实验场地建立一个10×10栅格地图, 如图1所示.图中栅格的序号集合C={1, 2, 3, …, 100}.假设1号位为初始位置Gstart, 100号位为目标位置Ggoal, 机器人从初始位置通过n次迭代搜索找到最优路径, 其中初始位置Gstart∈A且, 目标位置Ggoal∈A且, 规定初始位置与目标位置不重合, 在进行路径搜索时主要以八叉树型形式搜索.
2 蚁群算法的路径规划问题描述
2.1 基本蚁群算法的描述
蚁群算法是一种模仿蚁群觅食的仿生学算法, 其基本原理是将每台机器人看作蚂蚁群体中的一只蚂蚁.蚂蚁在进行路径搜索时通过蚁群在路径上遗留的信息素强度, 向其它蚂蚁传递信息, 实现机器人之间的信息交换.通常情况下路径是未知的, 蚂蚁在选择路径时一般根据概率Pkij (t) 随机选择.
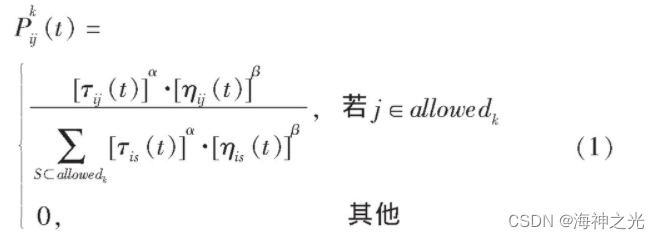
其中:α为启发式因子;β是期望启发式因子;τij为机器人k从位置i到位置j这段路径上所留信息素强度;allowedk表示机器人未访问过的栅格的集合;ηij (t) 为启发式函数, 启发式函数的大小与i、j之间的距离有关, dij值越小, i, j之间的关系越亲密, 反之则疏远, 其表达式为
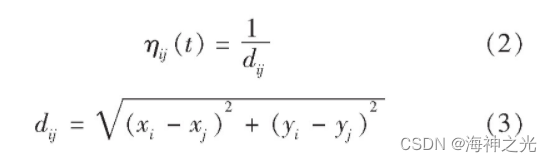
式中 (xi, yi) 为点的位置坐标, (xj, yj) 为点的位置坐标.
2.2 蚂蚁信息素更新
机器人在路径搜索的过程中会在路径上留下新的信息素, 随着时间推移留在路径上的信息素强度不断增加, 为避免在搜索路径上残留的信息素过多而淹没启发式信息, 因此, 当蚂蚁完成一次搜索时, 对所有路径上的信息素进行一次更新, 其表达式为
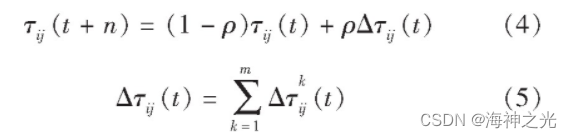
其中:1-ρ表示信息素残留因子, ρ表示信息素挥发系数;Δτij (t) 表示蚂蚁在本次循环中路径 (i, j) 上的信息素增量, Δτkij (t) 表示第k只蚂蚁经过路径 (i, j) 时在本次循环中的信息素增加量.根据信息素规则, 选择蚁周 (ant-cycle) 模型作为蚂蚁信息素更新模型.

式中, Q表示信息素强度, Lk表示第k只蚂蚁在本次循环中所有路径的总长度.
二、部分源代码
clear;clc;
tic;
%% 障碍物导入,如果起点终点设置不好,会出现错误
% load('barrier_1200x1200.mat'); goal = 1240000; start = 1;
load('barrier_reality_320.mat'); goal = 102079; start = 1;
graph = barrier;
%% 参数的设置
antNumber = 30; % 蚂蚁数目
NCmax = 200; % 最大迭代次数
rhoGlobal = 0.08; % 全局信息素挥发系数
rhoLocal = 0.1; % 局部信息素挥发系数
Beta = 1; % 启发函数式因子
Alpha = 1; % 信息素函数因子
q0 = 0.8; % 偏向选择的阈值
X = size(graph,1); % 问题的状态空间矩阵的行数
Y = size(graph,2); % 问题的状态空间矩阵的列数
tauInit = 1/((X+Y)*(X*Y));% 初始化信息素的量
tauInfo = tauInfoInit(X,Y,tauInit);
upPheromone = 500; % 信息素上限
lowPheromone = tauInit; % 信息素下限
bestSoFar_path_length = inf; % 当前最优路径长度
bestSoFar_pathNode = [];
bestSoFar_PathNode = cell(1,NCmax);
bestSoFar_PathLength = zeros(1,NCmax);
%%
for NC=1:NCmax
for k=1:antNumber
currentNode = start;
pathInfo = currentNode; % 记录一只蚂蚁的行驶路径的节点信息
path_length = 0; % 记录蚂蚁走过的路径长度
availableNode = findNextNodeSet(graph,currentNode); %% 未经过禁忌表处理的可选节点
nodeNumber = size(availableNode,1);
while(nodeNumber>0&¤tNode~=goal)
heuristicInfo = computeHeuristicInfo(goal,currentNode,graph);
tauInfo_ = tauInfo(currentNode,:)';
[info,availableNode_] = computeConvertProbability(...
tauInfo_,heuristicInfo,pathInfo,availableNode,Alpha,Beta); % 经过禁忌表处理的可选节点
nodeNumber = size(availableNode_,1);
if nodeNumber==0
break
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
三、运行结果
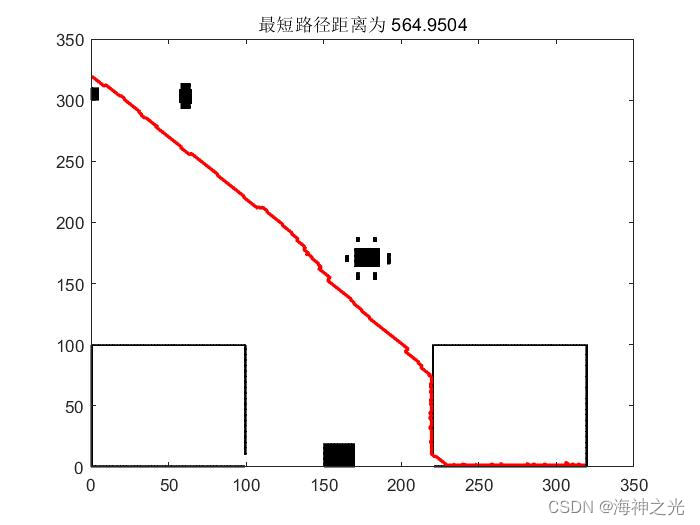
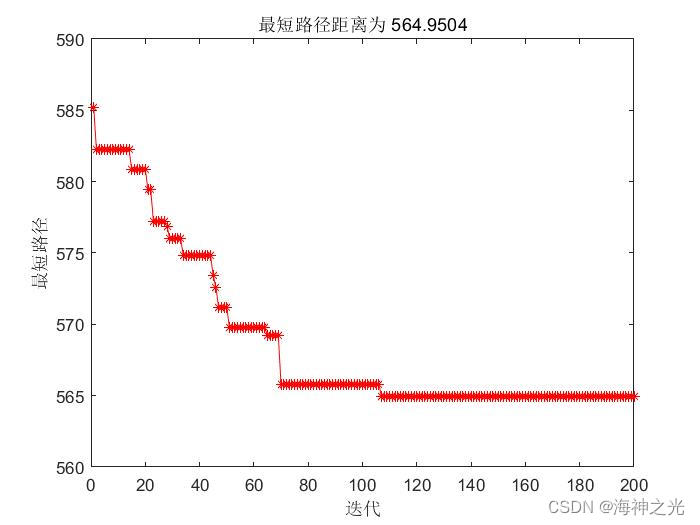
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]周东健,张兴国,马海波,李成浩,郭旭.基于栅格地图-蚁群算法的机器人最优路径规划[J].南通大学学报(自然科学版). 2013,12(04)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/125054508
- 点赞
- 收藏
- 关注作者


评论(0)