⭐️前面的话⭐️

本篇文章带大家认识数据结构——堆，所谓的堆，其实就是使用顺序表实现的树，前面所介绍的二叉树是基于链式结构所实现的，本文将介绍底层为顺序表的二叉树，由于使用顺序表实现非完全二叉树会存在内存空间浪费问题，所以常常使用顺序表实现完全二叉树，而这个使用顺序表所实现的完全二叉树就是堆。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创！
📆华为云首发时间：🌴2022年5月31日🌴
✉️坚持和努力一定能换来诗与远方！
💭参考书籍：📚《Java核心技术卷1》，📚《数据结构》，📚《Java编程思想》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

---

题外话：在正式开始之前，我们先来看一看集合框架，画上√的表示博主已经介绍完毕了，可以翻看JavaSE系列专栏进行寻找，画上⭐️表示本文所介绍的内容。

---

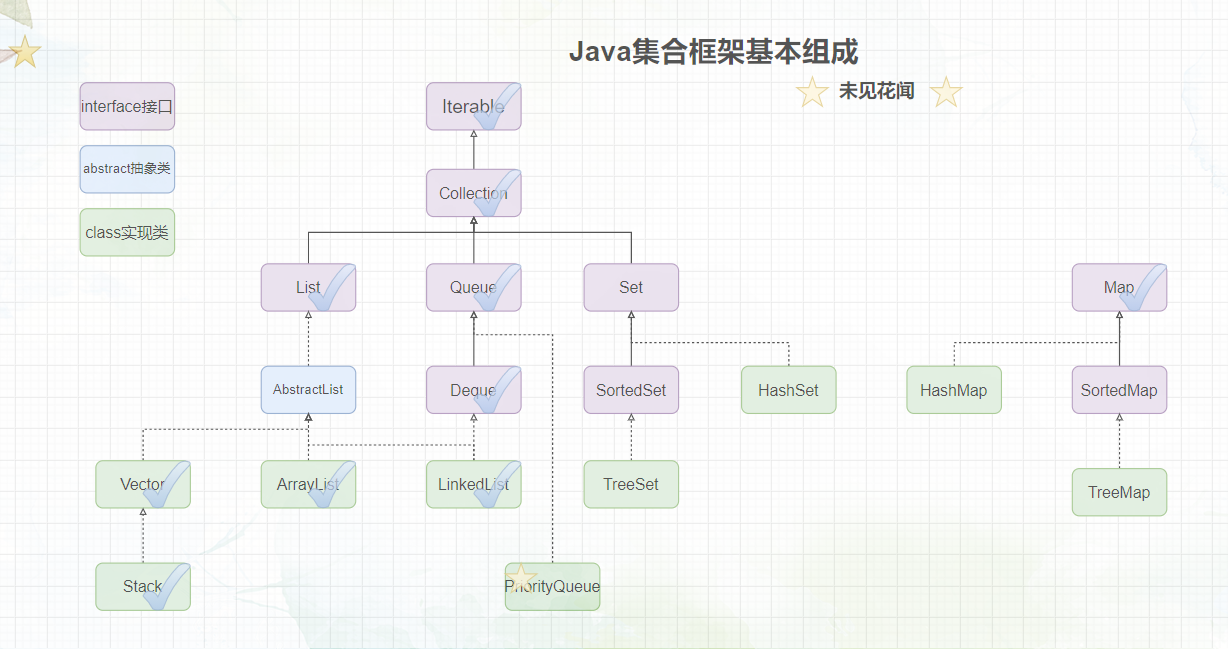
1.堆

1.1什么是堆？

所谓堆，就是使用顺序表实现的完全二叉树 ，堆中的根结点的值大于所有非空子树结点的值，则该堆被称为大堆（大根堆），反之，堆中的根结点的值小于所有非空子树结点的值，则该堆被称为小堆（小根堆）。

例如下面这一个数组：

该数组对应的堆为：

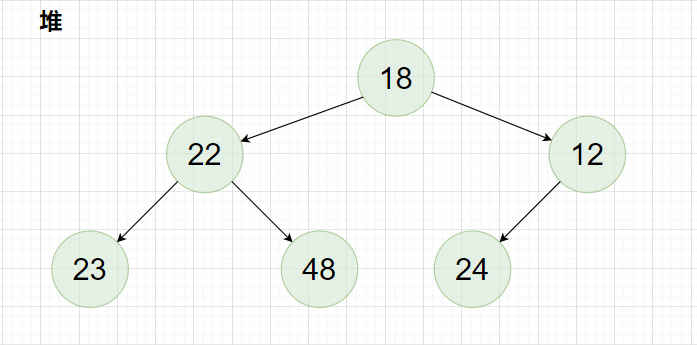
大根堆：

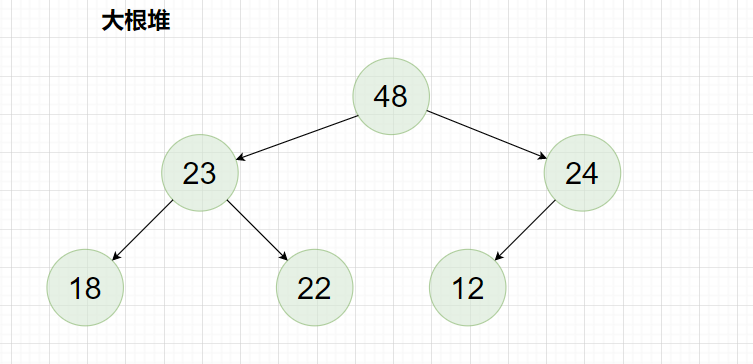
小根堆：

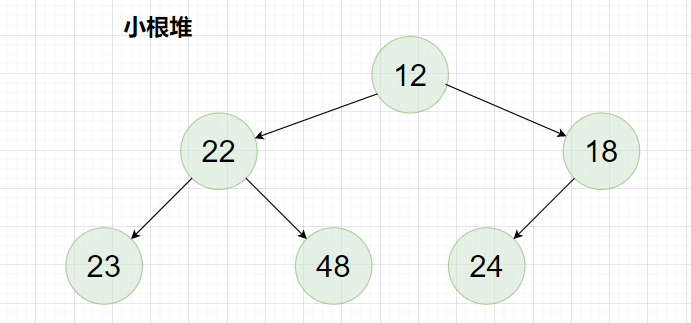
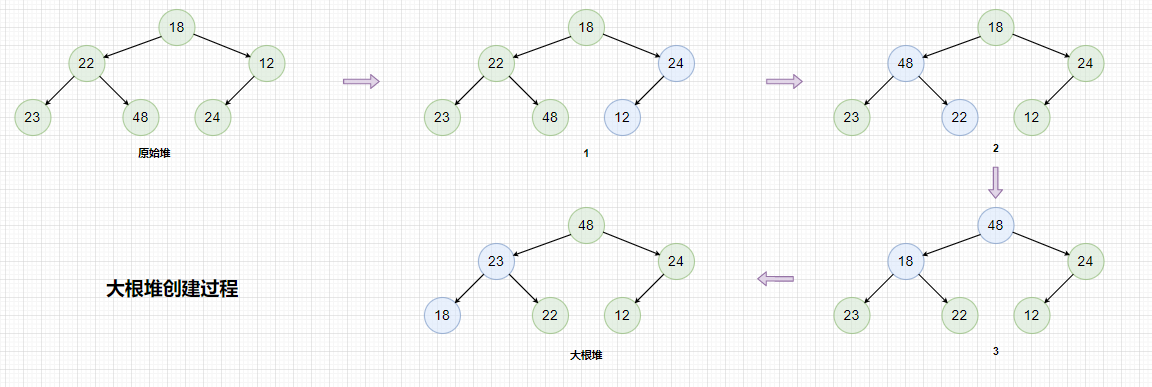
1.2堆的创建

我们知道堆是由顺序表实现的，并且堆顶的元素大小大于（或小于）子堆的元素大小，堆的本质就是一棵完全二叉树，所以可以根据这个特点总结出堆是如何创建的。

1. 找到堆中最后一个子树，该子树根结点不能为叶子结点。
2. 对该子树进行向下方向的调整，若该堆为大根堆，找到该树两个子结点值较大的结点与根结点进行比较，如果这个子结点比根结点要大，则先交换两结点的值，然后在堆的大小范围内，对被交换结点的子树作相同的调整，直到被调整的子树下标超出堆的大小或满足大堆条件，反之如果堆为小根堆，找到该树两个子结点值较小的结点与根结点进行比较，如果这个子结点比根结点要小，则先交换两结点的值，然后在堆的大小范围内，对被交换结点的子树作相同的调整，直到被调整的子树下标超出堆的大小或满足小堆条件。
3. 从最后一棵子树（该树不为叶子，最右边一棵高度为2的子树）开始，整棵树（以堆顶结点所代表的树）为结束，按此顺序对所有树进行向下调整，这个大（小）堆就创建好了。

不妨设最后一棵子树（非叶子）所对应数组下标为parent，其左子树根结点为child，堆大小为len，由于该树是一棵完全二叉树，所以下标会满足 $child=2*parent+1；parent=(child-1)/2$
最后一个结点下标为 $len-1$，父结点下标为 $(len-2)/2$。

对于向下调整中，以创建大根堆为例，如果一棵子树右结点存在且大于左结点的值，则child++指向右结点。

堆的结构：

public class Heap {
    private int[] elem;
    private int usedSize;
    public Heap() {
        this.elem = new int[10];
    }
    //基本操作方法
}

代码实现（Java）：创建大根堆为例

	/**
     *
     * @param arr 目标交换数组对象
     * @param index1 下标1
     * @param index2 下标2
     */
    private void swap(int arr[], int index1, int index2) {
        int tmp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = tmp;
    }

/**
     * 向下调整
     * @param parent 父节点下标
     * @param len 堆大小
     */
    public void shiftDown(int parent, int len) {
        int child = 2 * parent + 1;
        while (child < len) {
            if (child + 1 < len && this.elem[child] < this.elem[child + 1]) {
                child++;
            }
            if (this.elem[child] > this.elem[parent]) {
                swap(this.elem, child, parent);
                parent = child;
                child = 2 * parent + 1;
            } else {
                break;
            }
        }
    }

    /**
     * 创建大根堆
     * @param data 堆中的数据
     */
    public void creatCopyBigHeap(int[] data) {
        //拷贝数据
        for (int i = 0; i < data.length; i++) {
            if (isFull()) {
                this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);
            }
            this.elem[i] = data[i];
            usedSize++;
        }
        //从最后一棵完全二叉树子树开始调整
        int child = this.usedSize - 1;
        int parent = (child - 1) / 2;

        while (parent >= 0) {
            shiftDown(parent, usedSize);
            parent--;
        }

    }
//或者直接利用数组对象，不对它进行深拷贝
    public void creatBigHeap(int[] data) {
        //拷贝数据
        this.elem = data;
        usedSize = data.length;
        //从最后一棵完全二叉树子树开始调整
        int child = this.usedSize - 1;
        int parent = (child - 1) / 2;

        while (parent >= 0) {
            shiftDown(parent, usedSize);
            parent--;
        }
    }

建堆的时间复杂度为多少？

建堆的过程是自下而上的，堆的本质就是一棵完全二叉树，不妨设该二叉树的高度为h，堆元素个数为n，建堆时需要对所有高度大于1的子树进行调整，最坏情况下该堆是一个满堆，设该堆所处层次为x（从1开始），则第x层次的子树需要调整h-x次，有 $2^{h-1}$个结点，由于只调整高度大于1的子树，因此x的范围为 $[1,h-1]$。
设调整的次数为 $S$:
（1）$$S=2^{0}(h-1)+2^{1}(h-2)+…+2^{x-1}*(h-x)+…+2^{h-2}*1$$
由上述式子得特点可知S是通项公式为 $等比数列*等差数列$的前n-1项和，对于该形式的通项公式和可以采用错位相减法，第一步乘以公比2：
（2）

$$2S=2^{1}*(h-1)+2^{2}*(h-2)+...+2^{x}*(h-x)+...+2^{h-1}*1$$

（2）-（1）得:

$$S=2^{1}+2^{2}+...+...+2^{h-2}+2^{h-1}-2^{0}*(h-1)$$

我们发现S为等比数列和减去h-1，等比数列求和公式为 $S_n=a_1(1-q^n)/(1-q)$。

$$S=2*(1-2^{h-1})/(-1)-h+1$$

$$S=2^h-h-1$$

完全二叉树中 $h=log_2(n+1)$

$$S=n+1-log_2(n+1)-1=n-log_2(n+1)$$

综上所述，建堆的时间复杂度为O(N)。

2.优先队列PriorityQueue

2.1优先队列

在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 (first in, largest out)的行为特征，通常采用堆数据结构来实现。
比如说一个优先队列是由小根堆实现的，则该队列优先最小的元素出队，反之，优先队列由大根堆实现，则该队列优先最大的元素出队。

2.2PriorityQueue

在java中，PriorityQueue类就是优先队列，默认由小根堆实现，如果想要改变使用大根堆实现，则需要传入对象的比较器，或比较器内部类或lambda表达式所实现的比较器。

PriorityQueue构造方法：

方法	类型	作用
public PriorityQueue()	构造方法	创建一个默认大小的优先队列（java8默认大小为11）
public PriorityQueue(int initialCapacity)	构造方法	指定容量创建优先队列
public PriorityQueue(Comparator<? super E> comparator)	构造方法	指定比较器创建一个默认大小的优先队列
public PriorityQueue(int initialCapacity, Comparator<? super E> comparator)	构造方法	指定比较器指定容量创建优先队列
public PriorityQueue(Collection<? extends E> c)	构造方法	根据集合对象创建优先队列
public PriorityQueue(PriorityQueue<? extends E> c)	构造方法	根据优先队列对象构造优先队列
public PriorityQueue(SortedSet<? extends E> c	构造方法	根据SortedSet对象构造优先队列

import java.util.Comparator;
import java.util.PriorityQueue;

public class Test {
    public static void main(String[] args) {
        PriorityQueue<Integer> priorityQueue1 = new PriorityQueue<>();//创建基于小根堆的优先队列
        priorityQueue1.offer(1);
        priorityQueue1.offer(2);
        priorityQueue1.offer(3);
        System.out.println(priorityQueue1);
        System.out.println("============");
        PriorityQueue<Integer> priorityQueue2 = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1 - o2;
            }
        });//使用隐藏内部类创建基于小根堆的优先队列
        priorityQueue2.offer(1);
        priorityQueue2.offer(2);
        priorityQueue2.offer(3);
        System.out.println(priorityQueue2);
        System.out.println("============");
        PriorityQueue<Integer> priorityQueue3 = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });//使用隐藏内部类创建基于大根堆的优先队列
        priorityQueue3.offer(1);
        priorityQueue3.offer(2);
        priorityQueue3.offer(3);
        System.out.println(priorityQueue3);
        System.out.println("============");
        PriorityQueue<Integer> priorityQueue4 = new PriorityQueue<>((x, y) -> x-y);//使用lambda表达式创建基于小根堆的优先队列
        priorityQueue4.offer(1);
        priorityQueue4.offer(2);
        priorityQueue4.offer(3);
        System.out.println(priorityQueue4);
        System.out.println("============");
        PriorityQueue<Integer> priorityQueue5 = new PriorityQueue<>((x, y) -> y-x);//使用lambda表达式创建基于大根堆的优先队列
        priorityQueue5.offer(1);
        priorityQueue5.offer(2);
        priorityQueue5.offer(3);
        System.out.println(priorityQueue5);
        System.out.println("============");
    }
}

上面的内部类与lambda先知道这么写，后续博文会介绍内部类与lambda表达式。

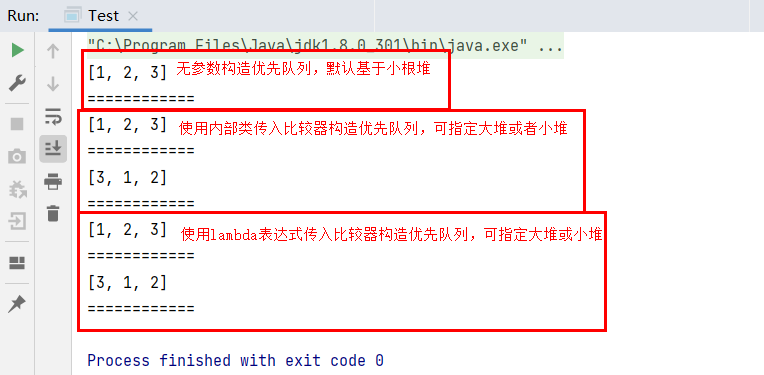
PriorityQueue基本操作方法：

作用	遇到错误抛异常	遇到错误返回特殊值
入队	public boolean add(E e)	public boolean offer(E e)
出队	public boolean remove(Object o)	public E poll()
获取优先级最高的元素	public E element()	public E peek()

PriorityQueue其他常用方法：

方法	类型	作用
public boolean contains(Object o)	普通方法	判断优先队列中是否包含对象o
public Object[] toArray()	普通方法	优先队列转数组
public int size()	普通方法	获取优先队列元素个数
public void clear()	普通方法	清空优先队列

2.3简单实现优先队列的基本操作

优先队列是基于堆实现的，本次使用大根堆来实现入队，出队，获取队头元素等基本操作。

入队：
步骤：

1. 将元素放入堆尾。
2. 对堆尾的结点进行向上方向调整，因为入队一个元素后，堆中只有一条到新插入结点路径上不是大根堆，所以仅需对该结点进行向上调整，所谓向上调整就是比较调整结点与父亲结点值的大小，以大根堆为例，如果该结点值比较大，则与父亲结点交换值，否则不需调整，该堆已经满足大根堆条件，因为交换后不知道上面的子树是否为大根堆，所以需要对交换路径上所有的结点进行相同的向上调整，直到调整完堆顶，过程中出现父亲结点比较大则结束调整，反之如果是小根堆，就把调整结点与父亲结点的比较方式改变一下即可。
3. 入队完成。

堆的结构：

public class Heap {
    private int[] elem;
    private int usedSize;
    public Heap() {
        this.elem = new int[10];
    }
        /**
     *
     * @param arr 目标交换数组对象
     * @param index1 下标1
     * @param index2 下标2
     */
    private void swap(int arr[], int index1, int index2) {
        int tmp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = tmp;
    }
    //基本操作方法
}

代码实现（基于大根堆）：

//判断队列是否满或空
    public boolean isFull() {
        return this.elem.length == this.usedSize;
    }
    public boolean idEmpty() {
        return this.usedSize == 0;
    }

//向上调整
    private void shiftUp(int child) {
        int parent = (child - 1) / 2;
        while (child > 0) {
            if (this.elem[parent] < this.elem[child]) {
                swap(this.elem, parent, child);
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

    /**
     * 基于大堆的优先队列进队
     */
    public void offer(int val) {
        if (isFull()) {
            this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);
        }
        //1.将元素插入堆尾
        this.elem[usedSize++] = val;
        //2.重新调整为大堆：向上调整
        shiftUp(usedSize - 1);
    }

出队：
步骤：

1. 将堆顶元素与堆尾元素交换，保存并删除堆尾元素。
2. 对堆顶元素向下调整，因为堆顶交换元素的路径可能会破坏大根堆（或小根堆）。
3. 返回之前保存的堆尾元素，即原优先队列队头元素。

实现代码（基于大根堆）：

    /**
     * 基于大堆的优先队列出队
     * @return 堆顶元素
     */
    public int poll() {
        if (idEmpty()) {
            throw new RuntimeException("优先队列为空!");
        }
        //1.将堆顶元素与堆尾元素交换
        swap(this.elem, 0, usedSize - 1);
        //2.保存原堆顶元素的值，并删除堆中原堆顶元素的值
        int ret = this.elem[--usedSize];
        //3.调整堆顶为根结点的树，使其调整为大堆
        shiftDown(0, usedSize);
        return ret;
    }

获取队头元素：
会出队，那获取队头元素就不在话下了。
实现代码：

    /**
     * 获取优先队列（基于大堆）队头元素
     * @return 堆顶元素
     */
    public int peek() {
        if (idEmpty()) {
            throw new RuntimeException("优先队列为空!");
        }
        return this.elem[0];
    }

2.4堆排序

如果是基于升序排序，则使用大堆，基于降序排序，则使用小堆。
升序排序步骤：

1. 将数组转换成大根堆，使用索引end标记最后一个元素。
2. 将堆顶元素与end处元素交换，end--。
3. 对堆顶结点进行向下调整，调整的结点下标不大于end。
4. 重复2,3步骤，直到end<=0。

简单说，因为大根堆堆顶存放最大元素，每次将最大元素与end出元素交换，再调整end-1部分的堆，这样就能依次把最大的元素放在后面，降序排列使用小根堆也是这个道理。
例如对下面这一个数组进行升序排序：

转成大堆：

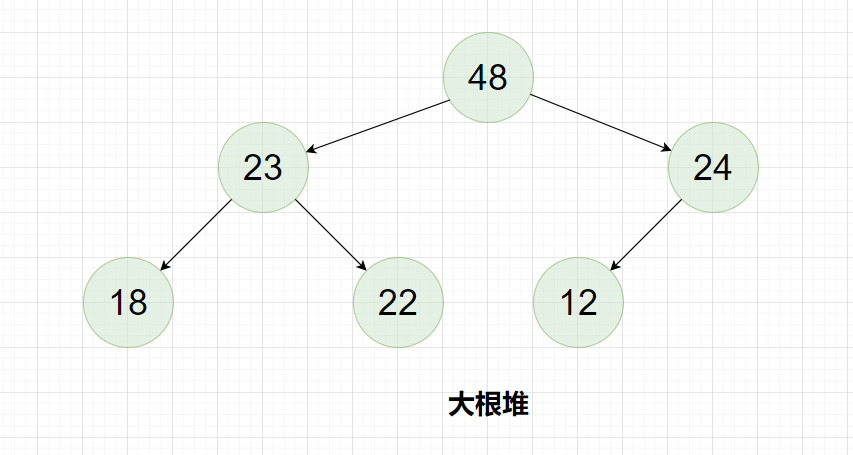
排序过程图解：
红色表示堆顶元素与end索引出元素交换。
蓝色表示已经排好序了。
黄色表示向下调整。


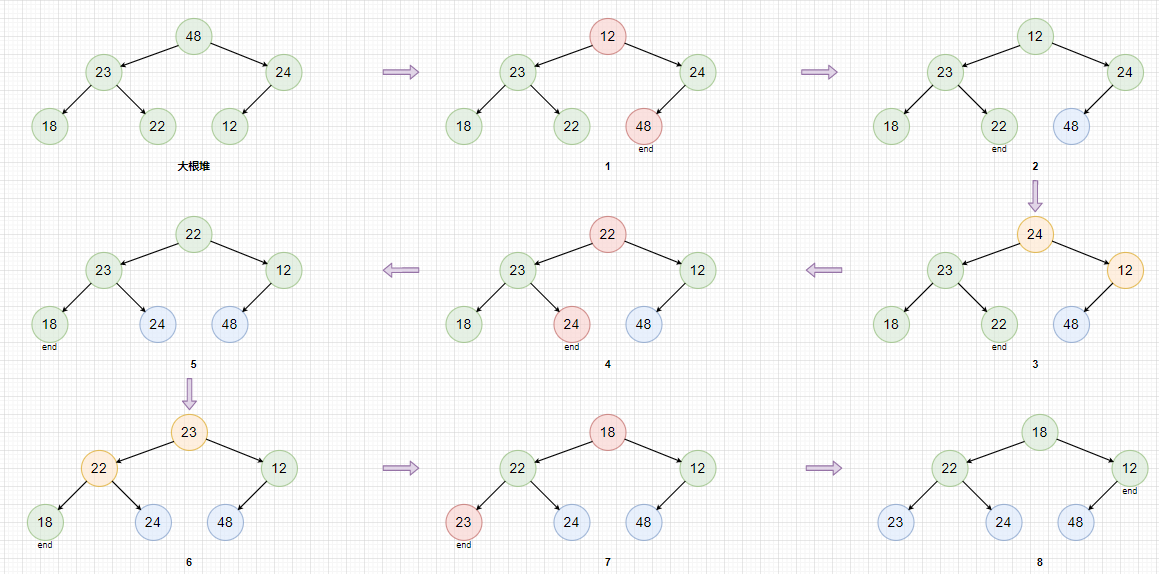
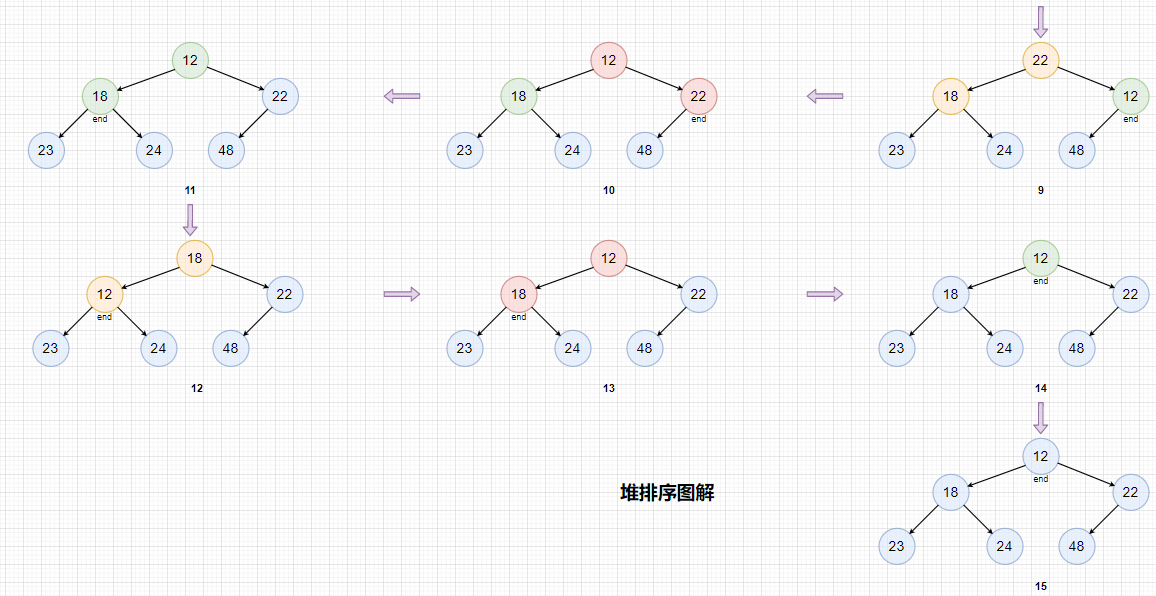
排序后数组为：

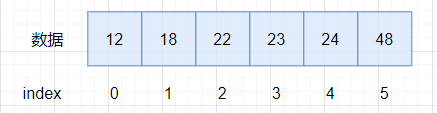
堆的结构：

public class Heap {
    private int[] elem;
    private int usedSize;
    public Heap() {
        this.elem = new int[10];
    }
        /**
     *
     * @param arr 目标交换数组对象
     * @param index1 下标1
     * @param index2 下标2
     */
    private void swap(int arr[], int index1, int index2) {
        int tmp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = tmp;
    }
    public void creatBigHeap(int[] data) {
        //拷贝数据
        this.elem = data;
        usedSize = data.length;
        //从最后一棵完全二叉树子树开始调整
        int child = this.usedSize - 1;
        int parent = (child - 1) / 2;

        while (parent >= 0) {
            shiftDown(parent, usedSize);
            parent--;
        }
    }
    /**
     * 向下调整
     * @param parent 父节点下标
     * @param len 堆大小
     */
    public void shiftDown(int parent, int len) {
        int child = 2 * parent + 1;
        while (child < len) {
            if (child + 1 < len && this.elem[child] < this.elem[child + 1]) {
                child++;
            }
            if (this.elem[child] > this.elem[parent]) {
                swap(this.elem, child, parent);
                parent = child;
                child = 2 * parent + 1;
            } else {
                break;
            }
        }
    }
}

升序堆排序：

    /**
     * 堆排序
     * @param arr 排序对象
     * @return 返回排序好的对象
     */
    public int[] heapSort(int[] arr) {
        creatBigHeap(arr);
        int end = usedSize - 1;
        for (int i = end; i > 0; i--) {
            swap(this.elem, 0, i);
            shiftDown(0,i);
        }
        return this.elem;
    }

3.TopK问题

topK问题指的是在一个很大数量级的数据中找出最大或者最小的前k个元素，比如在100万个数据中找到最大的10个数。

思路1： 先对数组排序再取前k个最值元素，不推荐，因为太慢了，只需要前k最值元素，没有必要对整个数组排序，况且数组元素个数是非常大的。

思路2： 使用堆，如求前k个最大的元素，可以创建一个基于大根堆的优先队列，将所有数据入队，再出队k个，这k个元素就是前k个最大的元素。

思路3： topK问题标准解决思路，topK问题的根本就是从一个大数量级的数组中找到最大或者最小的k个数，以求前k个最大元素为例，首先可以将数组前k个元素建成一个大小为k的小根堆，为什么是建造小根堆呢？因为堆顶元素是最小的，那么这个大小为k的小根堆堆顶元素top是这k个数字中最小的，然后遍历剩下的数组元素，如果比top大，就说明该元素可能是前k大的元素，此时的top一定不是前k个最大元素中的一员，使用该元素替换堆中的堆顶元素top，并重新调整为小根堆，遍历完数组后，这个大小为k的小根堆中的元素就是前k个最大的元素，简单说就是使用一个大小为k的堆来储存最大或最小的前k个元素。同理找前k个最小的元素需要使用大根堆，思路与求前k个最大元素是一样的。

我们来实现一下topK的代码，这里我们就不自己建堆了，我们使用java中的优先队列来实现，无参数构造的优先队列就是一个小根堆（默认）。

import java.util.Comparator;
import java.util.PriorityQueue;

public class TopK {
    /**
     * 求数组中最大k个元素
     * @param arr 数据
     * @param k 最大元素个数
     * @return 小根堆
     */
    public static PriorityQueue<Integer> topKMax(int[] arr, int k) {
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        if (k <= 0) return priorityQueue;
        for (int i = 0; i < arr.length; i++) {
            if (i < k) {
                priorityQueue.offer(arr[i]);
            } else {
                if (priorityQueue.isEmpty()) return priorityQueue;
                int top = priorityQueue.peek();
                if (arr[i] > top) {
                    //1.堆顶出队
                    priorityQueue.poll();
                    //2.入队并重新调整为小根堆
                    priorityQueue.offer(arr[i]);
                }
            }
        }
        return priorityQueue;
    }

    /**
     * 求前k个最小的元素
     * @param arr 数据
     * @param k 最小的元素个数
     * @return 大根堆
     */
    public static PriorityQueue<Integer> topKMin(int[] arr, int k) {
        //建大堆
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });
        if (k <= 0) return priorityQueue;
        for (int i = 0; i < arr.length; i++) {
            if (i < k) {
                priorityQueue.offer(arr[i]);
            } else {
                if (priorityQueue.isEmpty()) return priorityQueue;
                int top = priorityQueue.peek();
                if (arr[i] < top) {
                    //1.堆顶出队
                    priorityQueue.poll();
                    //2.入队并重新调整为大根堆
                    priorityQueue.offer(arr[i]);
                }
            }
        }
        return priorityQueue;
    }
    public static void main(String[] args) {
        int[] data = {3,2,4,5,6,1,7,9,8};
        PriorityQueue<Integer> ret = topKMax(data,3);//7,8,9
        System.out.print("前k个最大的元素：");
        System.out.println(ret);
        ret = topKMin(data, 3);
        System.out.print("前k个最小的元素：");
        System.out.println(ret);
    }
}

数组样例为int[] data = {3,2,4,5,6,1,7,9,8};k=3。

知道了topK问题解决问题，我们趁热打铁来看下面这一道题：
373. 查找和最小的 K 对数字
给定两个以 升序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。

示例 1:

输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数：
     [1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

示例 2:

输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释: 返回序列中的前 2 对数：
     [1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]

示例 3:

输入: nums1 = [1,2], nums2 = [3], k = 3 
输出: [1,3],[2,3]
解释: 也可能序列中所有的数对都被返回:[1,3],[2,3]

提示:

• 1 <= nums1.length, nums2.length <= 105
• -109 <= nums1[i], nums2[i] <= 109
• nums1 和 nums2 均为升序排列
• 1 <= k <= 1000

:bulb:解决思路：
其实这道题的思路与topK问题中求前k个最小元素的思路是一样的，只不过这里的元素是一个数对。
第一步，建造一个大根堆，大小为k，用来存放前k个和最小的数对。
第二步，注意到给定的两个目标数组都是升序排列的，如果k小于数组的长度，那么数对中的一个数一定在数组前k个元素中，遍历两数组min(k,len)的元素（其中len为数组长度），构造数对，将前k个数对放进大根堆，并调整。
第三步，遍历完按照第二步所构造的数对，如果数对和比堆顶数对和小，则替换堆顶的元素，最终大根堆中的数对就是最小的k组数字对。

public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        //构造大根堆
        PriorityQueue<List<Integer>> priorityQueue = new PriorityQueue(new Comparator<List<Integer>>() {
            @Override
            public int compare(List<Integer> o1, List<Integer> o2) {
                return o2.get(0) + o2.get(1) - o1.get(0) - o1.get(1);
            }
        });
        for (int i = 0; i < Math.min(k,nums1.length); i++) {
            for (int j = 0; j < Math.min(k, nums2.length); j++) {
                List<Integer> digits = new ArrayList<>();
                digits.add(nums1[i]);
                digits.add(nums2[j]);
                if (priorityQueue.size() < k) {
                    priorityQueue.offer(digits);
                } else {
                    int topAdd = priorityQueue.peek().get(0) + priorityQueue.peek().get(1);
                    if (digits.get(0) + digits.get(1) < topAdd) {
                        //1.出堆顶元素
                        priorityQueue.poll();
                        //2.入目标元素
                        priorityQueue.offer(digits);
                    } else {
                        //3.因为两个数组升序排列，此时如果比堆顶元素大，则后面的组合必然比堆顶元素大，此时应该直接结束循环
                        break;
                    }
                }
            }
        }
        //返回值是List所以先得将优先队列转换成List再返回
        List<List<Integer>> ret = new ArrayList(priorityQueue);
        return ret;
    }

其他练习题：
215. 数组中的第K个最大元素

堆与优先队列就介绍到这里了，下期再见！