数据结构与算法之二叉树遍历，深度与结点个数统计（实践上篇）

举报
未见花闻 发表于 2022/05/31 17:57:48 2022/05/31
【摘要】 本篇文章带大家认识数据结构——二叉树，树是一种非线性的数据结构，它是由有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

⭐️前面的话⭐️

本篇文章带大家认识数据结构——二叉树，树是一种非线性的数据结构，它是由有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创！
📆华为云首发时间：🌴2022年5月31日🌴
✉️坚持和努力一定能换来诗与远方！
💭参考书籍：📚《Java核心技术卷1》，📚《数据结构》，📚《Java编程思想》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

1.二叉树的基本操作

1.1回顾二叉树基本理论

一棵树上所有结点的度均不大于 2 2 ，则这棵树是一棵二叉树，空树是一棵特殊的二叉树。
一棵树是二叉树，其子树均为二叉树，二叉树的储存表示方法常用孩子表示法和孩子双亲表示法进行储存。

// 孩子表示法
class Node { 
	int val; // 数据域 
	Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树 
	Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树 
}
// 孩子双亲表示法
class Node { 
	int val; // 数据域 
	Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树 
	Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树 
	Node parent; // 当前节点的根节点 
}

二叉树都是由一下几种基本形态复合而成：

2-2

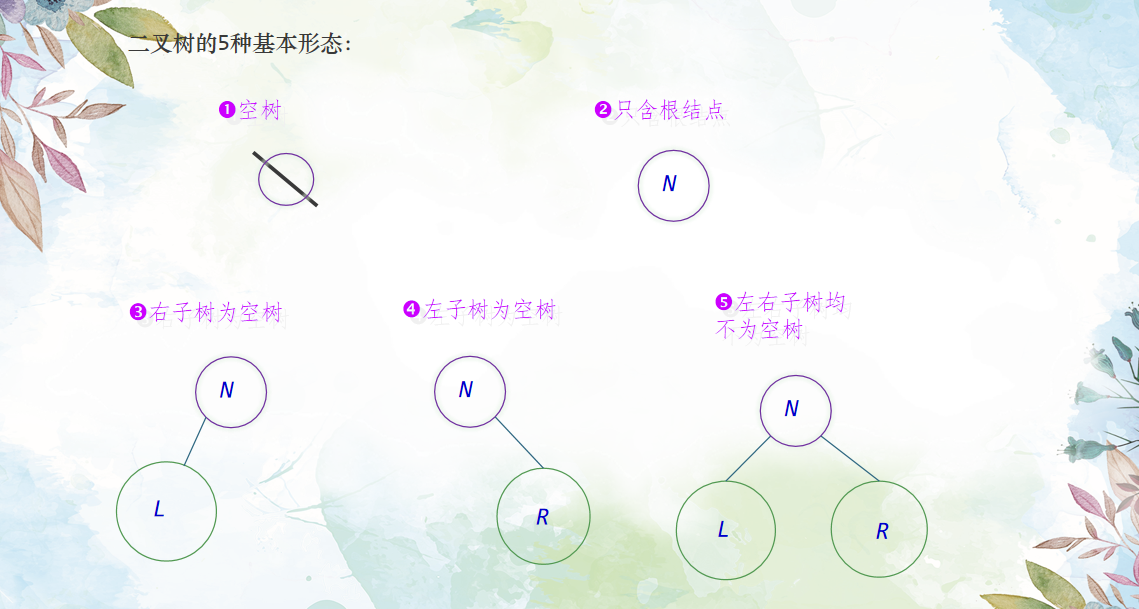
满二叉树与完全二叉树是二叉树的两种特殊情况。
满二叉树： 在一棵二叉树中，除叶子结点外，其他所有结点的度均为2，则该树为满二叉树。
2-3

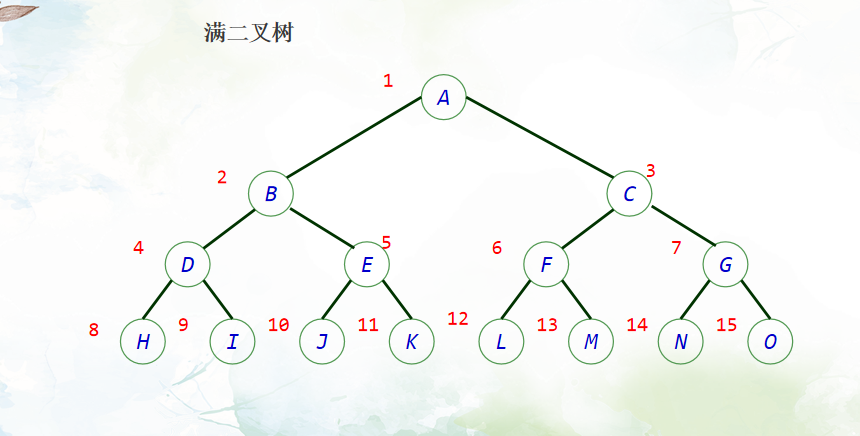
完全二叉树： 从根结点开始，每个非空结点按照层次依次递增，每层从左至右的顺序排列的二叉树，称为完全二叉树。换个说法，完全二叉树实际上是对应的满二叉树删除叶结点层最右边若干个结点得到的。

2-4
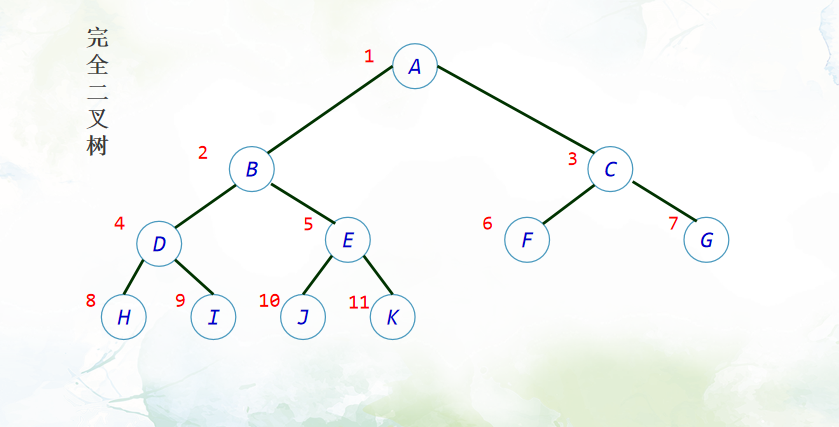
更多内容请参考：历史博文：树与二叉树（理论篇）

1.2二叉树的遍历

二叉树遍历是指按照一定次序访问树中所有结点，并且每个结点仅被访问一次的过程。
不论是前序遍历，中序遍历，还是后续遍历，二叉树的遍历所走的路径都是相同的，上述三者之间的区别只是获取根节点数据的时机不一样。
1-1
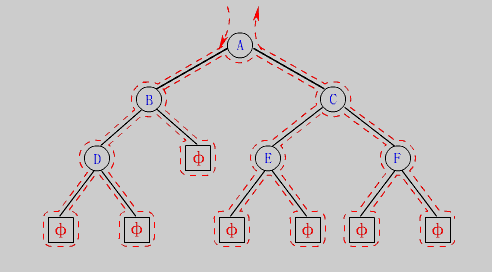
二叉树搜索路径：根->左子树->根->右子树，具体路径如上图。

二叉树结点结构：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

1.2.1前序遍历

所谓前序遍历，也叫做先序遍历，是按照二叉树搜索路径先获取根结点数据，再获取左子树数据，最后获取右子树数据。

前序遍历三部曲：

  1. 访问根结点；
  2. 前序遍历左子树；
  3. 前序遍历右子树。

如下图这样一棵二叉树：
1-2
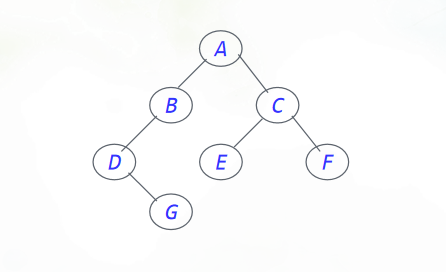
前序遍历的顺序是： A − > B − > D − > G − > C − > E − > F A->B->D->G->C->E->F

在线练习前序遍历：144. 二叉树的前序遍历

递归实现：
递归条件：如果结点root为空，则返回。
(1)获取并保存根结点数据。
(2)前序遍历左子树，并保存结果。
(3)前序遍历右子树，并保存结果。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if (root == null) return ret;//递归条件
        ret.add(root.val);//(1)
        ret.addAll(preorderTraversal(root.left));//(2)
        ret.addAll(preorderTraversal(root.right));//(3)
        return ret;
    }
}

非递归实现：
(1)使用一个栈储存前序遍历的结点。
(2)获取并保存非空结点数据，并将结点入栈。
(3)遍历的结点为空时，将结点刷新为栈顶元素的右结点，并出栈。
(4)重复上述步骤，直到栈和结点都为空。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();//(1)
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {    //(4)
            while (cur != null) {
                stack.push(cur);//(2)
                ret.add(cur.val);//(2)
                cur = cur.left;
            }
            TreeNode top = stack.pop();//(3)
            cur = top.right;//(3)
        }
        return ret;
    }
}

1.2.2中序遍历

所谓中序遍历，就是按照二叉树搜索路径先获取左子树数据，再获取根结点数据，最后获取右子树数据。

中序遍历三部曲：

  1. 中序遍历左子树；
  2. 访问根结点；
  3. 中序遍历右子树。

如下图这样一棵二叉树：
1-2
中序遍历的顺序是： D − > G − > B − > A − > E − > C − > F D->G->B->A->E->C->F

在线练习中序遍历：94. 二叉树的中序遍历

递归实现：
递归条件：如果结点root为空，则返回。
(1)中序遍历左子树，并保存结果。
(2)获取并保存根结点数据。
(3)中序遍历右子树，并保存结果。

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if (root == null) return ret;
        ret.addAll(inorderTraversal(root.left));//(1)
        ret.add(root.val);//(2)
        ret.addAll(inorderTraversal(root.right));//(3)
        return ret;
    }
}

非递归实现：
(1)使用一个栈储存中序遍历的结点。
(2)按照二叉树搜索顺序，将非空结点入栈。
(3)遍历的结点为空时，获取并保存结点的数据，并将结点刷新为栈顶元素的右结点，并出栈。
(4)重复上述步骤，直到栈和结点都为空。

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if (root == null) return ret;

        Stack<TreeNode> stack = new Stack<>();//(1)
        TreeNode cur = root;

        while (cur != null || !stack.isEmpty()) {       //(4)
            while (cur != null) {
                stack.push(cur);//(2)
                cur = cur.left;
            }
            TreeNode top = stack.pop();//(3)
            ret.add(top.val);//(3)
            cur = top.right;//(3)
        }
        return ret;
    }
}

1.2.3后序遍历

所谓后序遍历，就是按照二叉树搜索路径先获取右子树数据，再获取右子树数据，最后获取根结点数据。

后序遍历三部曲：

  1. 后序遍历左子树；
  2. 后序遍历右子树；
  3. 访问根结点。

如下图这样一棵二叉树：
1-2
后序遍历的顺序是： G − > D − > B − > E − > F − > C − > A G->D->B->E->F->C->A

在线练习后序遍历：145. 二叉树的后序遍历

递归实现：
递归条件：如果结点root为空，则返回。
(1)后序遍历左子树，并保存结果。
(2)后序遍历右子树，并保存结果。
(3)获取并保存根结点数据。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if (root == null) return ret;    //递归条件
        ret.addAll(postorderTraversal(root.left));//(1)
        ret.addAll(postorderTraversal(root.right));//(2)
        ret.add(root.val);//(3)
        return ret;
    }
}

非递归实现：
后序遍历的非递归实现需相比于前序遍历，中序遍历，要注意一个点，那就是要防止右子树多次遍历，如果不注意这一点那很有可能造成死循环。比如，就按照前序中序的思路，仅仅只改变数据获取的顺序，你会发现会出现一些问题，思路如下：
(1)使用一个栈储存前序遍历的结点。
(2)获取并保存非空结点数据，并将结点入栈。
(3)遍历的结点为空时，获取栈顶元素，判断栈顶的元素的右子树是否为空（相当于判断该树的右子树是否还需要遍历，如果右子树为空，那么表示该树左右子树都遍历完成，只需获取并保存根结点数据，否则需要遍历右子树）。
(4)如果不为空，更新当前结点为该结点的右结点，如果为空，将结点出栈，并保存当前结点数据。
(5)重复上述步骤，直到栈和结点都为空。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if (root == null) return ret;    

        Stack<TreeNode> stack = new Stack<>();//(1)
        TreeNode cur = root;
        
        while (cur != null || !stack.isEmpty()) {  //(5)
            while (cur != null) {
                stack.push(cur);                    //(2)
                cur = cur.left;
            }
            TreeNode top = stack.peek();
            if (top.right == null) {                //(3)
                ret.add(top.val);                   //(4)
                stack.pop();                        //(4)
            } else {                                //(3)
                cur = top.right;                    //(4)
            }
        }
        return ret;
    }
}

按照上述思路，得到上述代码，我们来运行看一看。
1-3
这就表示栈里面的元素太多了，使得超出了内存限制，大概率是死循环了。所以我们来分析分析思路的第(3)(4)点，先来看看这一段代码：

TreeNode top = stack.peek();
if (top.right == null) {                //(3)
	ret.add(top.val);                   //(4)
	stack.pop();                        //(4)
} else {                                //(3)
	cur = top.right;                    //(4)
}

我们试着模拟不难发现，当遍历完一个结点的右子树后，top又重新指向了该结点，然后又重复判断，得到的结果都是右子树不为空，最终一直对右子树重复遍历，为了解决这个问题，我们可以先标记遍历完后的右子树根结点，记为prev，当下一次top结点又回到这棵右子树的父结点，如果此时该结点的右子树为空或者prev与该结点右子树的根结点相同，就表示右子树已经遍历完成了，不需要再次遍历，将栈出栈，保存当前结点的数据，并将当前结点使用prev记录，以标识该结点已经遍历过。简单来说，还缺少了是否出栈的条件，这个条件一是该结点的右子树为空，二是该结点的右子树与上次标记的结点相同，只要满足上述两个条件之一，该结点的数据就可以获取，并标记已经完成遍历。

对上述思路进行优化得到：
(1)使用一个栈储存前序遍历的结点，定义二叉树结点prev，用来存放上一次遍历的右子树。
(2)获取并保存非空结点数据，并将结点入栈。
(3)遍历的结点为空时，获取栈顶元素，判断栈顶的元素的右子树是否为空和判断该元素的右子树是否与上一次遍历的右子树prev相等（相当于判断该树的右子树是否还需要遍历，如果右子树为空或者该结点的右子树与上一次遍历的结点相等，那么表示该树左右子树都遍历完成，只需获取并保存根结点数据和标识该结点已经被遍历，否则需要遍历右子树）。
(4)如果不为空或者prev与当前结点右子树不相同，更新当前结点为该结点的右结点，并使用prev记录该结点，如果为空或者prev与右子树根结点相同，将结点出栈，并保存当前结点数据和标记该结点已被遍历。
(5)重复上述步骤，直到栈和结点都为空。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if (root == null) return ret;    

        Stack<TreeNode> stack = new Stack<>();//(1)
        TreeNode cur = root;
        TreeNode prev = null;						//用来标记最近一次已经遍历的结点
        while (cur != null || !stack.isEmpty()) {  //(5)
            while (cur != null) {
                stack.push(cur);                    //(2)
                cur = cur.left;
            }
            TreeNode top = stack.peek();
            if (top.right == null || top.right == prev) {      //(3)
                ret.add(top.val);                   //(4)
                stack.pop();                        //(4)
                prev = top;                         //(4)
            } else {                                //(3)
                cur = top.right;                    //(4)
            }
        }
        return ret;
    }
}

其实上述前中后序遍历的递归就是深度优先搜索(DFS)。

1.3二叉树的结点个数

二叉树结点的泛型定义：

class TreeNode<E> {
    public E val;
    public TreeNode<E> left;
    public TreeNode<E> right;
    public TreeNode() {}
    public TreeNode(E val) {
        this.val = val;
    }
    public TreeNode(E val, TreeNode<E> left, TreeNode<E> right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

泛型二叉树前中后序遍历代码（思路与非泛型都一样）：

    // 前序遍历
    List<E> preOrder(TreeNode<E> root) {
        if (root == null) return new ArrayList<E>();
        List<E> ret = new ArrayList<>();
        ret.add(root.val);
        ret.addAll(preOrder(root.left));
        ret.addAll(preOrder(root.right));
        return ret;
    }
    // 中序遍历
    List<E> inOrder(TreeNode<E> root) {
        if (root == null) return new ArrayList<E>();
        List<E> ret = new ArrayList<>(inOrder(root.left));
        ret.add(root.val);
        ret.addAll(inOrder(root.right));
        return ret;
    }
    // 后序遍历
    List<E> postOrde(TreeNode<E> root) {
        if (root == null) return new ArrayList<E>();
        List<E> ret = new ArrayList<>(postOrde(root.left));
        ret.addAll(postOrde(root.right));
        ret.add(root.val);
        return ret;
    }

1.3.1统计整棵二叉树的结点个数

遍历一遍二叉树，对二叉树非空结点计数，前中后序遍历均可。

// 获取树中节点的个数
    int size(TreeNode<E> root) {
        if (root == null) return 0;
        return 1 + size(root.left) + size(root.right);
    }

1.3.2统计二叉树叶子结点个数

递归思路：

  1. 如果结点为空，表示该树没有结点返回0，
  2. 如果结点的左右子树都为空，表示该结点为叶子结点，返回1。
  3. 一棵二叉树的叶子结点数为左右子树叶子结点数之和。
// 获取叶子节点的个数
    int getLeafNodeCount(TreeNode<E> root) {
        if (root == null) return 0;
        if (root.left == null && root.right == null) return 1;
        return getLeafNodeCount(root.left) + getLeafNodeCount(root.left);
    }

1.3.3统计二叉树第k层次的结点个数

当k=1时，表示第一层次的结点个数，结点个数为1，每递进一层，k就会减1，那么一棵二叉树第k层结点数为左子树，右子树第k-1层次的结点数之和。
递归思路：

  1. 如果结点为空，返回0，k为1，返回1。
  2. 一棵二叉树第k层结点数为左子树，右子树第k-1层次的结点数之和。
// 获取第K层节点的个数
    int getKLevelNodeCount(TreeNode<E> root, int k) {
        if (root == null || k <= 0) return 0;
        if (k == 1) return 1;//第一层结点数为1，每递归一层·k--
        return getKLevelNodeCount(root.left, k-1) + getKLevelNodeCount(root.right, k-1);
    }

1.4获取二叉树的深度

1.4.1最深深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

示例：

给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7
返回它的最大深度 3 。

在线练习：
104. 二叉树的最大深度
剑指 Offer 55 - I. 二叉树的深度

🎉解题思路：

递归思路：

  1. 如果根结点为空，则这棵树的高度为0，返回0。
  2. 一棵二叉树的最深深度即为左右子树深度的最大值加上1。
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
}

1.4.2最浅深度

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [ 0 , 1 0 5 ] [0, 10^5] 内
− 1000 < = N o d e . v a l < = 1000 -1000 <= Node.val <= 1000

在线练习：
111. 二叉树的最小深度

🎉解题思路：
对于最小深度首先要注意一点，当一个结点的左子树或者右子树为空时，最小深度并不是0，而是不为空的那颗子树的最小深度加上1。
比如，如图所示这样一棵树，它的最小深度是4，而不是1。
1-4
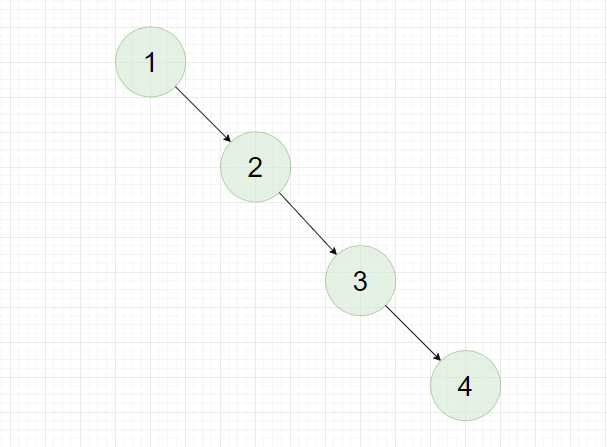
这道题可以使用递归，递归思路：

  1. 根结点为空，该树最小高度为0，返回0。
  2. 根结点的左右子树至少有一个是空，则该树的最小高度为另一棵子树的最小高度加1。
  3. 该根结点左右子树都不为空，则该树最小高度为左右子树最小高度的最小值加1。
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) return 0;//1
        if (root.left == null) return minDepth(root.right) + 1;//2
        if (root.right == null) return minDepth(root.left) + 1;//2
        return Math.min(minDepth(root.left), minDepth(root.right)) + 1;//3
    }
}

1.5在二叉树中寻找目标值

使用二叉树前序遍历搜索即可，中序后序都可。

// 检测值为value的元素是否存在
    TreeNode<E> find(TreeNode<E> root, E val) {
        if (root == null) return null;
        if (root.val.equals(val)) return root;
        TreeNode<E> leftRet = find(root.left, val);
        TreeNode<E> rightRet = find(root.right, val);
        return leftRet != null ?  leftRet : rightRet;
    }

1.6层序遍历

1.6.1判断二叉树是否为完全二叉树

完全二叉树： 从根结点开始，每个非空结点按照层次依次递增，每层从左至右的顺序排列的二叉树，称为完全二叉树。换个说法，完全二叉树实际上是对应的满二叉树删除叶结点层最右边若干个结点得到的。

2-4

判断一棵树是否是完全二叉树，我们可以设计一个队列，从根节点开始，每次将根节点的左右孩子结点（包括空结点）依次入队，然后获得队列对头元素并出队，将出队这个结点的左右孩子结点（包括空结点）依次入队，以此类推，直到获取的结点为空，获取的结点为空后，结束上述操作，判断队列中的所有元素是否为空，如果为空，就表示这棵二叉树为完全二叉树。

// 判断一棵树是不是完全二叉树
    boolean isCompleteTree(TreeNode<E> root) {
        if (root == null) return true;
        Queue<TreeNode<E>> queue = new LinkedList<>();
        TreeNode<E> cur = root;
        while (cur != null) {
            queue.offer(cur.left);
            queue.offer(cur.right);
            cur = queue.poll();
        }
        while (!queue.isEmpty()) {
            if (queue.poll() != null) return false;
        }
        return true;
    }

1.6.2层序遍历

对于二叉树的层序遍历，它的实现思路与判断一棵二叉树是否是完全二叉树思路十分相似，都是使用队列来进行实现，但是入队时有一点不同，那就是如果结点为空，则不需要入队，直到最终队列和当前结点均为空时，表示遍历结束。

在线练习：102. 二叉树的层序遍历
对于上面这道题，层序遍历还需要将每层的元素分开，单独存入List中，为了解决这个问题，可以在每次获取出队元素前，先获取队列中元素个数，这个元素个数就是当前层次的元素个数，这样就能把每层的元素都分开了。
（1）记录当前队列元素个数，即二叉树每层的元素个数。
（2）将此层二叉树的结点的左右非空孩子结点存于队列中，并将该层二叉树结点的值存于顺序表中。
（3）将非空的子结点存入队列中。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<>();
        if (root == null) {
            return ret;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();//（1）
            List<Integer> list = new ArrayList<>();//用与存放该层二叉树结点的值
            while (size > 0) {
                TreeNode cur = queue.poll();//（2）
                list.add(cur.val);
                //（3）
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
                size--;
            }
            ret.add(list);
        }
        return ret;
    }
}

像这种层序遍历的思路就是 广度优先搜索(BFS) 的思路。

【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
Java 二叉树 数据结构
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入