⭐️前面的话⭐️

本篇文章带大家认识Java集合——Queue,LinkedList，Queue就是队列的意思，是一种数据结构，又叫先进先出表，本文首先会介绍数据结构《队列》，了解清楚队列的特点与性质，双端队列，循环队列，然后会根据队列的性质简单来模拟队列最后介绍集合框架Queue,Deque接口,LinkedList类常见方法的使用。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创！
📆华为云首发时间：🌴2022年5月31日🌴
✉️坚持和努力一定能换来诗与远方！
💭参考书籍：📚《Java核心技术卷1》，📚《数据结构》，📚《Java编程思想》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

---

题外话：在正式开始之前，我们先来看一看集合框架，画上√的表示博主已经介绍完毕了，可以翻看JavaSE系列专栏进行寻找，画上⭐️表示本文所介绍的内容。

---

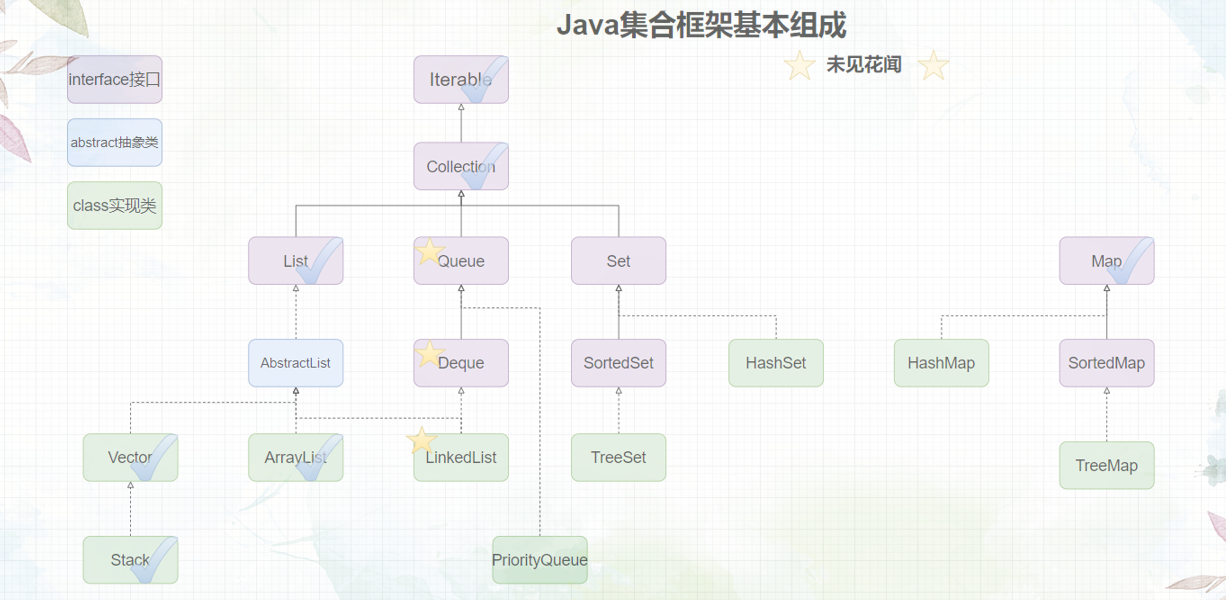
1.队列

1.1队列的概念与特点

队列又称队，是一种线性表， 队列只能选取一个端点进行插入操作，另一个端点进行删除操作，所以先进去的元素先出来，所以队列也称为先进先出表。

队列的几个术语：

• [x] 进行插入的一端称做队尾（rear）。
• [x] 进行删除的一端称做队首或队头（front）。
• [x] 向队列中插入新元素称为进队或入队，新元素进队后就成为新的队尾元素。
• [x] 从队列中删除元素称为出队或离队，元素出队后，其后继元素就成为队首元素。

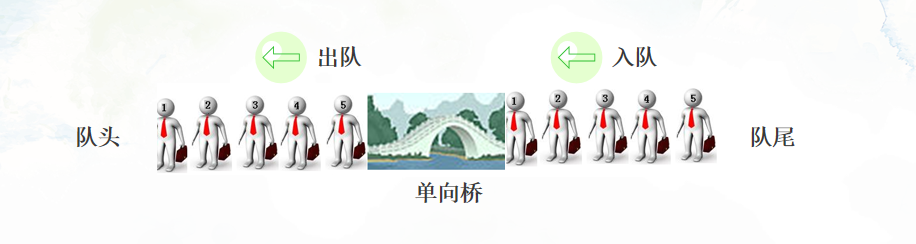
形象来说，队列就是一个单向桥，进桥叫做入队，出桥叫做出队。

1.2双端队列与循环队列

1.2.1双端队列

双端队列是指两端都可以进行进队和出队操作的队列，将队列的两端分别称为前端和后端，两端都可以入队和出队。

所以双端队列既能够当队列使用，也能当栈使用，Java底层是使用双链表(LinkedList)来实现双端队列(Deque)和队列(Queue)的。

限制一端进行出队或入队的双端队列称为受限的双端队列。

1.2.2循环队列

队列可以使用链表实现，那可不可以使用顺序表实现呢？当然可以，如果使用顺序表实现，有一个问题，那就是顺序表空间利用不充分，因为每次出队都会浪费一个空间，为了解决这个问题，可以采用循环队列，这样入队时能够重新从顺序表的尾部跳到顺序表头部对已经出队的空间重新利用，这样就能够保证顺序表的每一个空间都能有机会被利用。

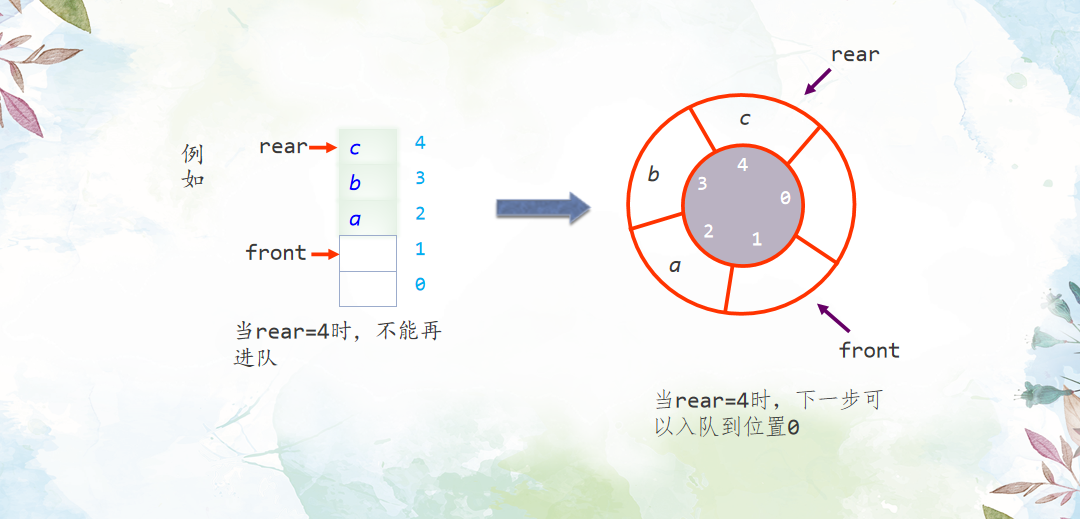
但是有一个问题，如何确定队列是空还是满？
不妨设对头索引为front，队尾索引为rear，顺序表长度为len。

方式1：记录队列元素个数size，当size的值与顺序表的大小相等时，代表队列已满。size值为0表示队列为空。
方式2：使用一个boolean类型的成员变量flag标记，初始为false，当每次入队时将flag设置为true，出队将flag设置为false，当rear == front && flag == true表示队列已满，当rear == front && flag == false表示队列为空。
方式3：牺牲一个单位的空间，在每次入队前判断（rear+1）% len是否与front相等，如果相等表示队列已满，如果rear == front则表示队列为空。

比如我按照方式1创建循环队列，大小为8，如图，size=0为空队列，size=8为满队列。

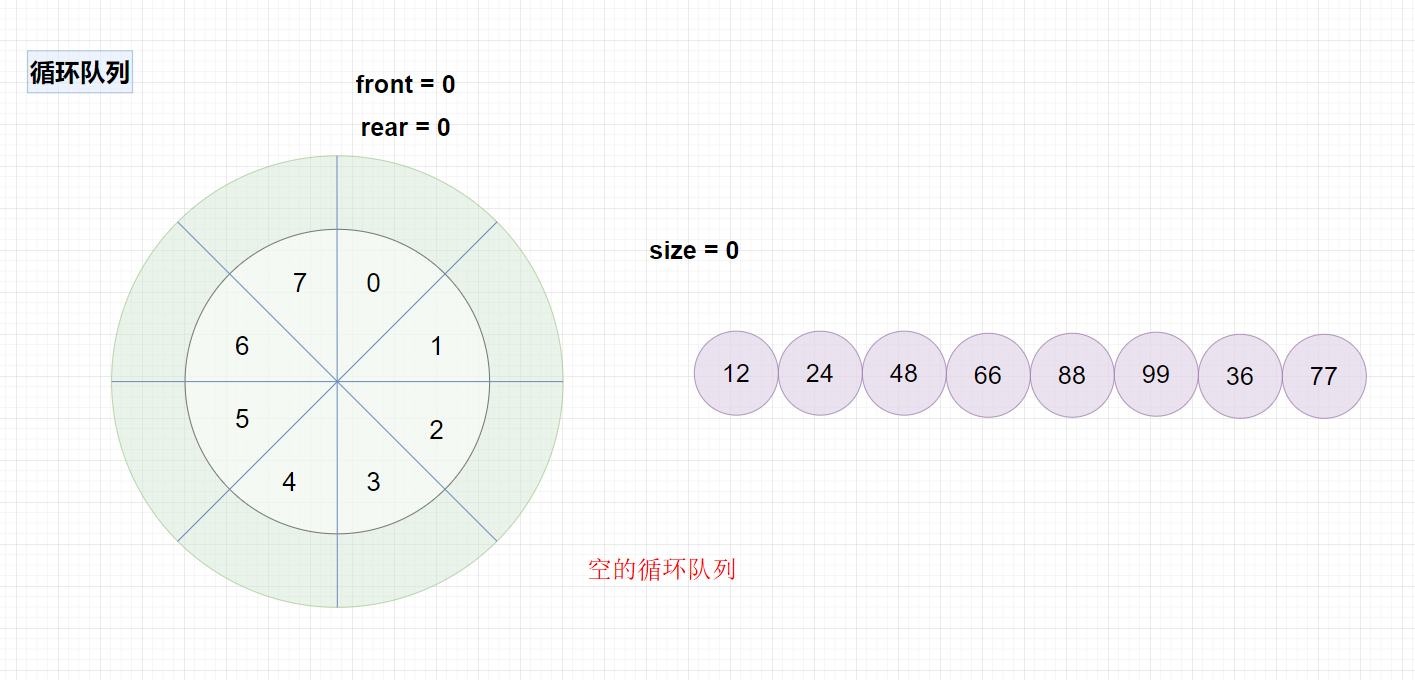
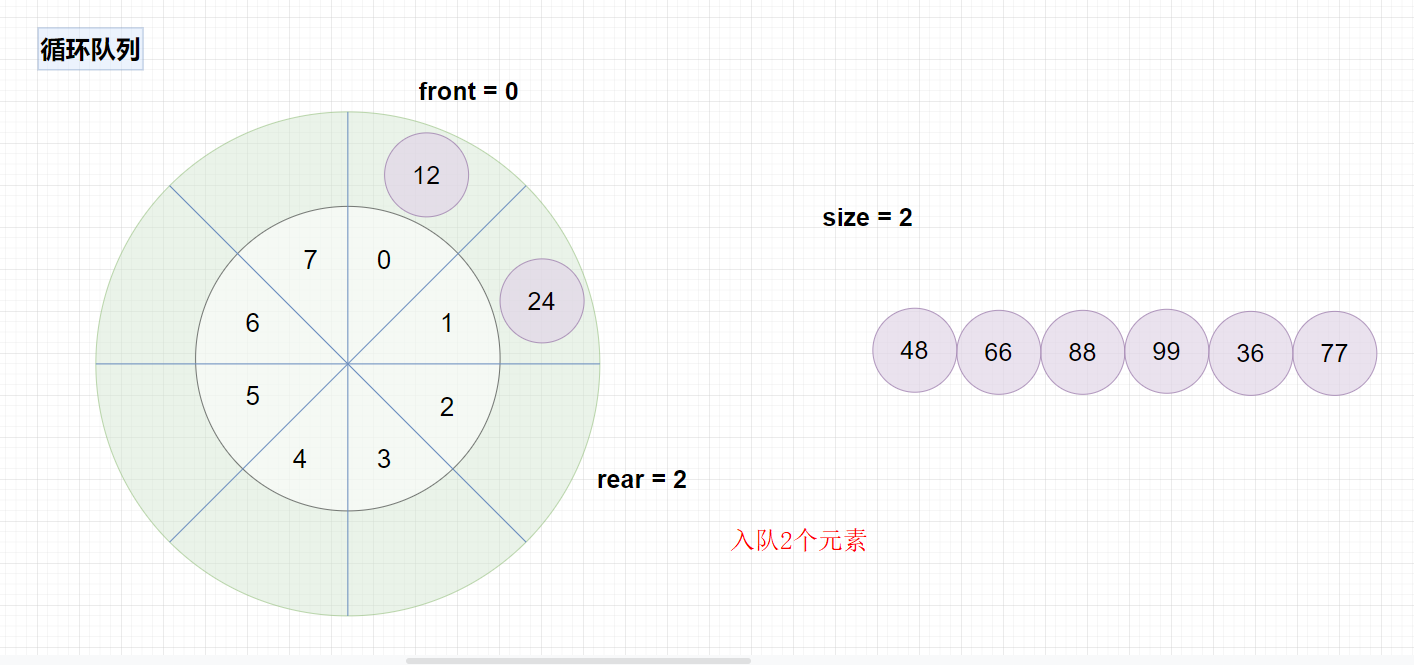
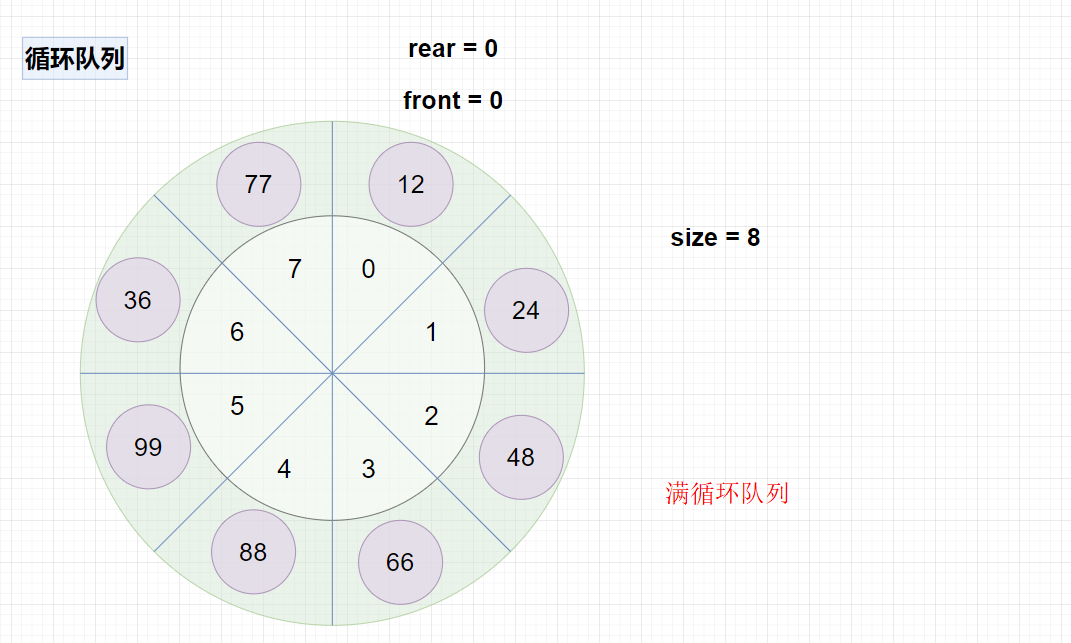
2.集合框架之Queue,Deque,LinkedList

2.1Queue,Deque接口与LinkedList类

我们先来看这三者之间的关系：

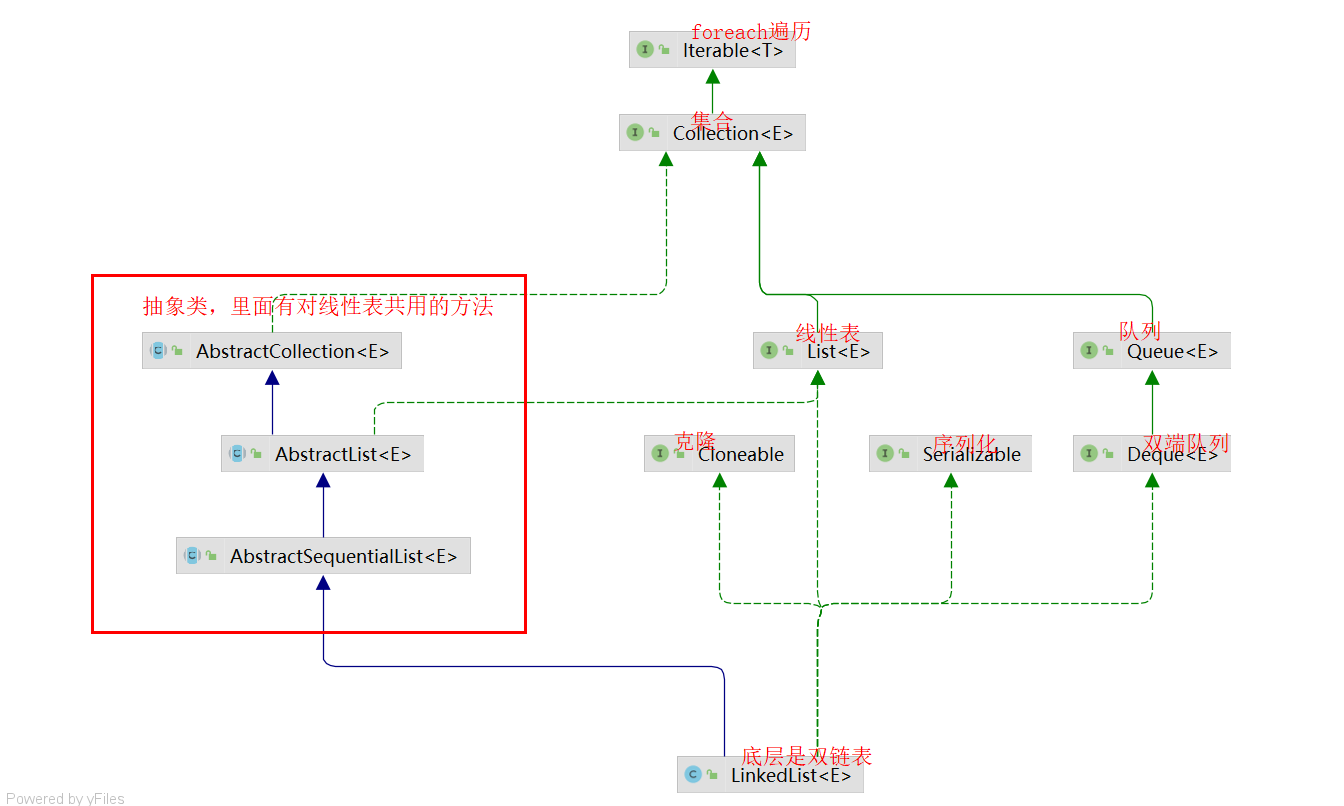
LinkedList类实现了Queue,Deque接口，Deque接口扩展了Queue接口，三者都扩展或继承了Collection和Iterable接口。

2.1.1LinkedList类

LinkedList类底层是由双链表实现的，所以从本质上来说LinkedList类就是双链表，双链表可以实现栈，队列，双端队列，树，二叉树等数据结构，由此LinkedList类可以当做链表，可以当做栈，可以当做队列等等，用途广泛，我们来看看该类下面常用的方法吧（实现Queue,Deque接口的方法不列举了）：

方法	类型	作用
public LinkedList()	构造方法	新建一个LinkedList对象
public LinkedList(Collection<? extends E> c)	构造方法	根据集合对象创建LinkedList对象
public boolean contains(Object o)	普通方法	判断LinkedList对象中是否包含o元素
public int size()	普通方法	获取LinkedList对象中元素的数目
public boolean add(E e)	普通方法	尾插一个元素e
public void add(int index, E element)	普通方法	在索引为 index处插入元素element
public boolean remove(Object o)	普通方法	删除LinkedList对象中第一个元素
public E remove(int index)	普通方法	删除索引为index处的元素
public boolean addAll(Collection<? extends E> c)	普通方法	根据所给的集合对象尾插集合对象中所有的元素
public boolean addAll(int index, Collection<? extends E> c)	普通方法	根据所给的集合对象在索引为index位置插入集合对象中所有的元素
public void clear()	普通方法	清空LinkedList对象中所有的元素
public E get(int index)	普通方法	获取索引为index处的元素
public E set(int index, E element)	普通方法	将索引index处的元素修改为element
public int indexOf(Object o)	普通方法	返回此列表中指定元素o的第一次出现的索引，如果此列表不包含元素，则返回-1。
public int lastIndexOf(Object o)	普通方法	返回此列表中指定元素的最后一次出现的索引，如果此列表不包含元素，则返回-1。
public ListIterator<E> listIterator(int index)	普通方法	从列表中的指定位置index开始，返回此列表中元素的列表迭代器（按适当的顺序）。
public Object clone()	普通方法	克隆一个LinkedList对象
public Object[] toArray()	普通方法	以正确的顺序（从第一个到最后一个元素）返回一个包含此列表中所有元素的数组
public <T> T[] toArray(T[] a)	普通方法	以正确的顺序返回一个包含此列表中所有元素的数组（从第一个到最后一个元素）; 返回的数组的运行时类型是指定数组的运行时类型
public Spliterator<E> spliterator()	普通方法	在此列表中的元素上创建late-binding和故障快速 Spliterator

对象创建：

LinkedList<元素对象类型> 变量名 = new LinkedList<>();

具体得方法就不演示怎么使用了，小伙伴们根据需要选择正确的方法使用即可。

2.1.2Queue,Deque接口

Queue接口提供了队列增删查改等基本操作的方法，Deque接口提供了双端队列操作的一系列方法，LinkedList类实现了Queue,Deque接口，因此可以使用Queue引用LinkedList对象当队列使用，Deque引用LinkedList对象当双端队列使用，当然也可以直接使用LinkedList引用LinkedList对象当队列，双端队列，双链表等数据结构使用。

Queue接口中常用的方法：

方法	作用
boolean add(E e)	队尾入队，入队失败引发异常
boolean offer(E e)	队尾入队，入队失败不引发异常（推荐）
E remove()	对头出队，并返回队头元素，出队失败引发异常
E poll()	对头出队，并返回队头元素，出队失败不引发异常（推荐）
E element()	获取队头元素，获取失败引发异常
E peek()	获取队头元素，获取失败不引发异常（推荐）

Deque接口中常用的方法：

方法	作用
void addFirst(E e)	在双端队列队头插入元素e，失败引发异常
void addLast(E e)	在双端队列队尾插入元素e，失败引发异常
boolean add(E e)	在双端队列队尾插入元素e，失败引发异常
boolean offerFirst(E e)	在双端队列队头插入元素e，失败不引发异常
boolean offerLast(E e)	在双端队列队尾插入元素e，失败不引发异常
boolean offer(E e)	在双端队列队尾插入元素e，失败不引发异常
E removeFirst()	在双端队列队头删除元素e，并返回，失败引发异常
E removeLast()	在双端队列队尾删除元素e，并返回，失败引发异常
E remove()	在双端队列队头删除元素e，并返回，失败引发异常
E pollFirst()	在双端队列队头删除元素e，并返回，失败返回null
E pollLast()	在双端队列队尾删除元素e，并返回，失败返回null
E poll()	在双端队列队头删除元素e，并返回，失败返回null
E getFirst()	获取队头元素，deque为空，会抛出异常
E getLast()	获取队尾元素，deque为空，会抛出异常
E element()	获取队头元素，deque为空，会抛出异常
E peekFirst()	获取队头元素，deque为空，返回null
E peekLast()	获取队尾元素，deque为空，返回null
E peek()	获取队头元素，deque为空，返回null
boolean removeFirstOccurrence(Object o)	从队头到队尾，寻找并删除第一次出现的元素o，如果deque包含o元素返回true，没找到返回false，失败引发异常
boolean removeLastOccurrence(Object o)	从队头到队尾，寻找并删除最后一次出现的元素o，如果deque包含o元素返回true，没找到返回false，失败引发异常
boolean remove(Object o)	从队头到队尾，寻找并删除第一次出现的元素o，如果deque包含o元素返回true，没找到返回false，失败引发异常
void push(E e)	在deque对象队头插入元素e，失败引发异常
E pop()	在deque对象队头删除并返回元素e，失败引发异常
boolean contains(Object o)	判断双端队列中是否包含元素o，包含返回true，不包含返回false
int size()	获取双端队列元素个数
Iterator<E> iterator()	以正确的顺序返回此deque中的元素的迭代器。 元素将按照从头（头）到最后（尾）的顺序返回。
Iterator<E> descendingIterator()	以相反的顺序返回此deque中的元素的迭代器。 元素将从最后（尾）到第一（头）的顺序返回。

add系列方法与offer系列方法的区别：
两者都是在队列队头或队尾插入元素，前者（add）插入元素失败会引发异常，后者（offer）插入元素失败不会引发异常，只会以返回false的形式表示插入元素失败，如果是有容量限制的队列，使用offer系列方法更加合适。

remove系列方法与poll系列方法的区别：
两者都是在队列队头或队尾删除并返回元素，前者（remove）删除元素失败会引发异常，后者（poll）删除元素失败不会引发异常，只会以返回null的形式表示删除元素失败，如果是有容量限制的队列，使用poll系列方法更加合适。

get系列方法与peek系列方法的区别：
两者都是在队列队头或队尾获取并返回元素，前者（get）获取元素失败会引发异常，后者（peek）获取元素失败不会引发异常，只会以返回null的形式表示获取元素失败，如果是有容量限制的队列，使用peek系列方法更加合适。

2.2队列的简单模拟

知道了队列的特点，我们就能来尝试自己实现一个队列，队列的实现方式有很多，java集合框架中，队列是利用双链表实现的，使用顺序表也可以实现，前面已经说过需要采用循环的方式来实现，单链表其实也可以实现队列，不过有个细节需要处理。

:key: 细节：采用单链表的头做队头还是单链表的尾做队头？
如果采用单链表的尾做队头，那么单链表的头就是队尾，因为队列是从队尾进，队头出，所以出队可以使用尾删，需要遍历到队尾，时间复杂度为O（N），入队采用头插法入队时间复杂度为O（1），就算再加上指向单链表尾部的尾指针，也不能够实现时间复杂度为O（1）的尾删，因为删除单链表结点，需要知道被删除结点的前一个结点。
如果采用单链表的头做队头，那么单链表的尾为队尾，因为队列是从队尾进，队头出，所以出队可以使用头删法，时间复杂度为O（1），入队需要遍历到队尾采用尾插法，时间复杂度为O（N），但是加上一个指向单链表尾结点的指针就能实现入队的时间复杂度为O（1）。
综上所述，将单链表的头做队尾，单链表的尾做队头是实现队列最佳方案。

如果使用双链表，上面这个细节就不需要考虑了，所以使用双链表实现队列比单链表更加简单，所以博主来尝试使用单链表实现队列，毕竟难一点的都会了，那么简单的那肯定就不成问题了。

单链表结点：

class ListNode<E> {
    public E val;
    public ListNode<E> next;
    public ListNode(E val) {
        this.val = val;
    }
}

实现队列：队尾入队offer，队头出队poll，获取队头元素peek，toString方法

public class MyQueue<E> {
    public ListNode<E> head;//指向单链表的头
    public ListNode<E> last;//指向单链表的尾

    public boolean offer(E e) {
        //队尾(单链表的尾)入队,尾插
        ListNode<E> node = new ListNode<>(e);
        if (isEmpty()) {
            this.head = node;
            this.last = node;
            return true;
        }
        this.last.next = node;
        this.last = node;
        return true;
    }
    public E poll() {
        //队头出队(单链表的头),头删
        if (isEmpty()) {
            return null;
        }
        ListNode<E> cur = this.head;
        this.head = cur.next;
        return cur.val;
    }
    public E peek() {
        //获取队头（单链表的头）的元素
        if (isEmpty()) {
            return null;
        }
        return this.head.val;
    }
    public boolean isEmpty() {
        return this.head == null;
    }

    @Override
    public String toString() {
        ListNode<E> cur = this.head;
        if (cur == null) {
            return "[]";
        }
        StringBuilder stringBuilder = new StringBuilder("[");
        while (cur.next != null) {
            stringBuilder.append(cur.val);
            stringBuilder.append(",");
            cur = cur.next;
        }
        stringBuilder.append(cur.val);
        stringBuilder.append("]");
        return stringBuilder.toString();
    }
}

测试代码：

public class Test {
    public static void main(String[] args) {
        MyQueue<Integer> myQueue = new MyQueue<>();
        myQueue.offer(24);
        myQueue.offer(48);
        myQueue.offer(86);
        myQueue.offer(98);
        myQueue.offer(100);
        System.out.println("入队offer[24,48,86,98,100]: "+ myQueue);
        System.out.println("出队poll:" + myQueue.poll());
        System.out.println("出队poll:" + myQueue.poll());
        System.out.println("出队poll:" + myQueue.poll());
        System.out.println("获取队头元素peek:" + myQueue.peek());
        System.out.println("队列中的元素:" + myQueue);
    }
}

运行结果：正常

2.3使用队列解决问题

2.3.1使用栈实现队列

题目：使用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：
实现 MyQueue 类：
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

提示：

$1 <= x <= 9$
最多调用 $100$次 $push、pop、peek 和 empty$
假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）
💡解题思路：
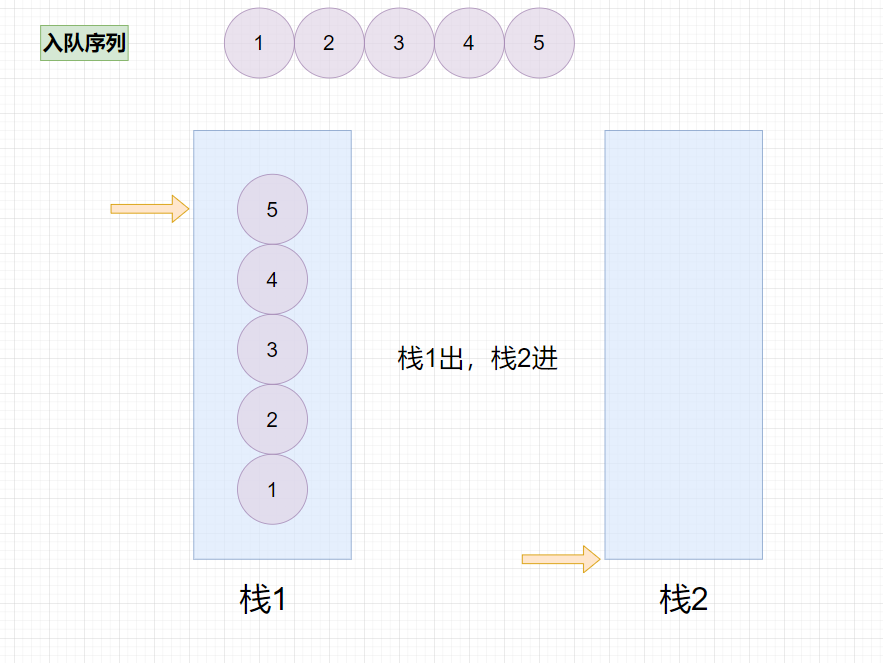
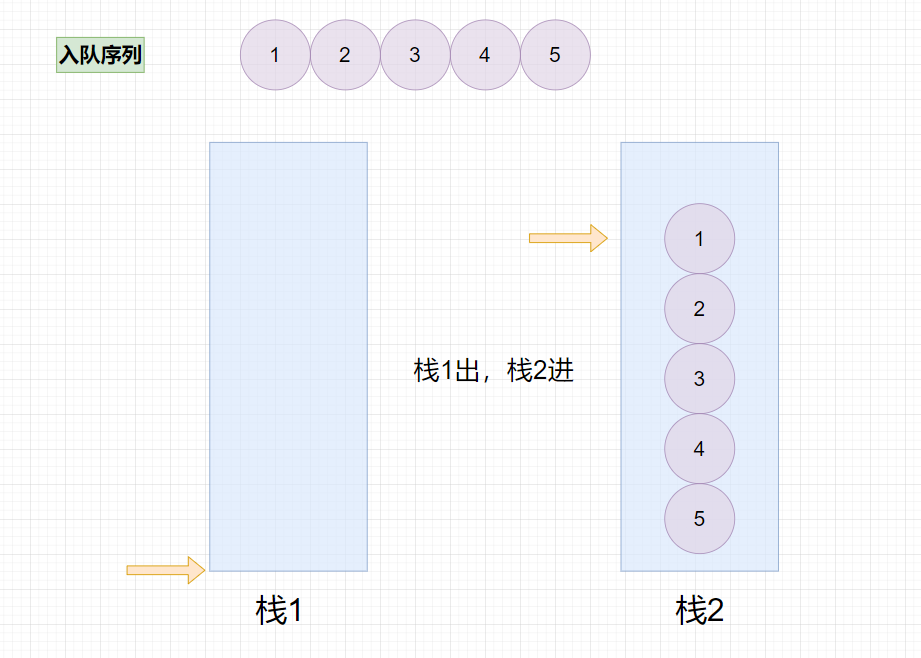
这道题要我我们使用栈来实现队列，栈是先进后出表，队列是先进先出表，显然只使用一个栈肯定是不能够解决问题的，因为栈中的所有元素进行两次出栈，最终出栈序列会与进栈序列相同，所以我们可以考虑两个栈来实现队列，分别称这两个栈为栈1，栈2。
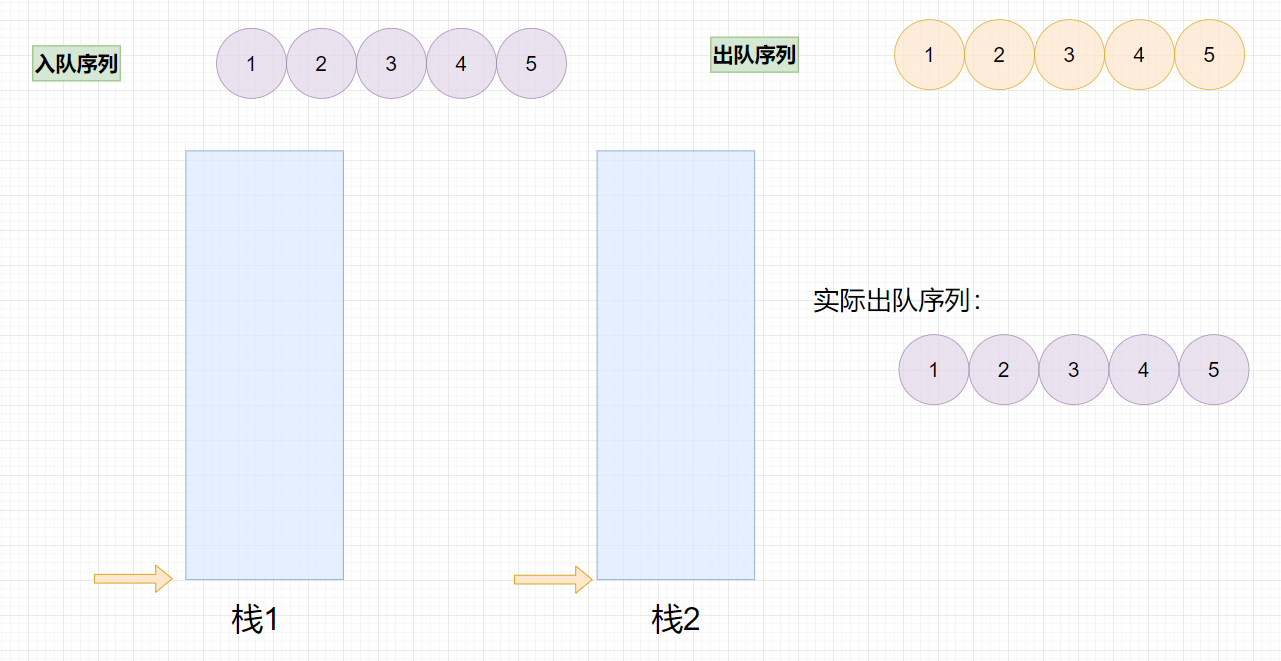
栈1用来入队，就是说入队的所有元素都往栈1里面放，出队在栈2执行，如果栈2是空的，则将栈1里面所有的元素出栈，放入栈2，这样从栈1入，栈2出的元素满足了先进先出的原则，队列也完成了实现。
当两个栈均为空时，表示队列为空。

🔑源代码：

class MyQueue {
    private Stack<Integer> stack1;
    private Stack<Integer> stack2;
    public MyQueue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }
    
    public void push(int x) {
        stack1.push(x);
    }
    
    public int pop() {
        if (empty()) return -1;
        if (stack2.isEmpty()) {
            int size = stack1.size();
            for (int i = 0; i < size; i++) {
                int val = stack1.pop();
                stack2.push(val);
            }
        }
        if (!stack2.isEmpty()) {
            return stack2.pop();
        }
        return -1;
    }
    
    public int peek() {
        if (empty()) return -1;
        if (stack2.isEmpty()) {
            int size = stack1.size();
            for (int i = 0; i < size; i++) {
                int val = stack1.pop();
                stack2.push(val);
            }
        } 
        if (!stack2.isEmpty()) {
            return stack2.peek();
        }
        return -1;
    }
    
    public boolean empty() {
        return stack1.isEmpty() && stack2.isEmpty();
    }
}

在线练习链接：
1.面试题 03.04. 化栈为队
2.剑指 Offer 09. 用两个栈实现队列
3.232. 用栈实现队列

2.3.2使用队列实现栈

题目：使用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。
实现 MyStack 类：
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

提示：

$1 <= x <= 9$
最多调用 $100$ 次 $push、pop、top 和 empty$
每次调用 pop 和 top 都保证栈不为空

进阶：你能否仅用一个队列来实现栈。

💡解题思路：

思路一：
使用两个队列，不妨记为队1，队2，进队和出队永远往非空队列操作，如果进队时两个队列均为空，则任选一个队列入队。
入栈时，哪一个队列不为空，就在哪一个队列入队。
出栈时，先找到不为空的队列，然后获取该队列的大小size，将前size-1个元素转移到另一个队列，剩下最后一个元素出队返回，这样保证了一个队列为空，另一个队列不为空。
获取栈顶元素，与出栈思路一样，不过需要将全部size元素转移。

思路二：
使用一个队列，队列是先进先出，栈是先进后出，在入栈前，我们先保存入队前的元素个数psize，然后进行新元素入队，最后将所有的旧元素重新入队（就是对所有的旧元素先出队再入队），这样做可以将旧元素（先进队列的元素）全部排在新元素（后进队的元素），这样在这个队列中，新元素总是能够排在队头，实现了栈的后进先出的特点。

🔑源代码：
思路一：两个栈

class MyStack {
    Queue<Integer> queue1;
    Queue<Integer> queue2;

    public MyStack() {
        this.queue1 = new LinkedList<>();
        this.queue2 = new LinkedList<>();
    }
    
    public void push(int x) {
        if (empty()|| !this.queue1.isEmpty()) {
            this.queue1.offer(x);
            return;
        }
        this.queue2.offer(x);
    }
    
    public int pop() {
        if (empty()) return -1;
        int size1 = this.queue1.size();//注意！不能在循环中获取队列大小，因为随着队列的改变，队列大小也会随着改变
        int size2 = this.queue2.size();
        if(!this.queue1.isEmpty()) {
            for (int i = 0; i < size1 - 1; i++) {
                int val = this.queue1.poll();
                this.queue2.offer(val);
            }
            return this.queue1.poll();
        } else {
            for (int i = 0; i < size2 - 1; i++) {
                int val = this.queue2.poll();
                this.queue1.offer(val);
            }
            return this.queue2.poll();
        }
    }
    
    public int top() {
        if (empty()) return -1;
        int val = -1;
        int size1 = this.queue1.size();//注意！不能在循环中获取队列大小，因为随着队列的改变，队列大小也会随着改变
        int size2 = this.queue2.size();
        if(!this.queue1.isEmpty()) {
            for (int i = 0; i < size1; i++) {
                val = this.queue1.poll();
                this.queue2.offer(val);
                System.out.println(val);
            }
            return val;
        } else {
            for (int i = 0; i < size2; i++) {
                val = this.queue2.poll();
                this.queue1.offer(val);
                System.out.println(val);
            }
            
            return val;
        }
    }
    
    public boolean empty() {
        return this.queue1.isEmpty() && this.queue2.isEmpty();
    }
}

思路二：一个栈

class MyStack {
    Queue<Integer> queue;

    public MyStack() {
        this.queue = new LinkedList<>();
    }
    
    public void push(int x) {
        int size = this.queue.size();
        this.queue.offer(x);
        for (int i = 0; i < size; i++) {
            int val = this.queue.poll();
            this.queue.offer(val);//所有旧元素重新入队，使新元素位于队头
        }
    }
    
    public int pop() {
        if (empty()) return -1;
        return this.queue.poll();//队头为新元素（后进），所以栈顶元素即为队头元素
    }
    
    public int top() {
        if (empty()) return -1;
        return this.queue.peek();//队头为新元素（后进），所以栈顶元素即为队头元素
    }
    
    public boolean empty() {
        return this.queue.isEmpty();
    }
}

在线练习链接：
225. 用队列实现栈

2.3.3实现循环队列

文章前面已经介绍了循环队列的实现方式，采用顺序表，以循环的形式实现队列，判定队列是否满，是否为空有3种方式，不知道你还记得吗？

• [x] 方式1：记录队列元素个数size，当size的值与顺序表的大小相等时，代表队列已满。size值为0表示队列为空。
• [x] 方式2：使用一个boolean类型的成员变量flag标记，初始为false，当每次入队时将flag设置为true，出队将flag设置为false，当rear == front && flag == true表示队列已满，当rear == front && flag == false表示队列为空。
• [x] 方式3：牺牲一个单位的空间，在每次入队前判断（rear+1）% len是否与front相等，如果相等表示队列已满，如果rear == front则表示队列为空。

题目：实现循环队列

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。
你的实现应该支持如下操作：
MyCircularQueue(k): 构造器，设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。

示例：

MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1);  // 返回 true
circularQueue.enQueue(2);  // 返回 true
circularQueue.enQueue(3);  // 返回 true
circularQueue.enQueue(4);  // 返回 false，队列已满
circularQueue.Rear();  // 返回 3
circularQueue.isFull();  // 返回 true
circularQueue.deQueue();  // 返回 true
circularQueue.enQueue(4);  // 返回 true
circularQueue.Rear();  // 返回 4

提示：

所有的值都在 $0$ 至 $1000$ 的范围内；
操作数将在 $1$ 至 $1000$ 的范围内；
请不要使用内置的队列库。

💡解题思路：
这道题我按照方式1创建循环队列，大小为8，如图，size=0为空队列，size=8为满队列。



第一步，按照题目要求，根据传入的参数k创建顺序表大小。
第二步，记录队列元素个数size，当size的值与顺序表的大小相等时，代表队列已满。size值为0表示队列为空。
第三步，确定下标怎么变化，不妨记顺序表长度为len，下标是由0~n-1,n-1~0进行变化，所以进行下标前移时rear = (rear+1)%len，front同理。

🔑源代码：

class MyCircularQueue {
    private int[] elem;
    private int rear;//队尾
    private int front;//对头
    private int size;//有效元素个数

    public MyCircularQueue(int k) {
        this.elem = new int[k];
    }
    
    public boolean enQueue(int value) {
        if (this.size == this.elem.length) return false;
        this.elem[this.rear] = value;
        this.rear = (this.rear+1) % this.elem.length;
        size++;
        return true;
    }
    
    public boolean deQueue() {
        if (this.size == 0) return false;
        this.front = (this.front + 1) % this.elem.length;
        size--;
        return true;
    }
    
    public int Front() {
        if (isEmpty()) return -1;
        return this.elem[this.front];
    }
    
    public int Rear() {
        if (isEmpty()) return -1;
        if (this.rear == 0) {
            return this.elem[this.elem.length - 1];
        }
        return this.elem[this.rear - 1];

    }
    
    public boolean isEmpty() {
        return this.size == 0;
    }
    
    public boolean isFull() {
        return this.size == this.elem.length;
    }
}

在线练习链接：
622. 设计循环队列
好了，本文就分享到这里了，下次再见！