Java程序的封装——Java方法重载及递归
⭐️前面的话⭐️
本篇文章带大家认识Java方法,介绍Java方法之前我提一下函数,在数学中我相信大家一定都认识什么是函数,比如正反比例函数,二次函数,幂函数,指数函数,三角函数等等。
函数在数学上的定义:给定一个非空的数集A,对A施加对应法则f,记作f(A),得到另一数集B,也就是B=f(A).那么这个关系式就叫函数关系式,简称函数.
简单来讲,对于两个变量x和y,如果每给定x的一个值,y都有唯一一个确定的值与其对应,那么我们就说y是x的函数。其中,x叫做自变量,y叫做因变量。
而对于编程而言,此函数非彼函数,就拿C语言来说,函数是一段可以重复使用的代码,用来独立地完成某个功能,它可以接收用户传递的数据,也可以不接收。接收用户数据的函数在定义时要指明参数,不接收用户数据的不需要指明,根据这一点可以将函数分为有参函数和无参函数。
将代码段封装成函数的过程叫做函数定义。
Java中所谓的方法就是其他编程语言的“函数”,都是将一个实现单一的功能的代码封装。
📒博客主页:未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创!
📆华为云首发时间:🌴2022年5月31日🌴
✉️坚持和努力一定能换来诗与远方!
💭参考书籍:📚《Java核心技术卷1》,📚《Java核心技术卷2》,📚《Java编程思想》
💬参考在线编程网站:🌐牛客网🌐力扣
博主的码云gitee,平常博主写的程序代码都在里面。
博主的github,平常博主写的程序代码都在里面。
🍭作者水平很有限,如果发现错误,一定要及时告知作者哦!感谢感谢!
🍨1.Java方法基本构造
🍦1.1Java方法是什么?
在许多编程语言(比如 C 和 C++)中,“函数”用于表示子程序。而在 Java 中,我们称之为“方法”,意思是“做某件事的方式”。
Java 中的方法决定了对象可以接受哪些消息。方法最基础的几个部分包括:方法名、参数、返回值,以及方法体。
🍁使用方法有以下的优点:
- 是能够模块化的组织代码(当代码规模比较复杂的时候).
- 做到代码被重复使用, 一份代码可以在多个位置使用.
- 让代码更好理解更简单.
- 直接调用现有方法开发, 不必重复造轮子.
🍁我们要带着问题去学习,现在我给你一段判断一个数是否是素数的代码,让你改造成一个方法判断一个数是否是素数,返回值类型要求是boolean。
public static void main(String[] args) {
// 判定一个数字是否是素数
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int a = sc.nextInt();
if (a == 2) {
System.out.println(a + "是素数!");//true
continue;
}
boolean flag = true;
if (a % 2 == 0 || a <= 1) {
System.out.println(a + "不是素数!");//false
}else {
for (int i = 2; i <= Math.sqrt(a); i++) {
if (a % i == 0) {
System.out.println(a + "不是素数!");//false
flag = false;
break;
}
}
if (flag) {
System.out.println(a + "是素数!");//true
}
}
}
}
🍦1.2Java方法的定义
ReturnType methodName( /* 参数列表 */ ) {
// 方法体
}
现在我们不讨论public,private,static,我们定义方法就像main方法一样去定义:
//定义方法
public static 方法返回值 方法名称([参数类型 形参 ...]){
方法体代码;
[return 返回值];
}
//如
public static boolean isPrime(int a) {
//方法体
}
//调用
返回值变量 = 方法名称(实参...);
boolean ret = isPrime(13);
🍁注意:
- public 和 static 两个关键字在此处具有特定含义, 我们暂时不讨论, 后续博文会详细介绍.
- 方法定义时, 参数可以没有,每个参数要指定类型.
- 方法定义时, 返回值也可以没有, 如果没有返回值, 则返回值类型应写成 void.
- 方法定义时的参数称为 “形参”, 方法调用时的参数称为 “实参”.
- 方法的定义必须在类之中, 代码书写在调用位置的上方或者下方均可.
- Java 中没有 “函数声明” 这样的概念.
我们会进行方法的定义后,我们就能写出判断素数方法的外壳了!做好了外壳,就差内部的方法体了,方法体的内容就是对素数判断实现的内容。
🍦1.3Java方法的执行过程与参数
🍁基本规则🍁
- 定义方法的时候, 不会执行方法的代码. 只有调用的时候才会执行.
- 当方法被调用的时候, 会将实参赋值给形参.
- 参数传递完毕后, 就会执行到方法体代码.
- 当方法执行完毕之后(遇到 return 语句), 就执行完毕, 回到方法调用位置继续往下执行.
- 一个方法可以被多次调用.

对于基础类型来说, 形参相当于实参的拷贝. 即 传值调用。
🍁举个栗子,在一个方法中进行两数交换是无效的,因为交换的两个数实际上是形参的交换,调用完函数后形参就被销毁了,并且实参并没有进行交换,如果需要交换两数,可以采用数组,数组将在后续博文详细介绍。
🍦1.4完成判断素数的函数
前面已经介绍了方法的定义与使用,现在我们就可以完成改造,将前面给出的判断素数代码封装,实现一个判断素数的方法。
public static boolean isPrime(int a) {
//判定一个数字是否是素数方法
if (a == 2) {
return true;
}
if (a % 2 == 0 || a <= 1) {
return false;
} else {
for (int i = 2; i <= Math.sqrt(a); i++) {
if (a % i == 0) {
return false;
}
}
return true;
}
}
我们来测试一下,使用该方法试着打印1-100内的素数,我没记错的话1-100间素数个数为25个!
public static void main(String[] args) {
//打印 1 - 100 之间所有的素数
int n = 100;
int cnt = 0;
for (int i = 1; i <= n ; i++) {
if (isPrime(i)) {
cnt++;
System.out.print(i + " ");
}
}
System.out.println("1-" + n + "素数有" + cnt + "个");
}

🍨2.Java方法的重载
public class testBlog {
public static int add(int a, int b) {
return a + b;
}
public static double add(double a, double b) {
return a + b;
}
public static long add(long a, long b) {
return a + b;
}
public static void main(String[] args) {
//方法的重载
System.out.println(Integer.MAX_VALUE);//整型最大值
System.out.println(add(2, 6));//整型相加
System.out.println(add(3.14, 2.86));//浮点数相加
System.out.println(add(2147483648L,2147483649L));//长整型相加
}
}
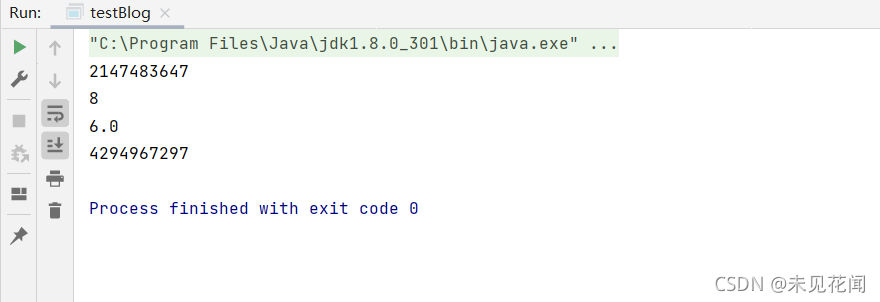
这种特征叫做重载( overloading。) 如果多个方法有相同的名字、 不同的参数,便产生了重载。编译器必须挑选出具体执行哪个方法,它通过用各个方法给出的参数类型与特定方法调用所使用的值类型进行匹配来挑选出相应的方法。如果编译器找不到匹配的参数, 就会产生编译时错误,因为根本不存在匹配, 或者没有一个比其他的更好。这个过程被称为重载解析(overloading resolution)。
🍁重载规则:
- 方法名相同
- 方法的参数不同(参数个数或者参数类型)
- 方法的返回值类型不影响重载.
🍨3.Java方法的递归
一个方法在执行过程中调用自身, 就称为 “递归”.
递归相当于数学上的 “数学归纳法”, 有一个起始条件, 然后有一个递推公式.
🍁例如, 我们求 N!
起始条件: N = 1 的时候, N! 为 1. 这个起始条件相当于递归的结束条件.
递归公式: 求 N! , 直接不好求, 可以把问题转换成 N! => N * (N-1)!

public class testBlog {
public static int factorial(int n) {
if (n == 1) {
return 1;
}
return n * factorial(n - 1);
}
public static void main(String[] args) {
//递归,n的阶乘
System.out.println(factorial(5));
}
}
测试一下,5!= 120,看看对不对。

🍦3.1斐波拉契数列
斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
特别指出:第0项是0,第1项是第一个1。这个数列从第3项开始,每一项都等于前两项之和。
🍁斐波拉契数列的通项公式为:F(N) = F(N - 1) + F(N -2)
🍁起始条件:N = 0,F(0) = 0; N = 1,F(1) = 1;
🍁递归实现:
public class testBlog {
public static int fib1(int n) {
if (n == 0 || n == 1) {
return n;
}
return fib1(n - 1) + fib1(n - 2);
}
public static void main(String[] args) {
//斐波拉契数列
for (int i = 0; i < 13; i++) {
System.out.print(fib1(i) + " ");
}
}
}
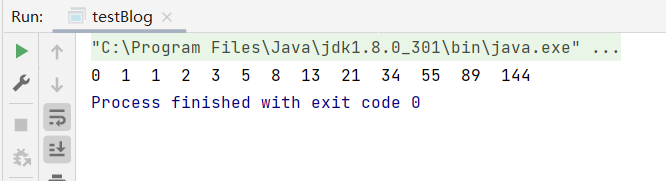
但是使用递归实现斐波拉契数列,求后面的项会变得越来越慢,因为会进行大量重复的项的计算。
🍁推荐使用迭代的方法实现:
public class testBlog {
//fib1递归,fib2迭代
public static int fib1(int n) {
if (n == 0 || n == 1) {
return n;
}
return fib1(n - 1) + fib1(n - 2);
}
public static int fib2(int n) {
if (n == 0 || n == 1) {
return n;
}
int f0 = 0;
int f1 = 1;
int fn = 0;
while (n - 1 != 0) {
fn = f0 + f1;
f0 = f1;
f1 = fn;
n--;
}
return fn;
}
public static void main(String[] args) {
//斐波拉契数列
for (int i = 0; i < 13; i++) {
System.out.print(fib1(i) + " ");//递归结果
}
System.out.println();
for (int i = 0; i < 13; i++) {
System.out.print(fib2(i) + " ");//迭代结果
}
}
}

🍦3.2青蛙跳台阶问题
🍧3.2.1题目描述及思路
🍁题目:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法?
解题思路
1.当n=1的时,很明显青蛙只有一种跳法。
2.当n=2时,青蛙有两种选择,一是每次跳1级台阶,跳两次,二是直接跳两级台阶,一步到位。所以,一共有两种跳法。
3.当n>2时,我们不妨把上n级台阶的跳法记为一个函数f(n),青蛙在第一次跳的时候有两个选择,即跳一级台阶或跳两级台阶。当青蛙选择第一次跳一级台阶时,跳完后还剩n-1级台阶,在此情况下,跳法的数目为f(n-1);当青蛙选择第一次跳两级台阶时,跳完后还剩n-2级台阶,在此情况下,跳法数目为f(n-2)。所以,我们可以推出青蛙跳n级台阶的跳法总数为f(n)=f(n-1)+f(n-2)。
到这里我们就能使用求斐波拉契数列的方法来求青蛙跳n级台阶的跳法。
🍁若把条件修改成一次可以跳一级,也可以跳2级…也可以跳上n级呢?
解题思路
尽管条件改成每次跳的台阶级数不受限,但是换汤不换药,思考的方法是一样的。
1.当n=1或n=2时,青蛙跳台阶跳法次数和没修改条件时是一样的,n=1有一种跳法,n=2有两种跳法。
2.当n>2时,同理我们将青蛙跳n级台阶时的跳法记成函数f(n)。但是青蛙在第一次的选择不仅仅是跳1级和跳2级,它还可以选择跳3,4,5,…,n级。所以青蛙跳一次后还会剩n-1,n-2,n-3,…,2, 1, 0级台阶。
此时,f(n)=f(n-1)+f(n-2)+f(n-3)+…+f(2)+f(1)+1
同理,f(n-1)=f(n-2)+f(n-3)+f(n-4)+…+f(2)+f(1)+1
合并上面两个式子得,f(n)=2*f(n-1)
3.根据2的推论得出一个等比数列,由此我们还可以进一步推导:
🍁推导1:f(n)=f(n-1)+f(n-2)+f(n-3)+…+f(2)+f(1)+1
=1+f(1)+f(2)+…+f(n-2)+f(n-1)
=1+2^0^*f(1)+2^1^*f(1)+…+2^n-3^*f(1)+2^n-2^*f(1)
=1+(2^0^+2^1^+2^2^+…+2^n-3^+2^n-2^)
=1+(2^n-1^-1)
=2^n-1^
f(1) = 1,f(2) = 2,f(n)为公比的2的等比数列(n>2)
🍁推导2:f(1) = 2^0^, f(2) = 2^1^, f(3) = 2^2^…, f(n-1) = 2^n-2^, f(n) = 2^n-1^
🍧3.2.2代码演示
public class testBlog {
//frog1递归,frog2迭代
public static int frog1(int n) {
if (n <= 2) {
return n;
}
return frog1(n - 1) + frog1(n - 2);
}
public static int frog2(int n) {
if (n == 1 || n == 2) {
return n;
}
int f1 = 1;
int f2 = 2;
int fn = 0;
while (n - 2 != 0) {
fn = f1 + f2;
f1 = f2;
f2 = fn;
n--;
}
return fn;
}
public static int frogPlus1(int n) {
if (n == 1) {
return n;
}
return 2 * frogPlus1(n - 1);
}
public static int frogPlus2(int n) {
if (n == 1) {
return n;
}
int f1 = 1;
int fn = 0;
while (n - 1 != 0) {
fn = 2 * f1;
f1 = fn;
n--;
}
return fn;
}
public static int frogPlus3(int n) {
return (int)Math.pow(2, n - 1);
}
public static void main(String[] args) {
//青蛙跳台阶
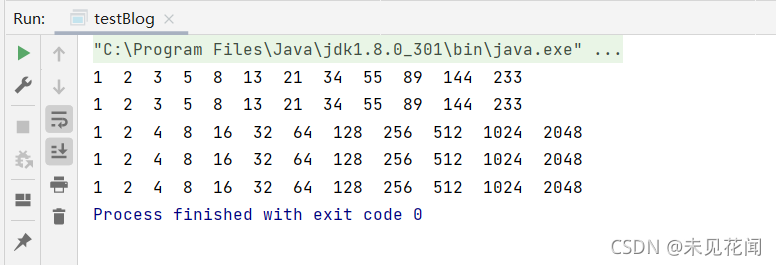
for (int i = 1; i < 13; i++) {
System.out.print(frog1(i) + " ");//青蛙跳台阶递归结果
}
System.out.println();
for (int i = 1; i < 13; i++) {
System.out.print(frog2(i) + " ");//青蛙跳台阶迭代结果
}
System.out.println();
for (int i = 1; i < 13; i++) {
System.out.print(frogPlus1(i) + " ");//青蛙跳台阶变式递归结果
}
System.out.println();
for (int i = 1; i < 13; i++) {
System.out.print(frogPlus2(i) + " ");//青蛙跳台阶变式迭代结果
}
System.out.println();
for (int i = 1; i < 13; i++) {
System.out.print(frogPlus3(i) + " ");//青蛙跳台阶变式结论结果
}
}
}
🍦3.3汉诺塔问题
🍧3.3.1问题描述及思路
Hanoi(汉诺)塔问题。古代有一个梵塔,塔内有3个座A,B,C。开始时A座上有64个盘子,盘子大小不等,大的在下,小的在上。有一个先知想把这64个盘子从A座移到C座,但规定每次只允许移动一个盘,且在移动过程中在3个座上都始终保持大盘在下,小盘在上。在移动过程中可以利用B座。你能帮这位先知实现他的想法吗?要求编程序输出移动盘子的步骤。
🍁解题思路:
这位先知会这样想: 假如有另外一位先知能有办法将上面63个盘子从A座移到B座。那么,问题就解决了。此时先知只须这样做:
① 联系他的好朋友第2个先知将63个盘子从A座移到B座;
② 自己将1个盘子(最底下的、最大的盘子)从A座移到C座;
③ 再让第2个先知将63个盘子从B座移到C座。
第2个先知又想: 如果有人能将62个盘子从一个座移到另一座,我就能将63个盘子从A座移到B座,他是这样做的:
① 联系他的好朋友第3个先知将62个盘子从A座移到C座;
② 自己将1个盘子从A座移到B座;
③ 再让第3个先知将62个盘子从C座移到B座。
……
以此类推

为了便于理解,我们将盘子数量降低到3个,所以首先分析将A座上3个盘子移到C座上的过程:
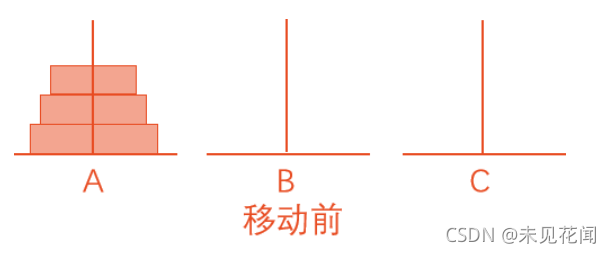
① 将A座上2个盘子移到B座上(借助C座)。
② 将A座上1个盘子移到C座上。
③ 将B座上2个盘子移到C座上(借助A座)。

其中第②步可以直接实现。第①步又可用递归方法分解为:
- 将A座上1个盘子从A座移到C座;
- 将A座上1个盘子从A座移到B座;
- 将C座上1个盘子从C座移到B座。
第③步可以分解为:
- 将B座上1个盘子从B座移到A座上;
- 将B座上1个盘子从B座移到C座上;
- 将A座上1个盘子从A座移到C座上。
将以上综合起来,可得到移动3个盘子的步骤为:
A→C,A→B,C→B,A→C,B→A,B→C,A→C。
共经历7步。由此可推出: 移动n个盘子要经历(2^n^-1)步。
🍧3.3.2代码演示
🍁由上面的分析可知: 将n个盘子从A座移到C座可以分解为以下3个步骤:
① 将A座上n-1个盘借助C座先移到B座上;
② 把A座上剩下的一个盘移到C座上;
③ 将n-1个盘从B座借助于A座移到C座上。
🍁可以把上面3个步骤分成两类操作:
① 将n-1个盘从一个座移到另一个座上(n>1)。这就是先知让他的朋友第2个先知做的工作,它是一个递归的过程,即先知将任务层层下放,直到第64个先知为止。——hanoi函数
② 将1个盘子从一个座上移到另一座上。这是先知自己做的工作。——move函数
public class testBlog {
public static void move(char m, char n) {
System.out.println(m + "->" + n);
}
public static void hanoi(int num, char a, char b, char c) {
if (num == 1) {
move(a, c);
return;
}
hanoi(num - 1, a, c, b);
move(a, c);
hanoi(num - 1, b, a, c);
}
public static void main(String[] args) {
//Hanoi(汉诺)塔问题。古代有一个梵塔,塔内有3个座A,B,C。
//开始时A座上有64个盘子,盘子大小不等,大的在下,小的在上。
//有一个先知想把这64个盘子从A座移到C座,但规定每次只允许移动一个盘,
//且在移动过程中在3个座上都始终保持大盘在下,小盘在上。
//在移动过程中可以利用B座。你能帮这位先知实现他的想法吗?
//要求编程序输出移动盘子的步骤。
int num = 3;
hanoi(3,'A', 'B', 'C');
}
}
看看3个盘子的汉诺塔程序是怎么移动的:
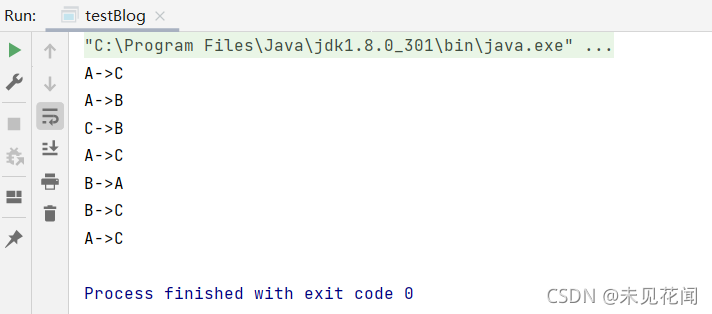
与我们推演出来的移动顺序一致!
- 点赞
- 收藏
- 关注作者


评论(0)