【优化算法】迭代扩展卡尔曼滤波算法（IEKF）【含Matlab源码 1584期】
【摘要】
一、获取代码方式
获取代码方式1： 通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。
获取代码方式2： 完整代码已上传我的资源：【优化算法】迭代扩展卡尔曼滤波算法（IEKF）【含Ma...
一、获取代码方式
获取代码方式1：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。
获取代码方式2：
完整代码已上传我的资源：【优化算法】迭代扩展卡尔曼滤波算法（IEKF）【含Matlab源码 1584期】
备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；
二、迭代扩展卡尔曼滤波算法（IEKF）简介
IEKF与EKF的不同之处主要在于测量更新过程，对于IEKF, 在得到状态预测
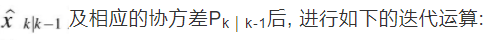
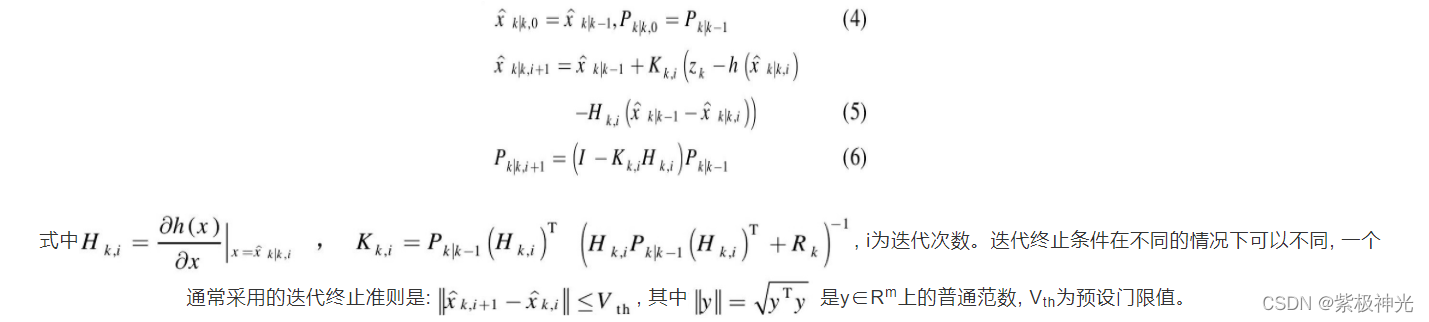
文献[8]证明了IEKF迭代结果与高斯牛顿方法估计的结果是一致的, 因此IEKF可以保证全局收敛。理论上, IEKF优于EKF和MVEKF, 然而, 实际中并不完全如此, 因为: (1) 文献[8]给出的结论是建立在必须满足局部线性化条件的假设之上, 也就是说, 状态估计必须足够接近于真实值, 这在很多应用中不是总能成立, 因为初始估计误差可能会很大。 (2) 高斯牛顿方法虽然能保证全局收敛, 但不能保证达到似然面[9]。另外, 预设门限Vth对迭代过程很关键, 要选择一个合适的值不容易。
为此, 对IEKF进行修正。为方便起见, 把当前观测与状态估计合并为一个“观测”向量, 因此, 得到扩展的观测量与测量方程:
三、部分源代码
% function to implement the Iterated Extended Kalman Filter (IEKF)
% Inputs:
% OBSn - the observations (with noise)
% xest - initial state space estimates
% Ouputs:
% Xp - predicted states
function Xp = f_IEKF(OBSn,xest)
load avar % r1,r2, L, and T
tol = .1; % tolerance for iterations
diff = 1;
count = 0;
F = [1 T 0 0 0 0 0;
0 1 0 0 0 0 0;
0 0 1 T 0 0 0;
0 0 0 1 0 0 0;
0 0 0 0 1 0 T;
0 0 0 0 0 1 T;
0 0 0 0 0 0 1]; % state transition matrix
n = size(OBSn,2); % number of observations
Xp = zeros(7,n); % make room
Pkp1 = 1e10*eye(7); %xest*xest'; %.1*ones(7,7);
%Pkp1 = xest*xest';
%Pkp1 = F*Pkp1*F';
%Pkp1 = (10*randn(7,1))*(10*randn(7,1)).';
%Pkp1 = F*Pkp1*F';
% for each observation
for i = 1:n;
% if this is the first iteration the prior predicted estimate is xest
% if this is not the first run the prior estimate is in Xp
if i == 1
xkm1 = xest;
else
xkm1 = Xp(:,i-1);
end
Pkm1 = Pkp1; % conditional covariance from last iteration
% iterations are started with the predicted estimate from the last run
xkn = xkm1;
while ~(diff < tol || count > 9)
count = count + 1;
H = [gradest(@(x)f_h1(x),xkn); gradest(@(x)f_h2(x),xkn)];
R = (.01*randn(2,1))*(.01*randn(2,1)).';
Rdiag = diag(R); R = diag(Rdiag);
K = Pkm1*H'*(H*Pkm1*H'+R)^-1;
xkn_temp = xkm1 + K*(OBSn(:,i)-f_h(xkn)-H*(xkm1-xkn));
diff = norm(abs(xkn_temp-xkn));
fprintf('diff = %g \n',diff)
xkn = xkn_temp;
end
H = [gradest(@(x)f_h1(x),xkn); gradest(@(x)f_h2(x),xkn)];
Pkk = (eye(7)-K*H)*Pkm1;
Pkp1 = F*Pkk*F';
Xp(:,i) = F*xkn;
clc;
fprintf('i = %g; Count is %g \n',i,count)
count = 0;
diff = 1;
end
% Script to start playing around with this stuff
clc; clear all; close all
% x = [xc xcd zc zcd p1 p2 w].'
% simulation parameters
n = 100; % number of frames
xint = [-35 .7 35 .4 1 3 1].'; % initial state variable
xest = [-32 .9 32 .6 1.2 2.2 .7].'; % initial state estimates
noise = .01;
% simulate dynamics
X = f_Simulate(xint,n);
% simulate observations
[OBS, OBSn] = f_Observe(X,noise);
% make movie
f_Movie(X,OBS,'SimMovie')
% run filter
Xp = f_IEKF(OBSn,xest);
% make movie
OBSr = f_Observe(Xp,0);
f_Movie(Xp,OBSr,'ResultsMovie')
save RunData
% pixel values
figure;
pos = get(gcf,'Position');
set(gcf,'Position',[pos(1)-100 pos(2)-200 1.5*pos(3) 1.5*pos(4)]);
plot(1:n,OBSn,'.-',1:n,OBSr,'.-'); grid on;
legend('X1 simulated','X2 simulated','X1 predicted','X2 predicted','Location','Best')
xlabel('Frame index (n)','FontName','Time','FontSize',15);
ylabel('Image pixel value','FontName','Time','FontSize',15);
title('Pixel observations with noise',...
'FontName','Time','FontSize',15,'FontWeight','Bold');
Error = X - Xp;
% error (xc and zc)
figure;
pos = get(gcf,'Position');
set(gcf,'Position',[pos(1)-100 pos(2)-200 1.5*pos(3) 1.5*pos(4)]);
plot(1:n,Error([1 3],:),'.-'); grid on;
legend('xc','zc','Location','Best')
xlabel('Frame index (n)','FontName','Time','FontSize',15);
ylabel('Error','FontName','Time','FontSize',15);
title('Error in xc and zc',...
'FontName','Time','FontSize',15,'FontWeight','Bold');
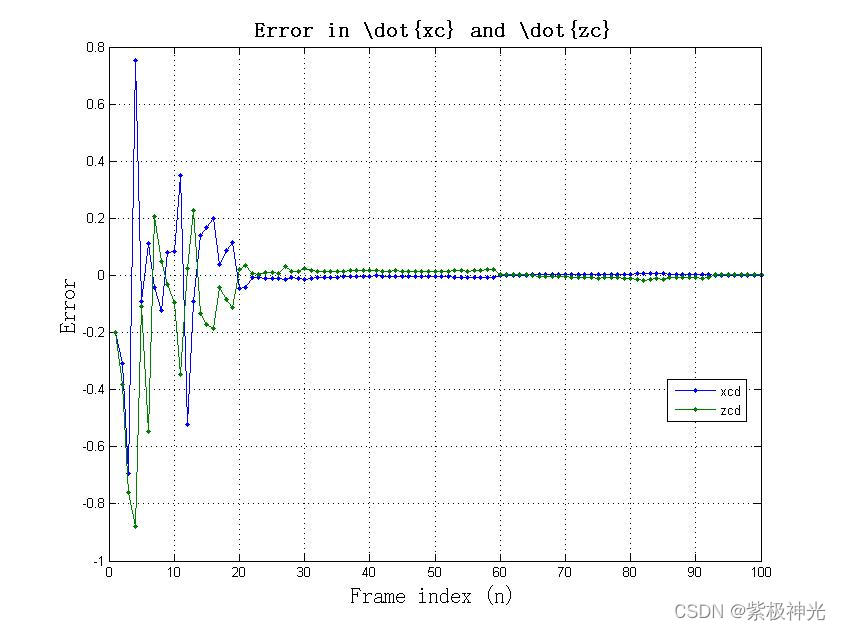
% error (xcd and zcd)
figure;
pos = get(gcf,'Position');
set(gcf,'Position',[pos(1)-100 pos(2)-200 1.5*pos(3) 1.5*pos(4)]);
plot(1:n,Error([2 4],:),'.-'); grid on;
legend('xcd','zcd','Location','Best')
xlabel('Frame index (n)','FontName','Time','FontSize',15);
ylabel('Error','FontName','Time','FontSize',15);
title('Error in \dot{xc} and \dot{zc}',...
'FontName','Time','FontSize',15,'FontWeight','Bold');
% error (p1 w)
figure;
pos = get(gcf,'Position');
set(gcf,'Position',[pos(1)-100 pos(2)-200 1.5*pos(3) 1.5*pos(4)]);
plot(1:n,Error([5 7],:),'.-'); grid on;
legend('p1','w','Location','Best')
xlabel('Frame index (n)','FontName','Time','FontSize',15);
ylabel('Error','FontName','Time','FontSize',15);
title('Error in p1 and w',...
'FontName','Time','FontSize',15,'FontWeight','Bold');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
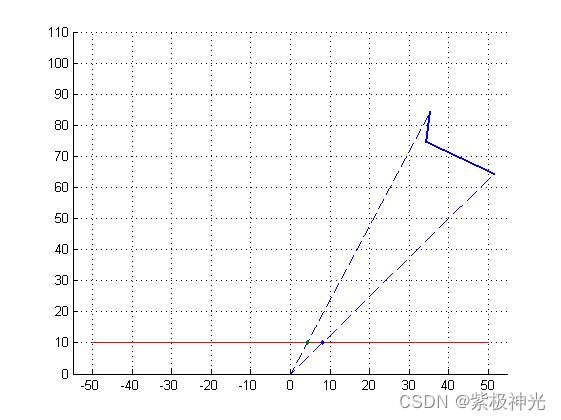
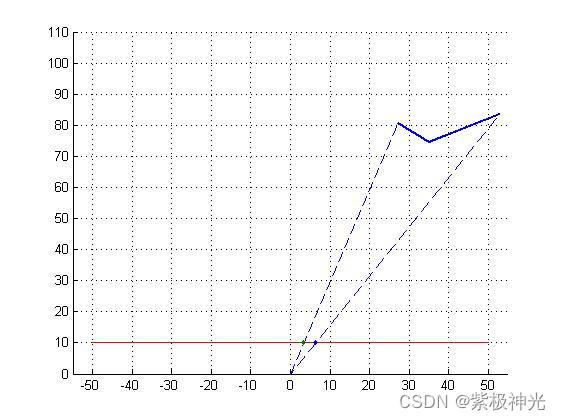
四、运行结果
五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]张俊根,姬红兵.IMM迭代扩展卡尔曼粒子滤波跟踪算法[J].电子与信息学报. 2010,32(05)
文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。
原文链接：qq912100926.blog.csdn.net/article/details/121884197
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）