【单目标优化求解】基于matlab多子群改进的海洋捕食者算法(MSMPA)求解单目标优化问题【含Matlab源码 1783期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【单目标优化求解】基于matlab多子群改进的海洋捕食者算法(MSMPA)求解单目标优化问题【含Matlab源码 1783期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、海洋捕食者算法（MPA）简介

1 海洋捕食者算法（MPA）定义
海洋捕食者算法(MPA)是一种自然启发式的优化算法,它遵循在最佳觅食策略中自然支配的规则,并且在海洋生态系统中遇到捕食者与猎物之间的速率策略。

2 海洋捕食者算法（MPA）流程
(1) 初始化精英矩阵(Elite)和猎物矩阵(Prey)
猎物矩阵(Prey) 矩阵每一个元素 Xij 的初始化方法:

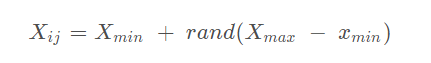
最终得到的Prey矩阵:

其中，n是种群的规模，d是每个维度的位置(问题的解的维度)。
对每一个Prey个体Xi = [Xi,1, Xi,2, …, Xi,d], 计算其适应度, 然后使用适应度最优的个体 XI 复制n份构成Elite矩阵

其中n是种群的规模，d是每个维度的位置(问题的解的维度)，Elite的维度与Prey的维度相同。
(2)接着我们开始进行优化。在优化的过程中，具有三个步骤。
步骤一:
当迭代次数小于最大迭代次数的三分之一的时候

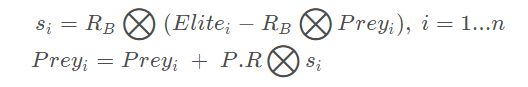
其中，RB 是采用布朗随机游走产生的随机数组成的向量，维度是 d(问题的求解规模，下同)。si 代表移动的步长。 P是一个常数，等于0.5。R是一个0到1之间的均匀分布的随机数组成的向量，维度是 d。
RB相当于一般化的高斯分布(Normal Gaussian distribution)。每一个元素 RBi 可以通过下列表达式来计算:

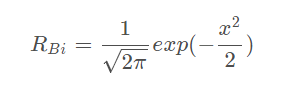
步骤二:
当迭代次数大于最大迭代次数的三分之一而小于其三分之二时，种群分两部分进行操作。
前半部分种群跟新规则如下：

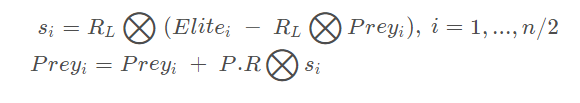
其中， RL 是 Levy 分布组成的出来的一个向量，维度是 d。P是一个常数，等于0.5。R是一个0到1之间的均匀分布的随机数组成的向量，维度是 d。
RL 的每一项元素 RLi 可以由下列式子计算得来:

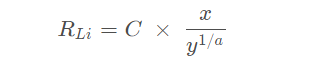
其中，C 和 α是一个常数，分别等于0.05和1.5。

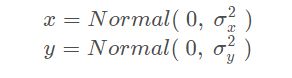
在上面的表达式中

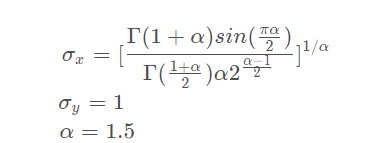
后半部分种群跟新规则如下:

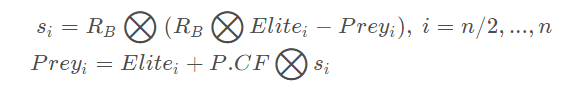
这里RB 是采用布朗随机游走产生的随机数组成的向量，维度是 d。P是常数，等于0.5。CF是步长si 的自适应参数(下同), 定义为

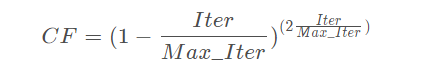
其中, Iter是迭代次数，Max_Iter是最大迭代次数。
步骤三：
当迭代次数大于最大迭代次数的三分之二时，进入第三个阶段，此时种群更新规则如下:

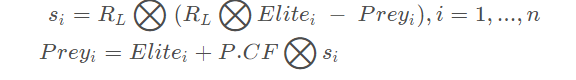
(3) 解决涡流形成和FADS效应(Eddy formation and FADs’ effect)
此操作的作用是让算法在迭代过程中尽可能跳出局部最优解，已达到更好的寻优精度。

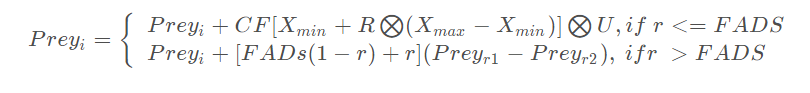
其中r是一个随机数, FADS是一个影响优化过程的常数，等于0.2。r1和r2是Prey两个随机下标, 1 ≤ r1,r2 ≤ n。 U是一个包含0和1的二进制向量，维度是d。U的每一个元素 Ui 定义为

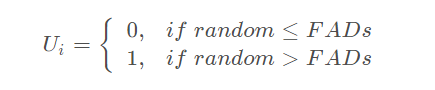
其中random是一个0到1的随机数，FADs等于0.2。
(4) 海洋记忆(Marine memory)
这一步骤进行对Elite(精英)矩阵的更新。
针对每一个Prey矩阵中的个体Preyi ,计算其适应度，若适应度由于Elite矩阵矩阵中相应的位置的适应度时，则将该个体替代原来精英矩阵中相应的个体。然后在计算整个精英矩阵中最优个体的适应度，若符合要求，则算法结束，否则继续迭代。
算法的流程图总结出来如下:

三、部分源代码

clear all
clc
SearchAgents_no=30; % Number of search agents

Function_name='F1';
   
Max_iteration=500; % Maximum number of iterations

[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
%原始海洋捕食者算法
[Best_score,Best_pos,Convergence_curve]=MPA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
%改进海洋捕食者算法
[Best_score1,Best_pos1,Convergence_curve1]=MSMPA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);

% function topology
figure('Position',[500 400 700 290])
subplot(1,2,1);
func_plot(Function_name);
title('Function Topology')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])

% Convergence curve
subplot(1,2,2);
semilogy(Convergence_curve,'Color','b','linewidth',1.5);
hold on;
semilogy(Convergence_curve1,'Color','r','linewidth',1.5);
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
grid on;
legend('MSA','MSMSA')

display(['The best solution obtained by MPA is : ', num2str(Best_pos,10)]);
display(['The best optimal value of the objective function found by MPA is : ', num2str(Best_score)]);


display(['The best solution obtained by MSMPA is : ', num2str(Best_pos1,10)]);
display(['The best optimal value of the objective function found by MSMPA is : ', num2str(Best_score1)]);


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
 

四、运行结果

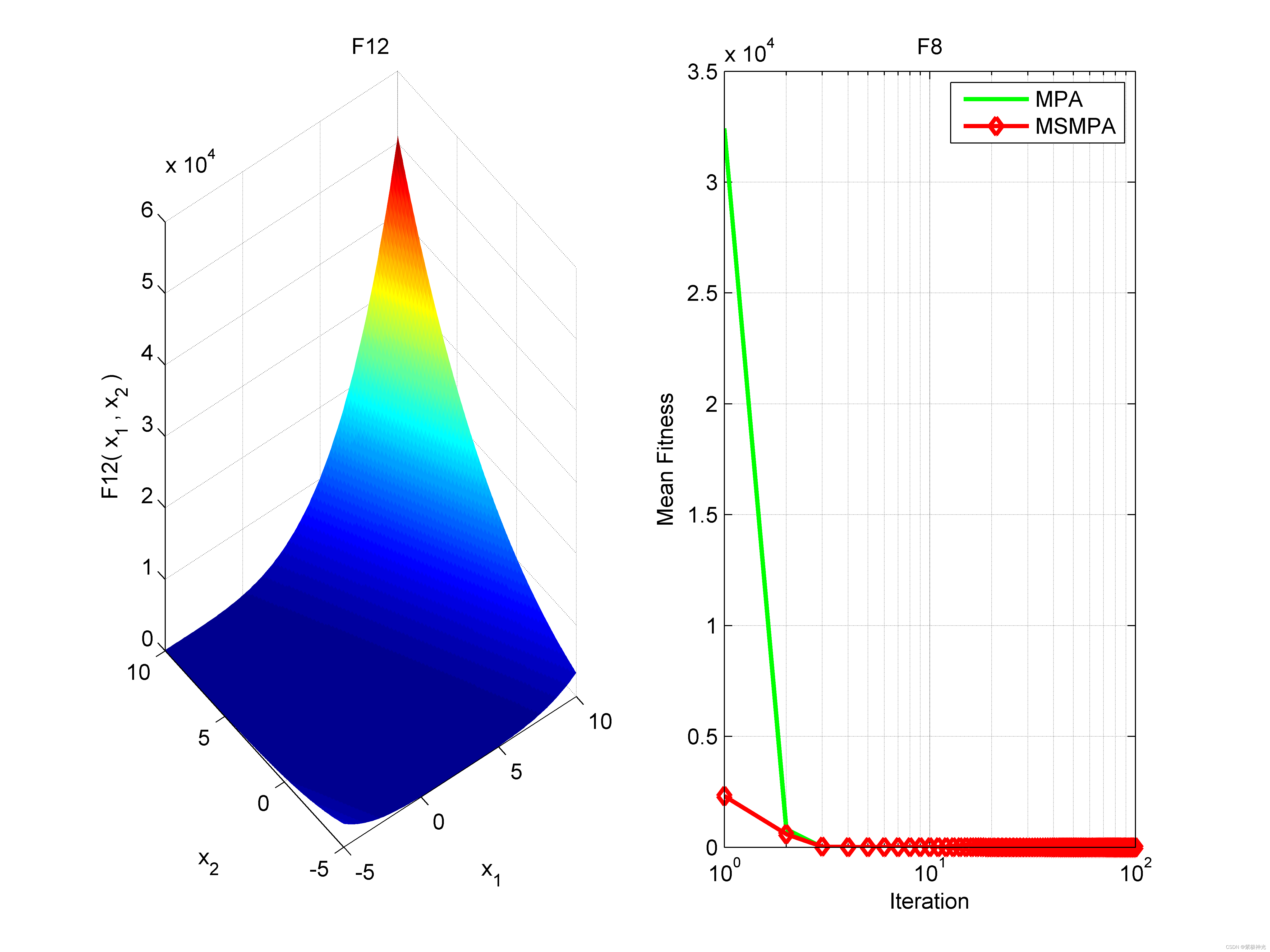
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张磊,刘升,高文欣,郭雨鑫.多子群改进的海洋捕食者算法[J/OL].微电子学与计算机:1-9[2021-11-01]

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/123513248