【LSSVM回归预测】基于matlab飞蛾扑火算法优化LSSVM回归预测【含Matlab源码 110期】

一、飞蛾扑火算法及LSSVM简介

1 飞蛾扑火算法简介
1.1 飞蛾扑火算法定义
飞蛾扑火优化(Moth-flame optimization，MFO)，由Seyedali Mirjalili在2015年提出，为优化领域提供了一种新的启发式搜索范式：螺旋搜索。
飞蛾在夜间有一种特殊的导航方式：横向定向。即它会与月亮(光源)保持一定的角度飞行，从而能够保持直线的飞行路径，但是，这种方式只在光源离飞蛾较远的情况下才有效。当有人造光源存在时，飞蛾会被人工灯光所欺骗，一直保持与人造灯光相同的角度飞行，由于它与光源的距离过近，它飞行的路径已经不是直线，而是一种螺旋的路径。

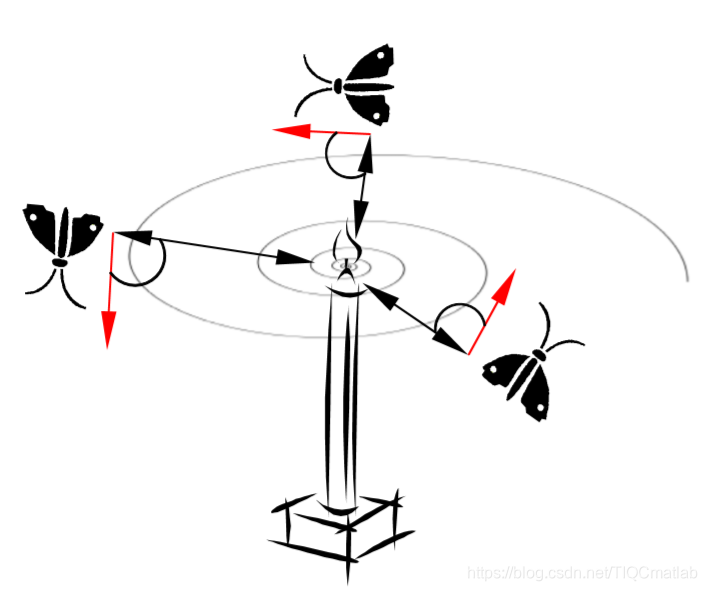
受这种自然现象的启发，Seyedali Mirjalili将飞蛾绕着光源螺旋飞行的过程抽象成为一个寻优的过程，飞蛾飞行的整个空间即是问题的解空间，一只飞蛾即是问题的一个解，而火焰(光源)即是问题的一个较优解，每一只飞蛾对应一个光源，避免了算法陷入局部最优；当飞蛾与火焰足够多的时候，飞蛾的飞行能够搜索解空间的绝大部分区域，从而保证了算法的探索能力；而在寻优的过程中，火焰数随着迭代次数的增加而减少，使飞蛾能够充分搜索更优解的邻域空间，保证了算法的利用能力。
正是基于以上特点，MFO在探索与利用之间找到了平衡，从而使算法在优化问题中有一个较好的效果。
总的来说MFO也是一种基于种群的随机启发式搜索算法，它与PSO、GSA等算法最大的区别就在于其粒子搜索路径是螺旋形的，粒子围绕着更优解以一种螺旋的方式移动，而不是直线移动。

1.2 MFO过程
1.初始化飞蛾种群
2.对飞蛾种群进行适应度评价
3.重复如下过程直到达到停止标准：
3.1自适应更新火焰个数n，当迭代次数为1时，飞蛾个数即为火焰个数
3.2对飞蛾种群适应度进行排序，取出适应度较好的n个飞蛾作为火焰
3.3更新飞蛾的搜索参数。
3.4根据每只飞蛾对应的火焰与飞行参数更新飞蛾的位置
4.输出所得最优解(火焰)

2 LSSVM简介
2.1 最小二乘支持向量机LSSVM基本原理
最小二乘支持向量机是支持向量机的一种改进，它是将传统支持向量机中的不等式约束改为等式约束, 且将误差平方和(SumSquaresError)损失函数作为训练集的经验损失,这样就把解二次规划问题转化为求解线性方程组问题, 提高求解问题的速度和收敛精度。
常用的核函数种类：

2.2 LSSVM工具箱的使用方法
2.1 最小二乘支持向量机Matlab工具箱下载链接https://www.esat.kuleuven.be/sista/lssvmlab/（毫无疑问下载最新版本）
2.2 将LS-SVM文件添加到matlan使用路径中，便可直接使用。

具体使用步骤：
（1）导入训练数据：load 读取mat文件和ASCII文件；xlsread读取.xls文件；csvread读取.csv文件。
（2）数据预处理：效果是加快训练速度。
方法有：归一化处理(把每组数据都变为 - 1～ +1之间的数, 所涉及到的函数有premnmx, post mnmx, tramnmx)
标准化处理(把每组数据都化为均值为 0, 方差为 1的一组数据, 所涉及到的函数有 prestd,poatstd, trastd)
主成分分析 (进行正交处理, 减少输入数据的维数, 所涉及到的函数有 prepca, trapca)
（3）LS-SVM lab用于函数回归主要用到 3个函数, trainlssvm函数用来训练建立模型, simlssvm函数用于预估模型, plotlssvm函数是 LS-SVM lab工具箱的专用绘图函数。
（4） 参数说明：
A =csvread(′traindata. csv′);
Ptrain0=A(:, [ 1:13] );Ttrain0=A(:, [ 14:16);
[ Ptrain, meanptrain, stdptrain] = prestd(Ptrain0′);
[ Ttrain, meant , stdt] = prestd(T train0′);
Prestd()是数据归一化函数, 其中 meanptrain是未归一化数据之前的向量平均值 stdptrain是未归一化数据之前的向量标准差。
gam =10;sig2=0. 5;type=′function estimation′;
LS-SVM 要求调的参数就两个。 gam 和 sig2是最小二乘支持向量机的参数, 其中 gam 是正则化参数, 决定了适应误差的最小化和平滑程度, sig2是 RBF 函数的参数。 在工具箱中有一个函数 gridsearch可以在一定的范围内用来寻找最优的参数范围。 type有两种类型, 一种是 classfication, 用于分类, 一种是 function estimation, 用于函数回归。
[ alpha, b] =trainlssvm({Ptrain′, Ttrain′, type, gam, sig2,′RBF_kernel′, ′preprocess′});
alpha是支持向量, b是阈值. 。 preprocess是表明数据已经进行归一化, 也可以是′original ′, 表明数据没有进行归一化, 缺省时是′preprocess′。
plotlssvm ({P, T, type, gam, sig2, ′RBF _ kernel ′,′preprocess′}, {alpha, b})plotlssvm函数是 LS-SVM 工具箱特有的绘图函数, 和 plot函数原理相近。
simlssvm函数也是 LS-SVM 工具箱的重要函数, 其中的参数如上述所示, 原理类似于神经网络工具箱中的 sim 函数。
通过调用 trainlssvm函数和 si m lssvm 函数我们可以看到最小二乘支持向量机和神经网络的结构有很多共同之处。
与神经网络进行对比：
神经网络建立的模型要比 LS-SVM 好, 但是在预估上, LS-SVM 要优于神经网络,具有较好的泛化能力, 而且训练速度要比神经网络快。

二、部分源代码

%=====================================================================
%初始化
clc
close all
clear
format long
tic
%==============================================================
%%导入数据
data=xlsread('1.xlsx');
[row,col]=size(data);
x=data(:,1:col-1);
y=data(:,col);
set=1; %设置测量样本数
row1=row-set;%
train_x=x(1:row1,:);
train_y=y(1:row1,:);
test_x=x(row1+1:row,:);%预测输入
test_y=y(row1+1:row,:);%预测输出
train_x=train_x';
train_y=train_y';
test_x=test_x';
test_y=test_y';
 
%%数据归一化
[train_x,minx,maxx, train_yy,miny,maxy] =premnmx(train_x,train_y);
test_x=tramnmx(test_x,minx,maxx);
train_x=train_x';
train_yy=train_yy';
train_y=train_y';
test_x=test_x';
test_y=test_y';
%% 参数初始化
eps = 10^(-6);
%%定义lssvm相关参数
type='f';
kernel = 'RBF_kernel';
 
N=20; % Number of search agents
Max_iteration=100; % Maximum numbef of iterations
Leader_pos=zeros(1,dim);
Leader_score=inf; %change this to -inf for maximization problems
%Initialize the positions of search agents
% for i=1:SearchAgents_no
%     Positions(i,1)=ceil(rand(1)*(ub(1)-lb(1))+lb(1));
%     Positions(i,2)=ceil(rand(1)*(ub(2)-lb(2))+lb(2));
%     
end
 
%% 结果分析
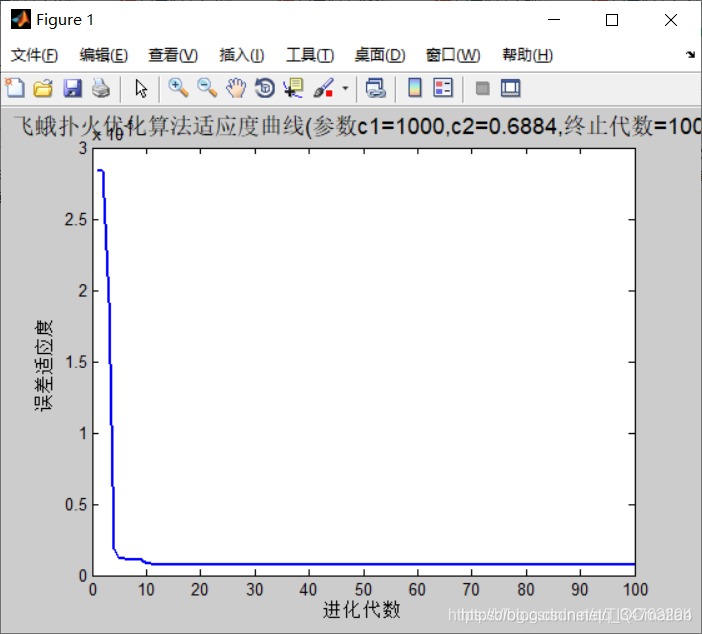
plot( Convergence_curve,'LineWidth',2);
title(['飞蛾扑火优化算法适应度曲线','(参数c1=',num2str(Best_flame_pos(1)),',c2=',num2str(Best_flame_pos(2)),',终止代数=',num2str(Max_iteration),')'],'FontSize',13);
xlabel('进化代数');ylabel('误差适应度');
 
bestc = Best_flame_pos(1);
bestg = Best_flame_pos(2);
 
gam=bestc;
sig2=bestg;
model=initlssvm(train_x,train_yy,type,gam,sig2,kernel,proprecess);%原来是显示
model=trainlssvm(model);%原来是显示
%求出训练集和测试集的预测值
[train_predict_y,zt,model]=simlssvm(model,train_x);
[test_predict_y,zt,model]=simlssvm(model,test_x);
 
%预测数据反归一化
train_predict=postmnmx(train_predict_y,miny,maxy);%预测输出
test_predict=postmnmx(test_predict_y,miny,maxy);
%计算均方差
trainmse=sum((train_predict-train_y).^2)/length(train_y);
%testmse=sum((test_predict-test_y).^2)/length(test_y)
 
for i=1:set
    RD(i)=(test_predict(i)-test_y(i))/test_y(i)*100;
end
for i=1:set
    D(i)=test_predict(i)-test_y(i);
end
RD=RD'
disp(['飞蛾扑火优化算法优化svm预测误差=',num2str(D)])
figure
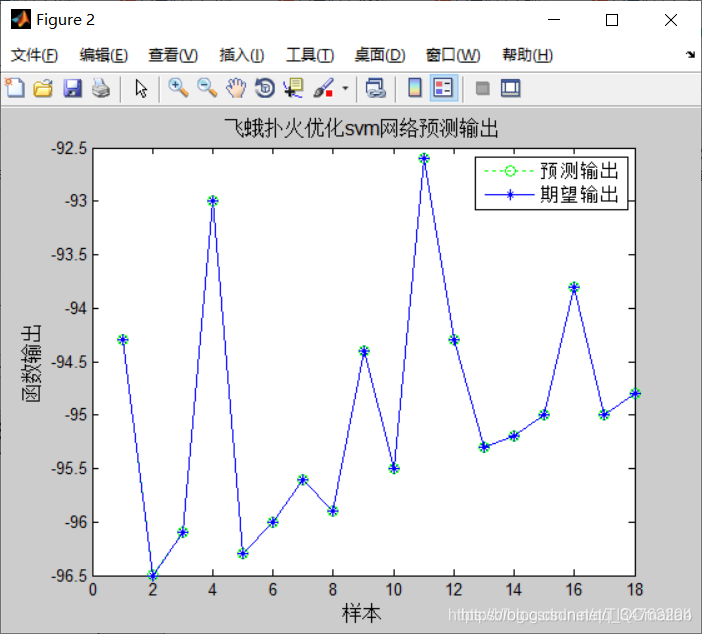
plot(train_predict,':og')
hold on
plot(train_y,'- *')
legend('预测输出','期望输出')
title('飞蛾扑火优化svm网络预测输出','fontsize',12)
ylabel('函数输出','fontsize',12)
xlabel('样本','fontsize',12)
 
toc   %计算时间
 

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/112907996