【LSSVM回归预测】基于matlab蝙蝠算法优化LSSVM回归预测【含Matlab源码 109期】

一、简介

LSSVM的特性
  1) 同样是对原始对偶问题进行求解，但是通过求解一个线性方程组（优化目标中的线性约束导致的）来代替SVM中的QP问题（简化求解过程），对于高维输入空间中的分类以及回归任务同样适用；
  2) 实质上是求解线性矩阵方程的过程，与高斯过程（Gaussian processes），正则化网络（regularization networks）和费雪判别分析（Fisher discriminant analysis）的核版本相结合；
  3) 使用了稀疏近似（用来克服使用该算法时的弊端）与稳健回归（稳健统计）；
  4) 使用了贝叶斯推断（Bayesian inference）；
  5) 可以拓展到非监督学习中：核主成分分析（kernel PCA）或密度聚类；
  6) 可以拓展到递归神经网络中。

LSSVM用于分类任务
  1) 优化目标
  
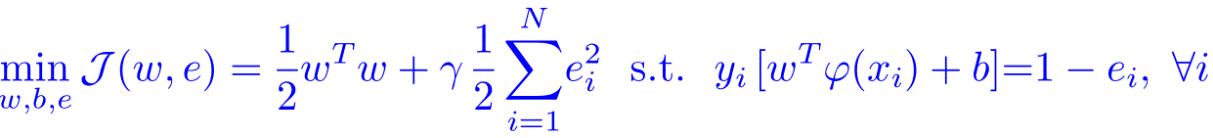
 2) 拉格朗日乘子法

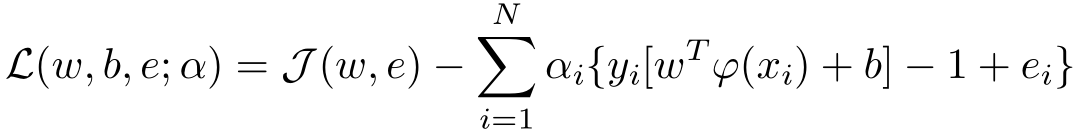
 其中α i \alpha_iαi​是拉格朗日乘子，也是支持值（support values）
  3) 求解最优化条件
  
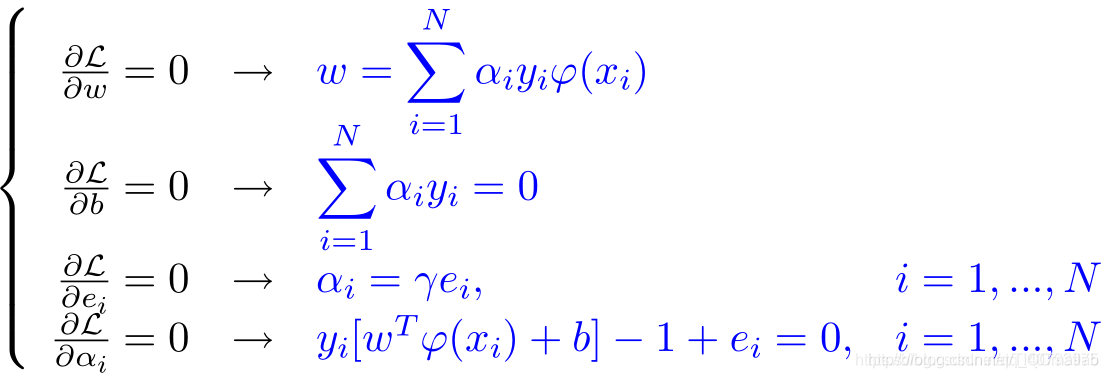
4) 求解对偶问题（与SVM同样不对w ww和e ee做任何计算）

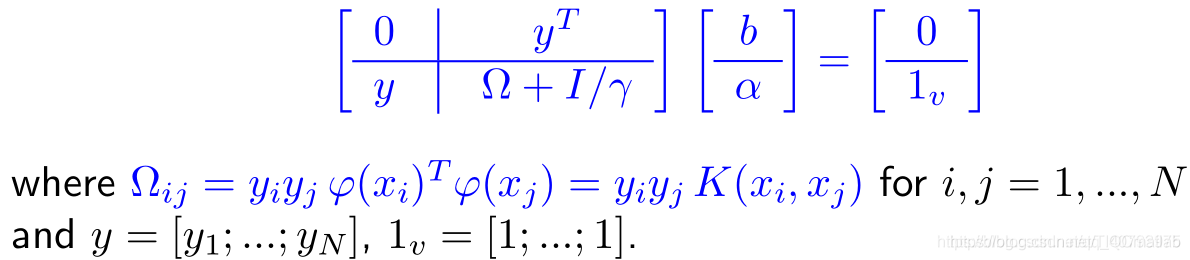
 LLSVM通过求解上述线性方程组，得到优化变量a aa和b bb的值，这种求解方式比求解QP问题更加简便

5) 与标准SVM的区别

a. 使用等式约束，而不是不等式约束；
    b. 由于对每个样本点采用了等式约束，因此对松弛向量不施加任何约束，这也是LSSVM丢失稀疏性的重要原因；
    c. 通过解决等式约束以及最小二乘问题，使得问题得到进一步简化。

LSSVM用于回归任务
  1) 问题描述
  
LSSVM的弊端
  注意到解决分类任务时，在求解最优化过程中得到α i = γ e i \alpha_{i}=\gamma{e_{i}}αi​=γei​，由于拉格朗日乘子法中对应于等式约束的拉格朗日乘子α i ≠ 0 \alpha_{i}\neq{0}αi​̸​=0，因此全部训练样本都会被作为支持向量来看待，这就会导致其丧失SVM原有的稀疏性质，但是还可以通过对训练集进行基于支持度的“减枝”（pruning）处理来达到稀疏化的目的，这一步也可以看做是一种稀疏近似（sparse approximate）操作。

二、部分源代码

%=====================================================================
%初始化
clc
close all
clear
format long
tic
%==============================================================
%%导入数据
data=xlsread('1.xlsx');
[row,col]=size(data);
x=data(:,1:col-1);
y=data(:,col);
set=1; %设置测量样本数
row1=row-set;%
train_x=x(1:row1,:);
train_y=y(1:row1,:);
test_x=x(row1+1:row,:);%预测输入
test_y=y(row1+1:row,:);%预测输出
train_x=train_x';
train_y=train_y';
test_x=test_x';
test_y=test_y';
 
%%数据归一化
[train_x,minx,maxx, train_yy,miny,maxy] =premnmx(train_x,train_y);
test_x=tramnmx(test_x,minx,maxx);
train_x=train_x';
train_yy=train_yy';
train_y=train_y';
test_x=test_x';
test_y=test_y';
%% 参数初始化
eps = 10^(-6);
%%定义lssvm相关参数
type='f';
kernel = 'RBF_kernel';
proprecess='proprecess';
lb=[0.01 0.02];%参数c、g的变化的下限
ub=[1000 100];%参数c、g的变化的上限
dim=2;%维度，即一个优化参数
SearchAgents_no=20; % Number of search agents
Max_iter=100; % Maximum numbef of iterations
n=10;      % Population size, typically 10 to 25
A=0.25;      % Loudness  (constant or decreasing)
r=0.5;      % Pulse rate (constant or decreasing)
% This frequency range determines the scalings
Qmin=0;         % Frequency minimum
Qmax=2;         % Frequency maximum
% Iteration parameters
tol=10^(-10);    % Stop tolerance
Leader_pos=zeros(1,dim);
Leader_score=inf; %change this to -inf for maximization problems
%Initialize the positions of search agents
for i=1:SearchAgents_no
    Positions(i,1)=ceil(rand(1)*(ub(1)-lb(1))+lb(1));
    Positions(i,2)=ceil(rand(1)*(ub(2)-lb(2))+lb(2));
    Fitness(i)=Fun(Positions(i,:),train_x,train_yy,type,kernel,proprecess,miny,maxy,train_y,test_x,test_y);
v(i,:)=rand(1,dim);
end
[fmin,I]=min(Fitness);
best=Positions(I,:);
Convergence_curve=zeros(1,Max_iter);
t=0;% Loop counter
% Start the iterations -- Bat Algorithm
 
 
%% 结果分析
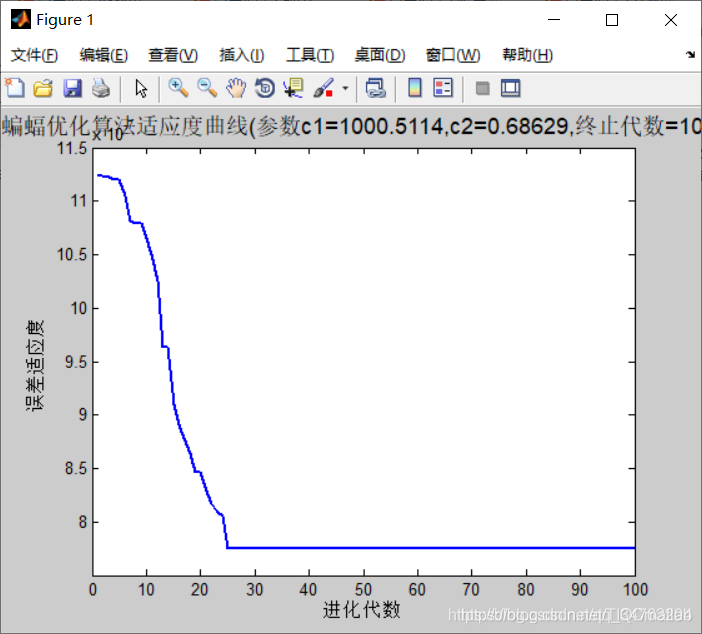
plot( Convergence_curve,'LineWidth',2);
title(['灰狼优化算法适应度曲线','(参数c1=',num2str(Leader_pos(1)),',c2=',num2str(Leader_pos(2)),',终止代数=',num2str(Max_iter),')'],'FontSize',13);
xlabel('进化代数');ylabel('误差适应度');
 
bestc = Leader_pos(1);
bestg = Leader_pos(2);
 
 
end
RD=RD'
disp(['灰狼优化算法优化svm预测误差=',num2str(D)])
 
% figure
% plot(test_predict,':og')
% hold on
% plot(test_y,'- *')
% legend('预测输出','期望输出')
% title('网络预测输出','fontsize',12)
% ylabel('函数输出','fontsize',12)
% xlabel('样本','fontsize',12)
figure
plot(train_predict,':og')
hold on
plot(train_y,'- *')
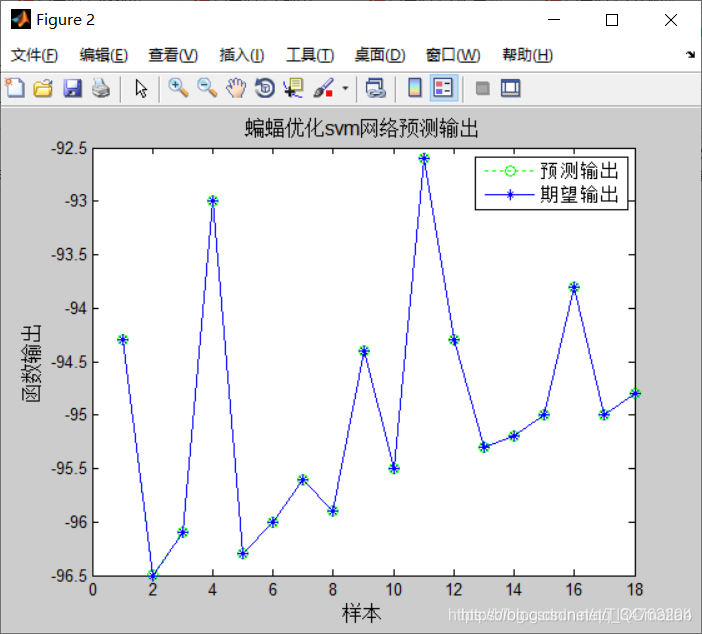
legend('预测输出','期望输出')
title('灰狼优化svm网络预测输出','fontsize',12)
ylabel('函数输出','fontsize',12)
xlabel('样本','fontsize',12)
 
toc   %计算时间
 

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/112986071