【数字信号】基于matlab 8级m序列【含Matlab源码 353期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【数字信号】基于matlab 8级m序列【含Matlab源码 353期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、8级m序列简介

1 m序列的简介
m序列是最长线性移位寄存器序列的简称。顾名思义，m序列是由多级移位寄存器或其延迟元件通过线性反馈产生的最长的码序列。在二进制移位寄存器中，若n为移位寄存器的级数，n级移位寄存器共有 2n 个状态，除去全0状态外还剩下 2n-1 中状态，因此它能产生的最大长度的码序列为 2n-1 位，也就是说，一个n级线性反馈移位寄存器产生的最长周期等于 2n-1 。在码分多址系统中主要采用两种长度的m序列：一种是周期为 215-1的m序列，又称短PN序列；另一种是周期为242-1的m序列，又称为长PN码序列。
m序列是一种基本又典型的伪随机序列。在通信领域有着广泛的应用，如扩频通信、卫星通信的码分多址（CDMA），数字数据中的加密、加扰、同步、误码率测量等领域。

2 m序列产生的原理



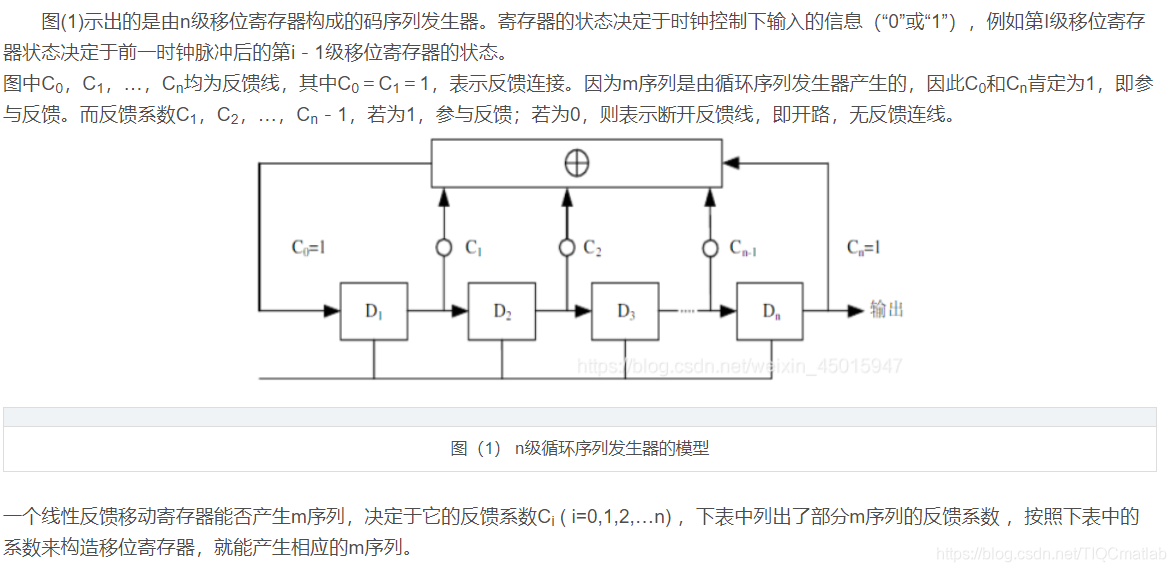
3 m序列的产生与本原多项式
由n级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器，如果反馈逻辑线路只由模2和构成，则称为线性反馈移位寄存器。带线性反馈逻辑的移位寄存器设定初始状态后，在时钟触发下，每次移位后各级寄存器会发生变化，其中任何一级寄存器的输出，随着时钟节拍的推移都会产生一个序列，该序列称为移位寄存器序列。n级线性移位寄存器如下图所示：


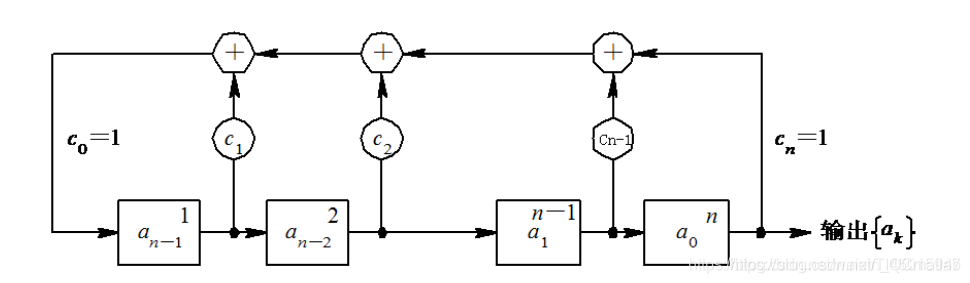
（1）F(x)是不可约的，即不能再分解多项式；
（2）F（x）可整除xn+1，这里p=2n+1；
（3）F（x）不能整除xn+1，这里q<q.
满足上述条件的多项式称为本原多项式，这样产生m序列的充要条件就变成了如何寻找本原多项式。




3 m序列的性质
m序列具有以下性质：
（1）均衡性
由m序列的一个周期中，0和1的数目基本相等。1的数目比0的数目多一个。该性质可由m序列1000010010110011111000110111010看出：总共有16个1和15个0。

（2）游程分布
m序列中取值相同的那些相继的元素合称为一个“游程”。游程中元素的个数称为游程长度。n级的m序列中，总共有2n-1个游程，其中长度为1的游程占总游程数的1/2，长度为2的游程占总游程数的1/4，长度为k的游程占总游程数的2k。且长度为k的游程中，连0与连1的游程数各占一半。如序列1000010010110011111000110111010中，游程总数为25-1=16，此序列各种长度的游程分布如下：
长度为1的游程数目为8，其中4个1游程和4个0游程；
长度为2的游程数目为4，2个11游程，2个00游程；
长度为3的游程数目为2，1个111游程，1个000游程；
长度为4的连0游程数目为1；
长度为5的连1游程数目为1。

（3）移位相加特性
一个m序列m1与其经任意延迟移位产生的另一序列m2模2相加，得到的仍是m1的某次延迟移位序列 m3，即m1与m2 异或为m3。

（4）相关特性
我们可以根据移位相加特性来验证m序列的自相关特性。因为移位相加后得到的还是m序列，因此0的个数比1的个数少1。

三、部分源代码

%---------产生8位m序列，控制频率合成器产生频率变化的高频载波---------------
clear all; 
clc; 
%---------初始化---------------
MAXCLOCK=1000000; 
PNSeq=[1 1 1 1 1 1 1 1];

InitialPNSeq=PNSeq;

k=1; %第几次选择频率
SaveFrq=[];

%---------主仿真时钟---------------
CLOCK=0; %单位是 ms/100
step=5000; %每100表示1ms
%---------产生M序列---------------

 mseq=m8();
 mseq                     %输出m序列位表示
 A=[];
 A=[mseq PNSeq];          %在m序列后添加开始状态序列，方便输出跳频序列

 subplot(211);
 plot(mseq,'-');
 xlabel('N');
 title('m序列');

%---------仿真开始---------------
while CLOCK < MAXCLOCK
CLOCK=CLOCK+step;
if mod(CLOCK,5000)==0
%---------产生M序列---------------
% 5 ms跳一次频, 每秒200跳 
%---------选择频率---------------
if (k<=255)
MixFrq=SelectFrq(A(k:k+7))/1000e3;
k=k+1;
end
SaveFrq=[SaveFrq,MixFrq];
end
% 产生n=8级m序列
function m1=m8()
n=8;
%m1序列的多项式为435（8进制）=100011101(B)
PNSeq=[1 1 1 1 1 1 1 1 ];%m1序列各移位寄存器的初态值:a1至a8
co=[];
N=2^n-1;
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社，2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社，2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/113893509