【气动学】基于matlab RBF神经网络控制卫星轨道和姿态【含Matlab源码 377期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【气动学】基于matlab RBF神经网络控制卫星轨道和姿态【含Matlab源码 377期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、RBF简介

1什么是径向基函数
1985年，Powell提出了多变量插值的径向基函数（RBF）方法。径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意一点c的距离，c点称为中心点，也就是Φ（x，c）=Φ(‖x-c‖)。任意一个满足Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数，标准的一般使用欧氏距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)2) } 其中x_c为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。

2 RBF神经网络
RBF神将网络是一种三层神经网络，其包括输入层、隐层、输出层。从输入空间到隐层空间的变换是非线性的，而从隐层空间到输出层空间变换是线性的。流图如下：

RBF网络的基本思想是：用RBF作为隐单元的“基”构成隐含层空间，这样就可以将输入矢量直接映射到隐空间，而不需要通过权连接。当RBF的中心点确定以后，这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的，即网络的输出是隐单元输出的线性加权和，此处的权即为网络可调参数。其中，隐含层的作用是把向量从低维度的p映射到高维度的h，这样低维度线性不可分的情况到高维度就可以变得线性可分了，主要就是核函数的思想。这样，网络由输入到输出的映射是非线性的，而网络输出对可调参数而言却又是线性的。网络的权就可由线性方程组直接解出，从而大大加快学习速度并避免局部极小问题。
径向基神经网络的激活函数可表示为：

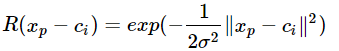
其中xp为第p个输入样本，ci为第i个中心点，h为隐含层的结点数，n是输出的样本数或分类数。径向基神经网络的结构可得到网络的输出为：

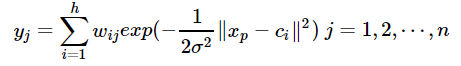
当然，采用最小二乘的损失函数表示：

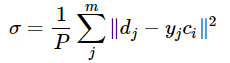
3 RBF神经网络的学习问题

求解的参数有3个：基函数的中心、方差以及隐含层到输出层的权值。
(1）自组织选取中心学习方法：
第一步：无监督学习过程，求解隐含层基函数的中心与方差
第二步：有监督学习过程，求解隐含层到输出层之间的权值
首先，选取h个中心做k-means聚类，对于高斯核函数的径向基，方差由公式求解：
cmax为所选取中心点之间的最大距离。
隐含层至输出层之间的神经元的连接权值可以用最小二乘法直接计算得到，即对损失函数求解关于w的偏导数，使其等于0，可以化简得到计算公式为：
（2）直接计算法
隐含层神经元的中心是随机地在输入样本中选取，且中心固定。一旦中心固定下来，隐含层神经元的输出便是已知的，这样的神经网络的连接权就可以通过求解线性方程组来确定。适用于样本数据的分布具有明显代表性。
（3）有监督学习算法
通过训练样本集来获得满足监督要求的网络中心和其他权重参数，经历一个误差修正学习的过程，与BP网络的学习原理一样，同样采用梯度下降法。因此RBF同样可以被当作BP神经网络的一种。

4 RBF神经网络与BP神经网络之间的区别
4.1 局部逼近与全局逼近
BP神经网络的隐节点采用输入模式与权向量的内积作为激活函数的自变量，而激活函数采用Sigmoid函数。各调参数对BP网络的输出具有同等地位的影响，因此BP神经网络是对非线性映射的全局逼近。
RBF神经网络的隐节点采用输入模式与中心向量的距离（如欧式距离）作为函数的自变量，并使用径向基函数（如Gaussian函数）作为激活函数。神经元的输入离径向基函数中心越远，神经元的激活程度就越低（高斯函数）。RBF网络的输出与部分调参数有关，譬如，一个wij值只影响一个yi的输出，RBF神经网络因此具有“局部映射”特性。

所谓局部逼近是指目标函数的逼近仅仅根据查询点附近的数据。而事实上，对于径向基网络，通常使用的是高斯径向基函数，函数图象是两边衰减且径向对称的，当选取的中心与查询点（即输入数据）很接近的时候才对输入有真正的映射作用，若中心与查询点很远的时候，欧式距离太大的情况下，输出的结果趋于0，所以真正起作用的点还是与查询点很近的点，所以是局部逼近；而BP网络对目标函数的逼近跟所有数据都相关，而不仅仅来自查询点附近的数据。

4.2 中间层数的区别
BP神经网络可以有多个隐含层，但是RBF只有一个隐含层。

4.3 训练速度的区别
使用RBF的训练速度快，一方面是因为隐含层较少，另一方面，局部逼近可以简化计算量。对于一个输入x，只有部分神经元会有响应，其他的都近似为0，对应的w就不用调参了。

4.4 RBF网络是连续函数的最佳逼近，而BP网络不是。

三、部分源代码

clc;clear all;close all;
mu = 3.986004418e14;
al = 7400000; %参考星轨道半长轴(m)
n = sqrt(mu/(al^3));%参考星平均角速度
N = 2;
T = 2*pi/n;
t0 = 0;
tf = t0 + N*T;

x0=[0.3;-0.1;0.2;-0.2;0.12;0.17;-0.09];
% xt0=[0.3;-0.1;0.2;-0.2;0.12;0.17;-0.09;-1.3;-3.05;1.22];
% [t,x]=ode45('zitai_function',[t0:17:tf],x0);
% [t,xt]=ode45('zitai_ctrl',[t0:17:tf],xt0); 
% [t,xq]=ode45('oula',[t0:17:tf],[-1.3;-3.05;1.22]);
[t,x]=ode45('rbf_zitai',[t0:17:5000],x0);

% c0=pi/T;
% wrd=[-c0*sin(2*c0*t) 1.6*c0*sin(4*c0*t) 0.8*c0*sin(2*c0*t)];
% wr=[xt(:,5)-wrd(1,1) xt(:,6)-wrd(2,1) xt(:,7)-wrd(3,1)];
% fai=xq(:,1);sita=xq(:,2);pesi=xq(:,3);
% for i=1:1118
% q(i,1)=cos(pesi(i,:)/2)*sin(fai(i,:)/2)*cos(sita(i,:)/2)-sin(pesi(i,:)/2)*cos(fai(i,:)/2)*sin(sita(i,:)/2);
% q(i,2)=cos(pesi(i,:)/2)*cos(fai(i,:)/2)*sin(sita(i,:)/2)+sin(pesi(i,:)/2)*sin(fai(i,:)/2)*cos(sita(i,:)/2);
% q(i,3)=sin(pesi(i,:)/2)*cos(fai(i,:)/2)*cos(sita(i,:)/2)+cos(pesi(i,:)/2)*sin(fai(i,:)/2)*sin(sita(i,:)/2);
% q(i,4)=cos(pesi(i,:)/2)*cos(fai(i,:)/2)*cos(sita(i,:)/2)-sin(pesi(i,:)/2)*sin(fai(i,:)/2)*sin(sita(i,:)/2);
% end
unction dx=rbf_micishedong(t,x)
mu=398600.44e+9;
rol=7400000;
Re = 6378000;%地球赤道半径
el = 0; %偏心率
il = 30*pi/180;   %轨道倾角
Ml = 90*pi/180; %平近点角
nl = sqrt(mu/rol^3);
wl = 0*pi/180; %近地点辐角
raanl = 100*pi/180;  %升交点赤经
fl = 160.0513*pi/180;%真近点角
ul = wl+fl;%真纬度角
J2 = 1.08263e-3;
A=[cos(ul)*cos(raanl)-sin(ul)*cos(il)*sin(raanl) cos(ul)*sin(raanl)+sin(ul)*cos(il)*cos(raanl) sin(ul)*sin(il);
   -sin(ul)*cos(raanl)-cos(ul)*cos(il)*sin(raanl) -sin(ul)*sin(raanl)+cos(ul)*cos(il)*cos(raanl) cos(ul)*sin(il);
   sin(il)*sin(raanl) -sin(il)*cos(raanl) cos(il)];%地心惯性坐标系到参考航天器的坐标转换矩阵
fal1=sqrt(mu*rol*(1-el^2))*(1+2*el*cos(Ml)+el^2*0.5*(1+5*cos(2*Ml)+el^3))/rol^2;
fal2=2*sqrt(mu*rol*(1-el^2))*(el*nl*sin(Ml)+el^2*(nl*sin(2*Ml)+3*nl*cos(Ml)*sin(Ml))+el^3)/rol^2;
c=diag([0.1;0.1;0.1]);
% tao=diag([0.05;0.05;0.05]);
beta=0.05;
b=133*eye(3);
% f0=[1;1;1];
% D0=diag([0.5;0.5;0.5]);

xp=[x(7);x(8);x(9)];
xp1=[x(10);x(11);x(12)];
xpd=[x(1);x(2);x(3)];
xpd1=[x(4);x(5);x(6)];
e=xp-xpd;
e1=xp1-xpd1;
s=e1+c*e;
xpd2=[nl^2*x(1)+0*x(2)+2*nl*x(5)+2*nl^2*x(1);
      -0*x(1)+nl^2*x(2)-2*nl*x(4)-nl^2*x(2);
      -nl^2*x(3);];
% xpd2=[0.1;-0.6;-0.5];
XYZ=inv(A)*[rol+x(7);x(8);x(9)];
X=XYZ(1,1);Y=XYZ(2,1);Z=XYZ(3,1);
R=sqrt(X^2+Y^2+Z^2);%考虑地球J2摄动时随时间变化的位置半径
gx1=-mu*x(7)/R^3*(1+1.5*J2*((Re/R)^2)*(1-5*(x(9)^2)/R^2));%地球J2摄动下X方向的地球引力项
gy1=-mu*x(8)/R^3*(1+1.5*J2*((Re/R)^2)*(1-5*(x(9)^2)/R^2));%地球J2摄动下Y方向的地球引力项
gz1=-mu*x(9)/R^3*(1+1.5*J2*((Re/R)^2)*(3-5*(x(9)^2)/R^2));%地球J2摄动下Z方向的地球引力项
gxyz=A*[gx1;gy1;gz1];
gx=gxyz(1,1);gy=gxyz(2,1);gz=gxyz(3,1);

x0=[zeros(1,3),120];
c1=[-0.5 0 0.5;
   -0.5 0 0.5];
b=2;
node=3;
yd=[x(7) x(8) x(9)];
dyd=[x(10) x(11) x(12)];
ddyd=[2*nl*x(11)+3*nl^2*x(7) -2*nl*x(10) -nl^2*x(9)];

e=[x(7)-x(1) x(8)-x(2) x(9)-x(3)];
de=[x(10)-x(4) x(11)-x(5) x(12)-x(6)];

kp=0.5;
kd=0.3;
K=[kp kd]';
E=[e;de];
Fai=[0 1;-kp -kd];
A=Fai';
Q=[500 0;0 500];
P=lyap(A,Q);

W=[x(10) x(11) x(12)]';
xi=[e;de];
h=zeros(3,1);
for j=1:1:3
    h(j)=exp(-norm(xi(:,j)-c1(:,j))^2/(2*b^2));
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
 

四、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 门云阁.MATLAB物理计算与可视化[M].清华大学出版社，2013.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/113995676