【用电量预测】基于matlab SVM用电量预测【含Matlab源码 103期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【用电量预测】基于matlab SVM用电量预测【含Matlab源码 103期】

二、SVM简介

机器学习的一般框架：
训练集 => 提取特征向量 => 结合一定的算法（分类器：比如决策树、KNN）=>得到结果
1 SVM定义
支持向量机（support vector machines，SVM）是一种二分类模型，它将实例的特征向量映射为空间中的一些点，SVM 的目的就是想要画出一条线，以 “最好地” 区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。SVM 适合中小型数据样本、非线性、高维的分类问题。

SVM 最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出，目前的版本（soft margin）是由 Corinna Cortes 和 Vapnik 在1993年提出，并在1995年发表。深度学习（2012）出现之前，SVM 被认为机器学习中近十几年来最成功，表现最好的算法。

2 SVM 基本概念
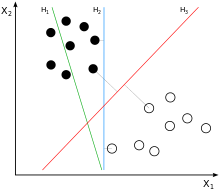
将实例的特征向量（以二维为例）映射为空间中的一些点，如下图的实心点和空心点，它们属于不同的两类。SVM 的目的就是想要画出一条线，以“最好地”区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。

Q1：能够画出多少条线对样本点进行区分？
答：线是有无数条可以画的，区别就在于效果好不好，每条线都可以叫做一个划分超平面。比如上面的绿线就不好，蓝线还凑合，红线看起来就比较好。我们所希望找到的这条效果最好的线就是具有 “最大间隔的划分超平面”。

Q2：为什么要叫作“超平面”呢？
答：因为样本的特征很可能是高维的，此时样本空间的划分就不是一条线了。

Q3：画线的标准是什么？/ 什么才叫这条线的效果好？/ 哪里好？
答：SVM 将会寻找可以区分两个类别并且能使间隔（margin）最大的划分超平面。比较好的划分超平面，样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。

Q4：间隔（margin）是什么？
答：对于任意一个超平面，其两侧数据点都距离它有一个最小距离（垂直距离），这两个最小距离的和就是间隔。比如下图中两条虚线构成的带状区域就是 margin，虚线是由距离中央实线最近的两个点所确定出来的（也就是由支持向量决定）。但此时 margin 比较小，如果用第二种方式画，margin 明显变大也更接近我们的目标。


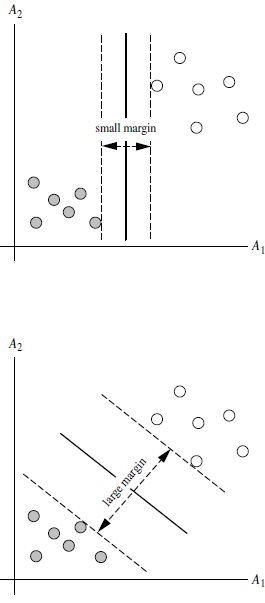
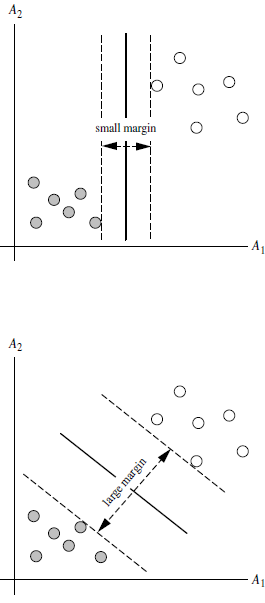
Q5：为什么要让 margin 尽量大？
答：因为大 margin 犯错的几率比较小，也就是更鲁棒啦。

Q6：支持向量是什么？
答：从上图可以看出，虚线上的点到划分超平面的距离都是一样的，实际上只有这几个点共同确定了超平面的位置，因此被称作 “支持向量（support vectors）”，“支持向量机” 也是由此来的。

三、部分源代码

clear all;
clc ;
close all
%得到文件路径，找到所有.dat格式的文件
sh = xlsread('data.xlsx','Sheet1','B2:B38');
addpath('./libsvm-3.20');%%添加工具箱
%extract data
[m,n] = size(sh);
n1 = round(length(sh)*0.7);%训练样本大小
ts = sh(1:n1,1);%训练数据
tsx = sh(n1+1:m,1);%测试数据
original = sh(n1+1:end,:);%原始测试数据
%归一化处理
[TS,TSps] = mapminmax(ts);
[TSX,TSXps] = mapminmax(tsx);
[TSX_zong,TSXps_zong] = mapminmax(sh);
%split the data into training and testing

train_label = TS(1:n1,:);%训练数据标签
train_data = TS(1:n1,:);%训练数据
test_label = TSX(1:end,:);%测试数据标签
test_data = TSX(1:end,:);%测试数据
test_label_zong = TSX_zong(1:end,:);%测试数据标签
test_data_zong = TSX_zong(1:end,:);%测试数据
% Find the optimize value of c,g paramter
% Approximately choose the parameters:
% the scale of c is 2^(-5),2^(-4),...,2^(10)
% the scale of g is 2^(-5),2^(-4),...,2^(5)
[bestmse,bestc,bestg] = svmregress(train_label,train_label,-5,10,-5,5,3,1,1,0.0005);

% Display the approximate result
disp('Display the approximate result');
str = sprintf( 'Best Cross Validation MSE = %g Best c = %g Best g = %g',bestmse,bestc,bestg);
disp(str);
%Do training by using svmtrain of libsvm
cmd = ['-c ', num2str(bestc), ' -g ', num2str(bestg) , ' -s 3 -p 0.01'];
model = svmtrain(train_label,train_data,cmd);%训练
%Do predicting by using svmpredict of libsvm
 clear all;
clc ;
close all
%得到文件路径，找到所有.dat格式的文件
sh = xlsread('data.xlsx','Sheet1','B2:B38');
addpath('./libsvm-3.20');%%添加工具箱
%extract data
[m,n] = size(sh);
n1 = round(length(sh)*0.7);%训练样本大小
ts = sh(1:n1,1);%训练数据
tsx = sh(n1+1:m,1);%测试数据
original = sh(n1+1:end,:);%原始测试数据
%归一化处理
[TS,TSps] = mapminmax(ts);
[TSX,TSXps] = mapminmax(tsx);
[TSX_zong,TSXps_zong] = mapminmax(sh);
%split the data into training and testing

train_label = TS(1:n1,:);%训练数据标签
train_data = TS(1:n1,:);%训练数据
test_label = TSX(1:end,:);%测试数据标签
test_data = TSX(1:end,:);%测试数据
test_label_zong = TSX_zong(1:end,:);%测试数据标签
test_data_zong = TSX_zong(1:end,:);%测试数据
% Find the optimize value of c,g paramter
% Approximately choose the parameters:
% the scale of c is 2^(-5),2^(-4),...,2^(10)
% the scale of g is 2^(-5),2^(-4),...,2^(5)
[bestmse,bestc,bestg] = svmregress(train_label,train_label,-5,10,-5,5,3,1,1,0.0005);

% Display the approximate result
disp('Display the approximate result');
str = sprintf( 'Best Cross Validation MSE = %g Best c = %g Best g = %g',bestmse,bestc,bestg);
disp(str);
%Do training by using svmtrain of libsvm
cmd = ['-c ', num2str(bestc), ' -g ', num2str(bestg) , ' -s 3 -p 0.01'];
model = svmtrain(train_label,train_data,cmd);%训练
%Do predicting by using svmpredict of libsvm

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/112504598