【数学建模】基于matlab时变参数随机波动率向量自回归模型（TVP-VAR）【含Matlab源码 037期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【数学建模】基于matlab时变参数随机波动率向量自回归模型（TVP-VAR）【含Matlab源码 037期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、部分源代码

%==================================4.1 Main================================
clear;
clc;
 
% Load Korobilis (2008) quarterly data
load ydata.dat; % data 
load yearlab.dat; % data labels 
 
%%
%----------------------------------BASICS----------------------------------
 
 
Y=ydata;
t=size(Y,1);        % t - The total number of periods in the raw data (t=215)
M=size(Y,2);        % M - The dimensionality of Y (i.e. the number of variables)(M=3)
tau = 40;           % tau - the size of the training sample (the first forty quarters)
p = 2;              % p - number of lags in the VAR model 
 
%% Generate the Z_t matrix, i.e. the regressors in the model. 
 
ylag = mlag2(Y,p);          % This function generates a 215x6 matrix with p lags of variable Y. 
ylag = ylag(p+tau+1:t,:);   % Then remove our training sample, so now a 173x6 matrix. 
 
K = M + p*(M^2);            % K is the number of elements in the state vector
 
% Here we distribute the lagged y data into the Z matrix so it is
% conformable with a beta_t matrix of coefficients. 
 
Z = zeros((t-tau-p)*M,K);   
for i = 1:t-tau-p
    ztemp = eye(M);
    for j = 1:p        
        xtemp = ylag(i,(j-1)*M+1:j*M); 
        xtemp = kron(eye(M),xtemp);
        ztemp = [ztemp xtemp];
    end
    Z((i-1)*M+1:i*M,:) = ztemp;
end
 
% Redefine our variables to exclude the training sample and the first two
% lags that we take as given, taking total number of periods (t) from 215 
% to 173. 
 
y = Y(tau+p+1:t,:)';
yearlab = yearlab(tau+p+1:t);
t=size(y,2); % t now equals 173
 
%% --------------------MODEL AND GIBBS PRELIMINARIES-----------------------
 
nrep = 5000;    % Number of sample draws 
nburn = 2000;   % Number of burn-in-draws
it_print = 100; % Print in the screen every "it_print"-th iteration
 
 
%% INITIAL STATE VECTOR PRIOR  
 
% We use the first 40 observations (tau) to run a standard OLS of the
% measurement equation, using the function ts_prior. The result is
% estimates for priors for B_0 and Var(B_0). 
 
[B_OLS,VB_OLS]= ts_prior(Y,tau,M,p);
 
% Given the distributions we have, we now have to define our priors for B,
% Q and Sigma. These are set in accordance with how they are set in 
% Primiceri (2005). These are the hyperparameters of the beta, Q and Sigma
% initial priors. 
 
B_0_prmean = B_OLS;
B_0_prvar = 4*VB_OLS; 
 
Q_prmean = ((0.01).^2)*tau*VB_OLS;
Q_prvar = tau;
 
Sigma_prmean = eye(M);
Sigma_prvar = M+1;
 
% To start the Kalman filtering assign arbitrary values that are in support
% of their priors, Q and Sigma. 
 
consQ = 0.0001;
Qdraw = consQ*eye(K);
Sigmadraw = 0.1*eye(M);
 
% Create some matrices for storage that will be filled in once we
% start the Gibbs sampling.
 
Btdraw = zeros(K,t); 
Bt_postmean = zeros(K,t);
Qmean = zeros(K,K);
Sigmamean = zeros(M,M);
 
%% -------------------------IRF-PRELIMINARIES------------------------------
nhor = 21;     % The number of periods in the impulse response function. 
 
% Matricies to be filled containing IRFs for 1975q1, 1981q3, 1996q1. The 
% dimensions correspond to the iterations of the gibbs sample, each of the
% variables, and each of the 21 periods of the IRF analysis. 
 
imp75 = zeros(nrep,M,nhor); 
imp81 = zeros(nrep,M,nhor);
imp96 = zeros(nrep,M,nhor);
 
% This corresponds to variable J introduced in equation (14) in the report
 
bigj = zeros(M,M*p); 
bigj(1:M,1:M) = eye(M);
 
 
%% ================ START GIBBS SAMPLING ==================================
 
tic; % This is just a timer
disp('Number of iterations');
 
 
for irep = 1:nrep + nburn    % 7000 gibbs iterations starts here
    % Print iterations - this just updates on the progress of the sampling
    if mod(irep,it_print) == 0
        disp(irep);toc;
    end
    
%% Draw 1: B_t from p(B_t|y,Sigma)
    
    % We use the function 'carter_kohn_hom' to to run the FFBS algorithm. 
    % This results in a 21x173 matrix, corresponding to one Gibbs sample
    % draw of each of the coefficients in each time period. The inputs
    % Sigmadraw and Qdraw are updated for each Gibbs sample repetition.
    
    [Btdraw] = carter_kohn_hom(y,Z,Sigmadraw,Qdraw,K,M,t,B_0_prmean,B_0_prvar);
    
  
%% Draw 2: Q from p(Q^{-1}|y,B_t) which is i-Wishart
 
    % We draw Q from an Inverse Wishart distribution. The parameters 
    % of the distribution are derived as equation (11) in the main report.
    % The mean is taken as the inverse of the accumulated sum of squared 
    % errors added to the prior mean, and the variance is simply t.  
    
    % Differencing Btdraw to create the sum of squared errors
    
    Btemp = Btdraw(:,2:t)' - Btdraw(:,1:t-1)'; 
    sse_2Q = zeros(K,K);
    for i = 1:t-1
        sse_2Q = sse_2Q + Btemp(i,:)'*Btemp(i,:);
    end
 
    Qinv = inv(sse_2Q + Q_prmean);      % compute mean to use for Wishart draw
    Qinvdraw = wish(Qinv,t+Q_prvar);    % draw inv q from the wishart distribution
    Qdraw = inv(Qinvdraw);              % find non-inverse q 
    
%% Draw 3: Sigma from p(Sigma|y,B_t) which is i-Wishart
 
    % We draw Sigma from an Inverse Wishart distribution. The parameters 
    % of the distirbution are derived as equation (10) in the main report. 
    % The mean is taken as the inverse of the sum of squared residuals
    % added to the prior mean. The variance is simply t. 
    
    % Find residuals using data and the current draw of coefficients
    
    resids = zeros(M,t);
    for i = 1:t
        resids(:,i) = y(:,i) - Z((i-1)*M+1:i*M,:)*Btdraw(:,i);
    end
    
    % Create a matrix for the accumulated sum of squared residuals, to
    % be used as the mean parameter in the i-Wishart draw below. 
    sse_2S = zeros(M,M);
    for i = 1:t
        sse_2S = sse_2S + resids(:,i)*resids(:,i)';
    end
    
    Sigmainv = inv(sse_2S + Sigma_prmean);          % compute mean to use for the Wishart
    Sigmainvdraw = wish(Sigmainv,t+Sigma_prvar);    % draw from the Wishsart distribution
    Sigmadraw = inv(Sigmainvdraw);                  % turn into non-inverse Sigma
    
%% IRF 
    % We only apply IRF analysis once we have exceeded the burn-in draws phase.
    if irep > nburn;         
            
            % Create matrix that is going to contain all beta draws over
            % which we will take the mean after the Gibbs sampler as our moment
            % estimate: 
            Bt_postmean = Bt_postmean + Btdraw;
            
            % biga is the A matrix of the VAR(1) version of our VAR(2) model, 
            % found in equation (12. biga changes in every period of the 
            % analysis, because the coefficients are time varying, so we 
            % apply the analysis below in every time period. 
            
            biga = zeros(M*p,M*p); 
            for j = 1:p-1
                biga(j*M+1:M*(j+1),M*(j-1)+1:j*M) = eye(M); % fill the A matrix with identity matrix (3) in bottom left corner
            end
 
            % The following procedure is applied separately in each time period. 
            
            % This loop takes coefficients of the relevant time period from
            % Bt_draw (which contains all coefficients for all t) and uses
            % them to update the biga matrix, so that it can change for
            % every t. 
            
            for i = 1:t 
                bbtemp = Btdraw(M+1:K,i);  % get the draw of B(t) at time i=1,...,T  (exclude intercept)
                splace = 0;
                for ii = 1:p
                    for iii = 1:M
                        biga(iii,(ii-1)*M+1:ii*M) = bbtemp(splace+1:splace+M,1)'; % Load non-intercept coefficient draws
                        splace = splace + M;
                    end
                end
                
                % Next we want to create a shock matrix in which the third
                % column is [0 0 1]', therefore implementing a unit shock
                % in the interest rate. 
                
                shock = eye(3);
                
                % Now get impulse responses for 1 through nhor future
                % periods. impresp is a 3x63 matrix which contains 9
                % response values in total for each period, 3 for each 
                % variable. These three responses correspond to the 3
                % possible shocks that are contained in the schock
                % matrix
                
                % bigai is updated through mulitiplication with the 
                % coefficient matrix after each time period. 
                                
                % Create a results matrix to store impulse responses in all periods
                impresp = zeros(M,M*nhor); 
                
                % Fill in the first period of the results matrix with the shock (as defined above) 
                impresp(1:M,1:M) = shock;
                
                % Create a separate variable for the a matrix so that we
                % can update it for each period of the IRF analysis. 
                bigai = biga; 
                
                % This follows the impulse response function as in equation 15.
                % Fill in each period of the results matrix according to
                % the impulse response function formula. 
                
                for j = 1:nhor-1
                    impresp(:,j*M+1:(j+1)*M) = bigj*bigai*bigj'*shock;
                    bigai = bigai*biga; % update the coefficient matrix for next period
                end
 
                % The section below keeps only the responses that we are interested in:
                % - those from the periods 1975q1, 1981q3, and 1996q1
                % - those that correspond to the shock in the interest 
                % rate (i.e. those caused by the third column of our shock
                % matrix). 
                
                if yearlab(i,1) == 1975.00;   % store only IRF from 1975:Q1
                    impf_m = zeros(M,nhor);
                    jj=0;
                    for ij = 1:nhor
                        jj = jj + M;    % select only the third column for each time period of the IRF
                        impf_m(:,ij) = impresp(:,jj);
                    end           
                % For each iteration of the Gibbs sampler, fill in the
                % results along the first dimension 
                    imp75(irep-nburn,:,:) = impf_m; 
                end
                
                if yearlab(i,1) == 1981.50;   % store only IRF from 1981:Q3
                    impf_m = zeros(M,nhor);
                    jj=0;
                    for ij = 1:nhor
                        jj = jj + M;    % select only the third column for each time period of the IRF
                        impf_m(:,ij) = impresp(:,jj);
                    end
                % For each iteration of the Gibbs sample, fill in the
                % results along the first dimension 
                    imp81(irep-nburn,:,:) = impf_m; 
                end
                
                if yearlab(i,1) == 1996.00;   % store only IRF from 1996:Q1
                    impf_m = zeros(M,nhor);
                    jj=0;
                    for ij = 1:nhor
                        jj = jj + M;    % select only the third column for each time period of the IRF
                        impf_m(:,ij) = impresp(:,jj);
                    end
                % For each iteration of the Gibbs sample, fill in the
                % results along the first dimension 
                    imp96(irep-nburn,:,:) = impf_m; 
                end
            end % End getting impulses for each time period 
        end % End the impulse response calculation section   
end % End main Gibbs loop (for irep = 1:nrep+nburn)
 
clc;
toc; % Stop timer and print total time
%% ================ END GIBBS SAMPLING ==================================
 
% Even though it is not used in our IRF analysis since we are integrating
% that into the Gibbs sampling loop, here is how to take the mean of the 
% draw of the betas as moment estimate:
 
Bt_postmean = Bt_postmean./nrep;
 
%% Graphs and tables
 
% This works out the percentage range of that each variable's coefficient
% spans across time. I.e. to what extent was the TVP facility used by each
% variable in the model? This is calculated by finding the range for each
% variable as a percentage of the mean coefficient size for that variable.
% The result is a 21x1 vector, and it is reshaped into a 3x7 matrix in order
% to map onto the system of equations (2,3,and 4) set out in the report.
 
Bt_range = ones(21,1)
for i = 1:21
    Bt_range(i) = abs((max(Bt_postmean(i,:))-min(Bt_postmean(i,:)))/mean(Bt_postmean(i,:)))
end 
Bt_range = reshape(Bt_range,3,7)
 
% Create a table of coefficient ranges for export to the report
 
rowNames = {'Inflation','Unemployment','Interest Rate'};
colNames = {'Intercept','Inf_1','Unemp_1', 'IR_1','Inf_2','Unemp_2', 'IR_2'};
pc_change_table = array2table(Bt_range,'RowNames',rowNames,'VariableNames',colNames)
 
writetable(pc_change_table,'pc_change.csv')
 
% Now plot a separate chart for each of the coefficients
 
figure
for i = 1:21       
    subplot(7,3,i)
    plot(1:t,Bt_postmean(i,:))  
end 
 
% Now we move to plotting the IRF. This section takes moments along the
% first dimension, i.e. across the Gibbs sample iterations. The moments
% are for the 16th, 50th and 84th percentile. 
 
    qus = [.16, .5, .84];
    imp75XY=squeeze(quantile(imp75,qus)); 
    imp81XY=squeeze(quantile(imp81,qus));
    imp96XY=squeeze(quantile(imp96,qus));
    
    % Plot impulse responses
    figure       
    set(0,'DefaultAxesColorOrder',[0 0 0],...
        'DefaultAxesLineStyleOrder','--|-|--')
    subplot(3,3,1)
    plot(1:nhor,squeeze(imp75XY(:,1,:)))
    title('Impulse response of inflation, 1975:Q1')
    xlim([1 nhor])
    ylim([-0.2 0.1])
%    % yline(0)
    set(gca,'XTick',0:3:nhor)
    subplot(3,3,2)
    plot(1:nhor,squeeze(imp75XY(:,2,:)))
    title('Impulse response of unemployment, 1975:Q1')
    xlim([1 nhor])
    ylim([-0.2 0.2])
   % yline(0)
    set(gca,'XTick',0:3:nhor)    
    subplot(3,3,3)
    %ylim([0 1])
%    % yline(0)
    plot(1:nhor,squeeze(imp75XY(:,3,:)))
    title('Impulse response of interest rate, 1975:Q1')
    xlim([1 nhor])
    %ylim([-0.3 0.1])
   % yline(0)
    set(gca,'XTick',0:3:nhor)    
    subplot(3,3,4)
    plot(1:nhor,squeeze(imp81XY(:,1,:)))
    title('Impulse response of inflation, 1981:Q3')
    xlim([1 nhor])
    ylim([-0.2 0.1])
   % yline(0)
    set(gca,'XTick',0:3:nhor)    
    subplot(3,3,5)
    plot(1:nhor,squeeze(imp81XY(:,2,:)))
    title('Impulse response of unemployment, 1981:Q3')
    xlim([1 nhor])
    ylim([-0.2 0.2])
   % yline(0)
    set(gca,'XTick',0:3:nhor)    
    subplot(3,3,6)
    plot(1:nhor,squeeze(imp81XY(:,3,:)))
    title('Impulse response of interest rate, 1981:Q3')
    xlim([1 nhor])
    %ylim([-0.4 0.1])
   % yline(0)
    set(gca,'XTick',0:3:nhor)    
    subplot(3,3,7)
    plot(1:nhor,squeeze(imp96XY(:,1,:)))
    title('Impulse response of inflation, 1996:Q1')
    xlim([1 nhor])
    ylim([-0.2 0.1])
   % yline(0)
    set(gca,'XTick',0:3:nhor)    
    subplot(3,3,8)
    plot(1:nhor,squeeze(imp96XY(:,2,:)))
    title('Impulse response of unemployment, 1996:Q1')
    xlim([1 nhor])
    ylim([-0.2 0.2])
   % yline(0)
    set(gca,'XTick',0:3:nhor)
    subplot(3,3,9)
    plot(1:nhor,squeeze(imp96XY(:,3,:)))
    title('Impulse response of interest rate, 1996:Q1')
    xlim([1 nhor])
     %ylim([0 1])
    % yline(0)
    set(gca,'XTick',0:3:nhor)
    
disp('             ')
disp('To plot impulse responses, use:         plot(1:nhor,squeeze(imp75XY(:,VAR,:)))           ')
disp('             ')
disp('where VAR=1 for impulses of inflation, VAR=2 for unemployment and VAR=3 for interest rate')

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
  
209
  
210
  
211
  
212
  
213
  
214
  
215
  
216
  
217
  
218
  
219
  
220
  
221
  
222
  
223
  
224
  
225
  
226
  
227
  
228
  
229
  
230
  
231
  
232
  
233
  
234
  
235
  
236
  
237
  
238
  
239
  
240
  
241
  
242
  
243
  
244
  
245
  
246
  
247
  
248
  
249
  
250
  
251
  
252
  
253
  
254
  
255
  
256
  
257
  
258
  
259
  
260
  
261
  
262
  
263
  
264
  
265
  
266
  
267
  
268
  
269
  
270
  
271
  
272
  
273
  
274
  
275
  
276
  
277
  
278
  
279
  
280
  
281
  
282
  
283
  
284
  
285
  
286
  
287
  
288
  
289
  
290
  
291
  
292
  
293
  
294
  
295
  
296
  
297
  
298
  
299
  
300
  
301
  
302
  
303
  
304
  
305
  
306
  
307
  
308
  
309
  
310
  
311
  
312
  
313
  
314
  
315
  
316
  
317
  
318
  
319
  
320
  
321
  
322
  
323
  
324
  
325
  
326
  
327
  
328
  
329
  
330
  
331
  
332
  
333
  
334
  
335
  
336
  
337
  
338
  
339
  
340
  
341
  
342
  
343
  
344
  
345
  
346
  
347
  
348
  
349
  
350
  
351
  
352
  
353
  
354
  
355
  
356
  
357
  
358
  
359
  
360
  
361
  
362
  
363
  
364
  
365
  
366
  
367
  
368
  
369
  
370
  
371
  
372
  
373
  
374
  
375
  
376
  
377
  
378
  
379
  
380
  
381
  
382
  
383
  
384
  
385
  
386
  
387
  
388
  
389
  
390
  
391
  
392
  
393
  
394
  
395
  
396
  
397
  
398
  
399
  
400
  
401
  
402
  
403
  
404
  
405
  
406
  
407
  
408
  
409
  
410
  
411
  
412
  
413
  
414
 

三、运行结果

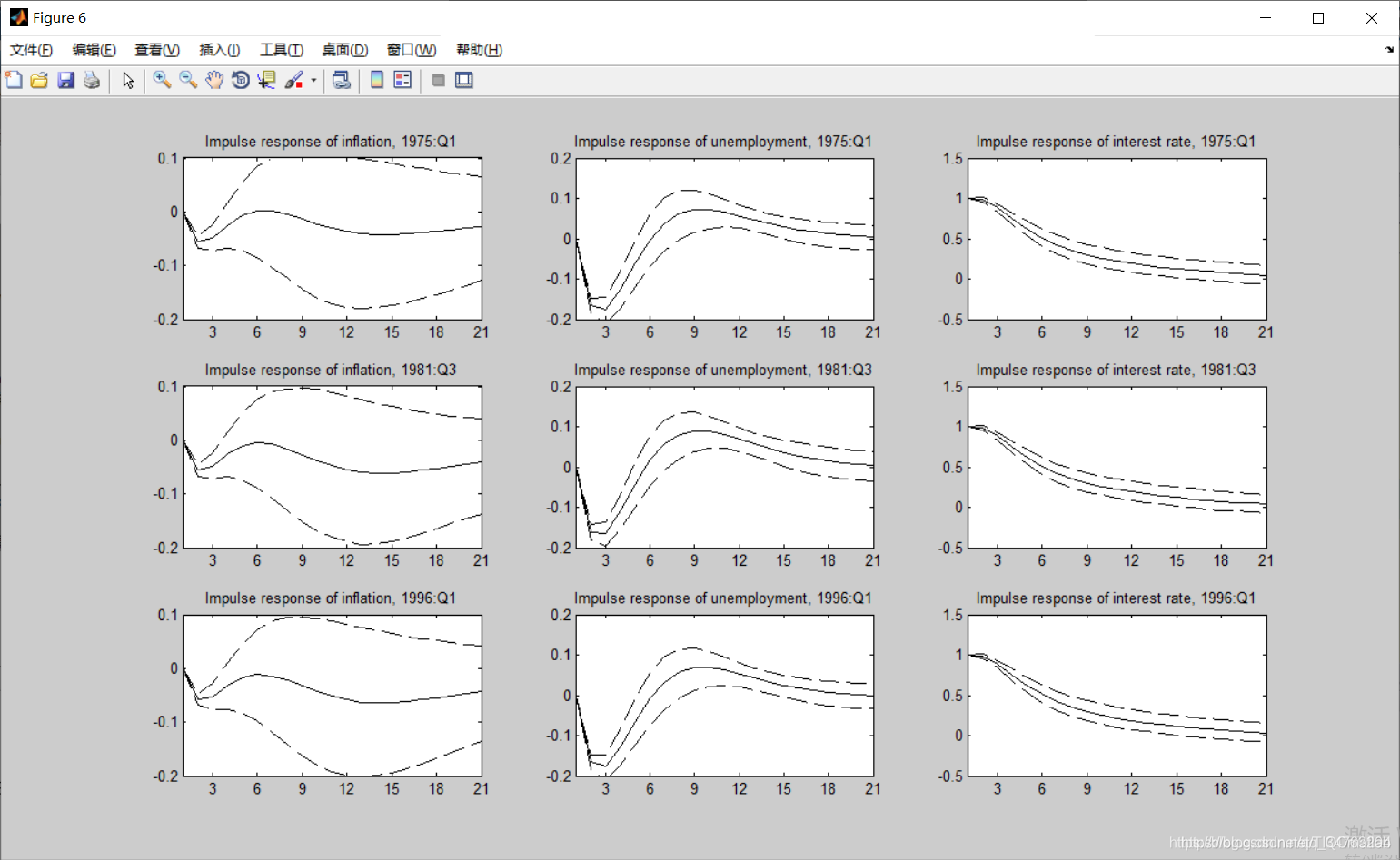
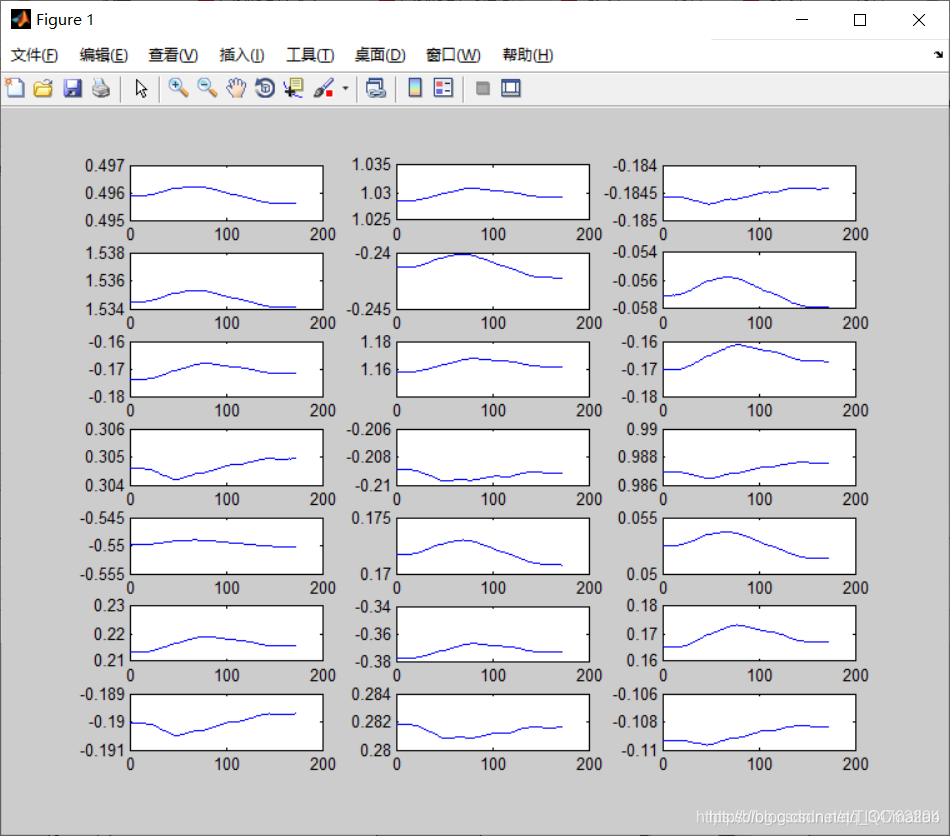
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]李昕.MATLAB数学建模[M].清华大学出版社.2017
[2]王健,赵国生.MATLAB数学建模与仿真[M].清华大学出版社.2016
[3]余胜威.MATLAB数学建模经典案例实战[M].清华大学出版社.2015

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/112152864