【APF三维路径规划】基于matlab人工势场算法无人机三维路径规划【含Matlab源码 168期】

一、获取代码方式

获取代码方式1：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

获取代码方式2：
完整代码已上传我的资源：【三维路径规划】基于matlab人工势场算法无人机三维路径规划【含Matlab源码 168期】

备注：
订阅紫极神光博客付费专栏，可免费获得2份代码（有效期为订阅日起，三天内有效）；

二、无人机简介

0 引言
随着现代技术的发展，飞行器种类不断变多，应用也日趋专一化、完善化，如专门用作植保的大疆PS-X625无人机，用作街景拍摄与监控巡察的宝鸡行翼航空科技的X8无人机，以及用作水下救援的白鲨MIX水下无人机等，决定飞行器性能主要是内部的飞控系统和外部的路径规划问题。就路径问题而言，在具体实施任务时仅靠操作员手中的遥控器控制无人飞行器执行相应的工作，可能会对操作员心理以及技术提出极高的要求，为了避免个人操作失误，进而造成飞行器损坏的危险，一种解决问题的方法就是对飞行器进行航迹规划。
飞行器的测量精度，航迹路径的合理规划，飞行器工作时的稳定性、安全性等这些变化对飞行器的综合控制系统要求越来越高。无人机航路规划是为了保证无人机完成特定的飞行任务，并且能够在完成任务的过程中躲避各种障碍、威胁区域而设计出最优航迹路线的问题。

1 常见的航迹规划算法

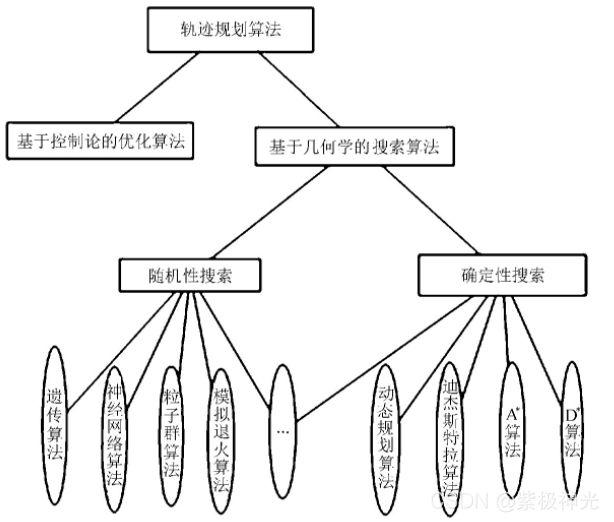
图1 常见路径规划算法
文中主要对无人机巡航阶段的航迹规划进行研究，假设无人机在飞行中维持高度与速度不变，那么航迹规划成为一个二维平面的规划问题。在航迹规划算法中,A算法计算简单，容易实现。在改进A算法基础上，提出一种新的、易于理解的改进A算法的无人机航迹规划方法。传统A算法将规划区域栅格化，节点扩展只限于栅格线的交叉点，在栅格线的交叉点与交叉点之间往往存在一定角度的两个运动方向。将存在角度的两段路径无限放大、细化，然后分别用两段上的相应路径规划点作为切点，找到相对应的组成内切圆的圆心，然后作弧，并求出相对应的两切点之间的弧所对应的圆心角，根据下式计算出弧线的长度

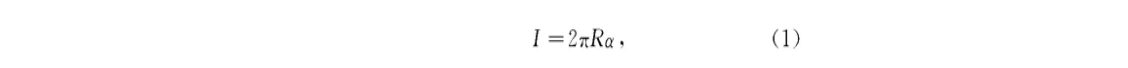
式中：R———内切圆的半径；
α———切点之间弧线对应的圆心角。

二、人工势场算法简介

人工势场算法之所以无法适应复杂的环境, 是因为斥力场系数、引力场系数在计算时是固定不变的。
1 人工势场法基本原理
人工势场法的实质是对无人机的飞行区域人为地定义势场[17], 该势场为地图中出现的障碍物斥力场和终点引力场的向量叠加。传统人工势场的定义如下:
假设无人机的位置为X= (x, y, z) , 则目标点引力场与无人机电子之间的电势场为

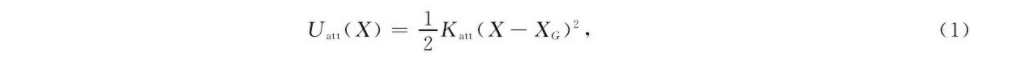
式中:Katt为势场增益系数;XG为目标点的位置。
定义Fatt (X) 为引力势场的引力,

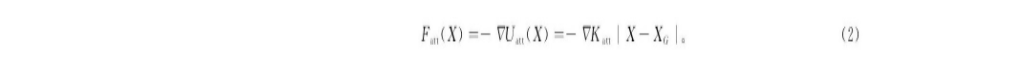
定义障碍物的斥力势场为

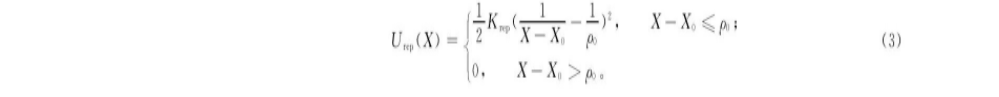
定义障碍物的斥力为

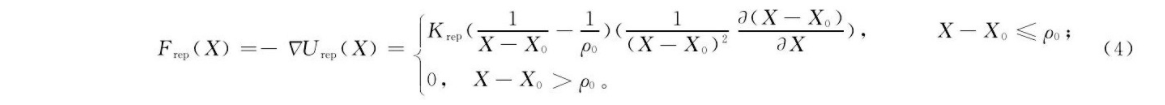
式中:Frep为障碍物对无人机的斥力势场系数;X-X0的单位是m, 表示移动的无人机到各个障碍物的动态距离;ρ0为障碍物的影响距离。所以移动的无人机像一个电子一样, 它的总势场为无人机与障碍物各个势场的和:

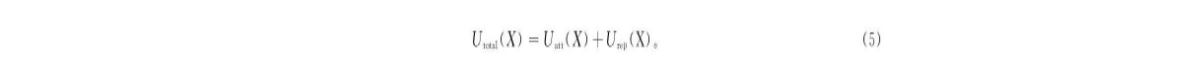
对无人机的作用力Ftotal为

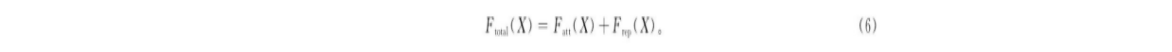
由式 (6) 可以算出无人机的下一步运动轨迹。

虽然人工势场法有很多优点, 但是在实际飞行中, 环境比较复杂的时候, 经常出现障碍物在目标位置附近的情况, 当无人机向目标点飞行时, Fatt减小Frep增大, 此时会出现无人机在终点区域拐弯的情况;当无人机处在障碍物运动时, 可能出现无人机处在合力为零点的情况, 因而无人机不能到达目标点。

三、部分源代码

close all
clear all
 
tic
%%
%==========================================================================
%初始化
%==========================================================================
P0 = [0;0;0];%起点位置
n = 7;%障碍个数
Tar = [10;10;10];%%目标点坐标
Obs = [10 10 10;1 1.2 1;3 2.5 3;4 4.5 4;3 6 3;6 2 6;6 6 6;8 8.5 8]';%目标点与障碍位置 第一列是目标点
%%
figure(1);
plot3(Obs(1,2:8),Obs(2,2:8),Obs(3,2:8),'o');hold on;
plot3(Obs(1,1),Obs(2,1),Obs(3,1),'O');
for i=1:5
    po = i;%障碍影响距离
[P,K]=shi(po,Tar,n,P0,Obs);
%==========================================================================
%画图
%==========================================================================
switch i
    case 1
plot3(P(1,1:K),P(2,1:K),P(3,1:K),'.b');
    case 2
       plot3(P(1,1:K),P(2,1:K),P(3,1:K),'.r'); 
    case 3
        plot3(P(1,1:K),P(2,1:K),P(3,1:K),'.g');
    case 4
        plot3(P(1,1:K),P(2,1:K),P(3,1:K),'.m');
        
    otherwise
        plot3(P(1,1:K),P(2,1:K),P(3,1:K),'.k');
end
end
toc

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
 

四、运行结果

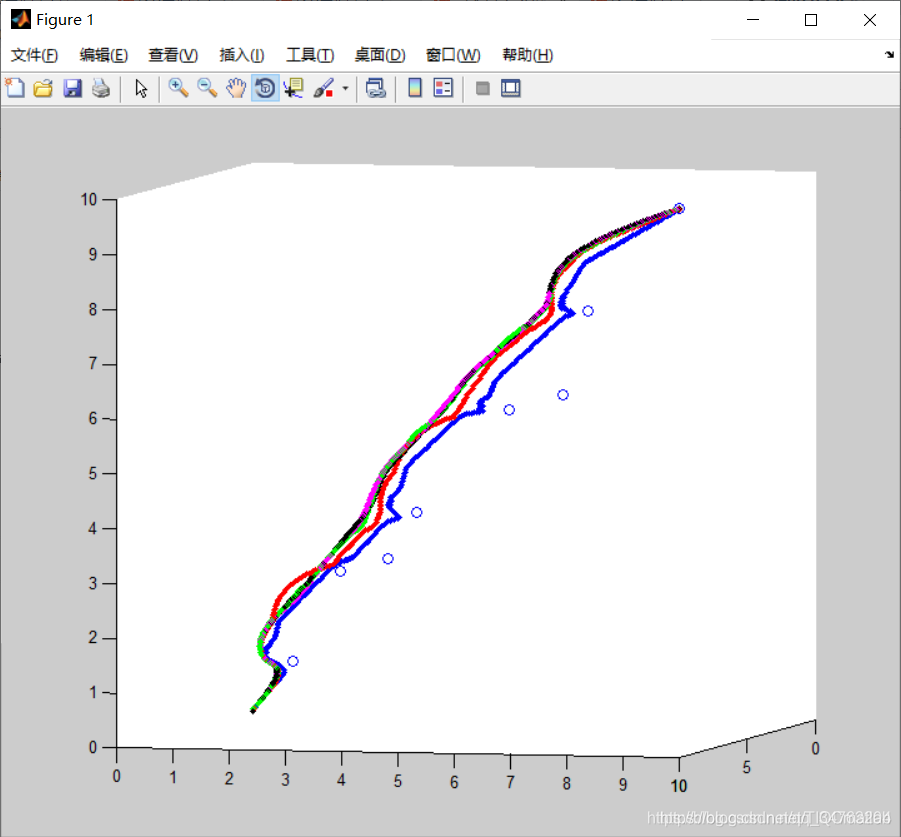
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]巫茜,罗金彪,顾晓群,曾青.基于改进PSO的无人机三维航迹规划优化算法[J].兵器装备工程学报. 2021,42(08)
[4]邓叶,姜香菊.基于改进人工势场法的四旋翼无人机航迹规划算法[J].传感器与微系统. 2021,40(07)
[5]马云红,张恒,齐乐融,贺建良.基于改进A*算法的三维无人机路径规划[J].电光与控制. 2019,26(10)
[6]焦阳.基于改进蚁群算法的无人机三维路径规划研究[J].舰船电子工程. 2019,39(03)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/113247646