【答题卡识别】基于matlab Hough变换答题卡识别【含Matlab源码 250期】

一、获取代码方式

获取代码方式1：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

获取代码方式2：
完整代码已上传我的资源：【答题卡识别】基于matlab Hough变换答题卡识别【含Matlab源码 250期】

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、答题卡识别简介

研究答题卡识别软件的设计与开发，集成了图像分割、模式识别等领域的功能模块，涉及计算机图像处理的一系列知识。通过图像处理技术，系统能够识别答题卡图像的答案选项，再通过输入正确答案的答题卡并与之对照，进而对学生答题卡进行判别并计算出分数。本案例侧重于图像识别方面的实现，应用了图像校正、模式识别等方面的算法。

1 理论基础
答题卡自动阅卷系统通过获取答题卡图像作为系统输入，并通过计算机处理、自动识别填涂标记，存入数据库完成阅卷。在图像数字化的过程中，受设备、环境等因素的影响，答题卡图像的质量在一定程度上下降，影响自动阅卷的准确率，甚至导致无法正常阅卷。因此，要对所获取的图像进行一系列的预处理，滤去干扰、噪声，做几何校正、彩色校正等操作，并进行二值化处理，以确保后续步骤能顺利进行。

1.1 图像二值化
彩色图像经过灰度化处理后得到灰度图，每个像素都仅有一个灰度值，该灰度值的大小决定了像素的亮暗程度。在答题卡自动识别实验中，根据答题卡图像答案目标的色彩特点，为了方便地进行目标答案的检测和识别，我们需要对灰度图像进行二值化处理，也就是说各像素的灰度值只有0和1两个取值，用来表示黑白两种颜色，这样可以大大减少计算的数据量。

在对答题卡图像进行二值化的过程中，阈值的选取是关键，直接影响到目标答案是否能被正确识别。根据二值化过程中的阈值选取的来源不同，阈值选取方法可以分为全局和局部两种。鉴于答题卡图像的应用场景，不同考生填涂答题卡的深浅度往往不同。如果采用由用户指定阈值的方法，则可能会产生对每张答题卡都需要进行阈值调整的要求，而且在光照不均匀等因素的影响下往往会出现目标区域二值化异常的现象。因此，在本案例中采用局部平均阈值法来自动确定阈值，当像素点的灰度值小于阈值时，则将该点的数值置为0，否则将数值置为1。该算法在不同的图像区域所选择的阈值会自动调整，也消除了光照不均匀等因素的干扰，同时在光照明暗变化时能自动调整阈值的大小。等待系统载入答题卡图像，进行灰度化化等预处理后再进行二值化，将有效突出答案目标的显示效果。

1.2 倾斜校正
在答题卡图像采集的过程中，由于种种原因，可能会导致所采集得到的答题卡图像有某种程度的倾斜，为了得到准确的阅卷结果，需要进行必要的倾斜纠正处理。答题卡图像的倾斜校正一般分为两步：第一步，查找倾斜角度；第二步，进行坐标变换，得到校正后的图像。其中， 常用的倾斜角度查找方法有两种：一种是利用Hough变换来找出倾斜角度；另一种是利用角点检测来找出倾斜角度。根据答题卡图像样式固定的特点，本案例采用Hough变换来进行倾斜角度的计算。
Hough变换作为一种参数空间变换算法， 自从1962年被Hough提出之后， 便成为直线和其他参数化形状检测的重要工具。Hough变换具有较强的稳定性和鲁棒性， 可以在一定程度上避免噪声的影响， 而且易于并行运算2。因此， Hough变换被不断地研究并取得大量进展， Duda和Halt将极坐标引入Hough变换， 使这种方法可以更加有效地用于直线检测和其他任意几何形状的检测。Ballard提出了非解析任意形状的R表法， 将Hough变换推广到对任意方向和范围的非解析任意形状的识别， 这种方法被称为广义Hough变换。
直线y=mx+b可用极坐标表示为：

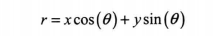
也可表示为：

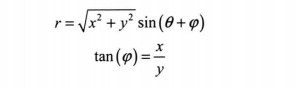
其中，1式中的(r，6)定义了一个从原点到该直线最近点的向量，显然，该向量与该直线垂直，如图所示。

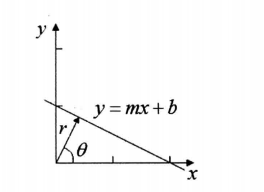
假设以参数r和0构成一个二维空间，则x、y平面上的任意一条直线对应了r、0平面上的一个点。因此， x、y平面上的任意一条直线的Hough变换就是寻找r、0平面上的一个对应点的过程。
假设x、y平面上有一个特定的点(xo，yo)，经过该点的直线可以有很多条，每一条都对应了r、0平面中的一个点，这些点必须是满足以xo、yo作为常量时的1式。因此，根据1式的定义可以发现，在参数空间与x、y空间中所有这些直线对应点的轨迹是一条正弦型曲线，即x、y平面上的任意一点对应了r、0平面上的一条正弦曲线。如果有一组位于由参数ro和0决定的直线上的边缘点，则每个边缘点对应了r、0空间的一条正弦型曲线。由于这些曲线均对应了同一条直线参数，因此所有这些曲线必交于点
(ro，0o)。
在实际计算的过程中，为了找出这些点所构成的直线段，我们可以将r、0空间进行网格化，进而将其量化成许多小格，并初始化各小格的计数累加器。根据每一个(x0，yo)点的极坐标公式，可以根据其代入0的量化值，算出各个r的值，如果经量化后的值落在某个小格内，则使该小格的计数累加器加1；当全部(x，y)点变换后，对小格计数器进行统计，包含较大计数值的小格对应于共线点，并且(r，0)可作为直线拟合参数；包含较小计数值的小格一般对应于非共线点，丢弃不用。通过以上过程可以看出，如果r、0网格量化度量过大，则其参数空间的聚合效果较差，进而很难查找直线的准确的r、0参数；同理，如果r、0网格量化度量过小，则计算量会随之增大，影响查找效率。因此，在计算过程中需要综
合考虑这两方面，选择合适的网格量化度量值2。
由于Hough变换需要进行网格扫描处理， 运行速度往往较慢， 因此在进行直线检测和倾斜角度计算时，需要考虑的一个重要因素就是计算量的问题。其中，计算量与搜索角度步长0， 和搜索角度范围0， 密切相关。因此， 采用多级Hough变换， 通过设置角度搜索步长由大到小来进行直线检测和倾斜角度计算， 可以有效降低算法的计算量。多级Hough变换首先用较大的0，和0，以求出倾斜角度的大致范围，这类似于人眼主观估计的过程。然后用较小的0，和0，对倾斜角度进行细化处理，对于某些应用场景甚至可以求出约0.02°的倾斜， 这类似于人眼仔细估计的过程。因此， 采用多级Hough变换比直接应用Hough变换在运算速度上有了较大提高。
在计算答题卡图像的倾斜角度时，为了消除涂抹区域部均匀的影响，对已获取的满足上述特征的极大值对应的倾斜角度，可采用算术平均的方式进行优化处理。假设每行答题区对应的倾斜角度为0；(i=1，2，…，N，N通常为答题区的总行数)，则图像的倾斜角度0m
由3式给出：

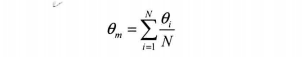
获取答题卡图像的倾斜角度后，可以对图像进行旋转处理。假设点(x.，)o)绕点(a，b)旋转0度后坐标为(x，y)，旋转后中心坐标为(c，d)，则：

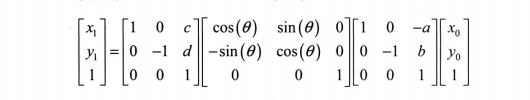
图像旋转可能会引起图像的高度和宽度范围的改变，结合答题卡图像周边区域的特点，我们对旋转图像超出范围的周边区域进行了删除处理。同时，为了尽可能保持图像的完整性，在进行旋转时以图像的中心位置作为旋转中心进行计算，对答题卡图像进行倾斜校正的效果。

1.3 图像分割
图像分割是图像处理中常用的关键步骤之一，本案例涉及对答题卡图像有效区域的检测和分割。一般情况下，对灰度图像的分割通常可基于像素灰度值的两个性质：不连续性和相似性。图像固定区域内部的像素一般都具有灰度相似性，而在不同区域之间的边界上一般具有灰度不连续性，也就是我们常说的区域边缘属性。因此，灰度图像分割方法一般可以分为基于区域的方法和基于边界的方法。前者利用区域内的灰度相似性进行分割，后者利用区域间的灰度不连续性进行分割。根据分割过程中选择的运算策略不同，分割算法又可分为并行算法和串行算法。在并行算法过程中，所有检测和分割都可独立和同时地进行，利于提高运算效率曰。在串行算法过程中，后续的处理流程要用到之前的步骤得到的结果，要求程序运行具有连续性。
基于区域的分割方法
基于区域的分割方法以区域内像素的相似性特征为依据，将图像划分成一系列有意义的独立区域，实现分割的目标。图像进行区域分割一般有以下特征。
(1)一致性。图像分割后的区域应在某些特征方面表现出一致性，如灰度、颜色或纹理。
(2)单一性。区域内部目标分布单一，不能包含太多孔洞。
(3)差异性。区域内部的同一特征在相邻区域间应有明显的差异性。
(4)准确性。区域间的分割边界应该有光滑性，且边界的空间位置准确。
基于区域的分割方法常用的有灰度阈值法和区域增长法等，其特点是充分利用了区域内像素特征的相似性。

2 程序实现
本案例提出了一种能够有效识别答题卡的方法， 利用基于Hough变换的直线检测技术检测图像的倾斜度，对存在倾斜的图像进行旋转校正，最终实现答题卡答案的定位和检测。其中，在识别过程中使用像素灰度积分统计的方法，具有较低的误识别率，能够准确定位答题卡的涂卡痕迹。下面介绍程序实现过程中的关键步骤。

2.1 图像灰度化
根据答题卡图像的自身特点，本实验要求输入的图片为灰度格式，并将采集到的答题卡图片经灰度化处理后存储到硬盘的指定文件夹，用于检测识别。采用灰度图像进行存储能显著减少文件所占用的硬盘空间，而且能提高图像处理识别的速度。一般而言，可采用加权平均值法对原始RGB图像进行灰度化处理， 该方法的主要思想是从原图像中取R、G、B各层像素值并经过加权求和得到灰度图的亮度值。现实生活中，人眼对绿色(G)敏感度最高，对红色®敏感度次之，对蓝色(B)敏感度最低，因此为了选择合适的权值对象使之能够输出合理的灰度图像，权值系数应该满足G>R>B.实验和理论证明，当R、G、B的权值系数分别为0.299、0.587和0.114时，能够得到最适合人眼观察的灰度图像。

2.2 灰度图像二值化
图像二值化是图像处理的基本技术之一，而阈值的选取则是图像二值化的关键步骤。一般而言，对于灰度图像来说，可适当选择一个或若干个灰度值T(0≤T≤255)来进行二值化，将目标和背景分开，这个灰度值T就称为阈值。因此，对于答题卡图像来说，根据考生填涂答题卡的答案目标区域特点，可选择适当的阈值T进行二值化。当像素点的灰度值小于T时，则将该点的颜色值置为“0”，否则将其颜色值置为“1”。这样就得到了只包含黑白两种颜色的二值图像。

2.3 图像平滑滤波
图像平滑滤波是一种实用的数字图像处理技术，主要是为了减少图像的噪声，常用的有中值滤波、均值滤波等方法。中值滤波指将像素邻域的灰度值进行排序后取中位数值作为中心像素的新灰度值。答题卡图像在采集过程中经常会遇到随机噪声的干扰，该噪声一般是邻域中亮度值发生随机突变的像素，并且经排序后往往出现在序列的队首或队尾，故经中值滤波后答题卡图像的随机噪声能得到有效消除。

2.4 图像校正
对答题卡图像进行校正处理主要是进行图像旋转操作，便于后续的检测和识别。图像旋转的算法很多，本实验采用的算法思路为：将需调整的答题卡图像读取到内存中，计算图像的倾斜角度，依据所得的倾斜角度旋转图像，得到校正图像。根据答题卡图像的特点，答题卡的有效信息往往位于整幅图像的特定部位，一般包括考生准考证号区域、答案区域和考试科目区域三大部分，因此对这些区域进行精确的定位即可提取图像的特征信息。答题卡图像一般由明确的矩形框和直线组成，在进行区域定位时选择Hough变换来进行直线检测， 进而获取定位信息， 计算倾斜角度， 之后进行图像旋转来得到校正结果。

2.5 填写检查
考生在涂卡时，由于种种原因可能会出现重选、漏选等错误，可根据对识别结果的影响分两种情况进行处理：一种情况是如果考生的基本信息如专业、科目、班级、学号、试卷类型等客观信息出现重选、漏选错误，则在系统识别后会立即给出错误提示，要求确认修改图像或重新采集图像；另一种情况是如果考生填涂答案时出现重选、漏选错误，则可按答案选择错误对待，并将识别结果记入存储结构。最后，系统根据事先录入的标准答案与识别存储结构进行自动评分，从而获得每名考生的考试成绩信息。
备注：此简介仅作为理论参考，与本案例实际略有出入

三、部分源代码

clc; clear all; close all;
warning off all;
I = imread('images\\1.jpg');
I1 = Image_Normalize(I, 0);
hsize = [3 3];
sigma = 0.5;
I2 = Image_Smooth(I1, hsize, sigma, 0);
I3 = Gray_Convert(I2, 0);
bw2 = Image_Binary(I3, 0);
[~, ~, xy_long] = Hough_Process(bw2, I1, 0);
angle = Compute_Angle(xy_long);
[I4, bw3] = Image_Rotate(I1, bw2, angle*1.8, 0);
[bw4, Loc1] = Morph_Process(bw3, 0);
if nargin < 3
    flag = 1;
end
[H, T, R] = hough(bw);
P = houghpeaks(H, 4, 'threshold', ceil(0.3*max(H(:))));
lines = houghlines(bw, T, R, P, 'FillGap', 50, 'MinLength', 7);
max_len = 0;
for k = 1 : length(lines)
    xy = [lines(k).point1; lines(k).point2]; 
    len = norm(lines(k).point1-lines(k).point2); 
    Len(k) = len;
    if len > max_len
        max_len = len;
        xy_long = xy;
    end
    if nargin < 5
    flag = 1;
end
Line1 = Line{1};
Line2 = Line{2};
Line3 = Line{3};
Line4 = Line{4};
yn1 = round(Line1(1, 2) + 0.18*(Line2(1, 2)-Line1(1, 2)));
yn2 = round(Line1(1, 2) + 0.34*(Line2(1, 2)-Line1(1, 2)));
yn3 = round(Line1(1, 2) + 0.50*(Line2(1, 2)-Line1(1, 2)));
Linen1_1 = [Line1(1, 1) yn1; Line1(2, 1) yn1];
Linen2_1 = [Line1(1, 1) yn2; Line1(2, 1) yn2];
Linen3_1 = [Line1(1, 1) yn3; Line1(2, 1) yn3];
% 定位竖直网格分割线
xn1 = round(Line3(1, 1) + 0.22*(Line4(1, 1)-Line3(1, 1)));
xn2 = round(Line3(1, 1) + 0.26*(Line4(1, 1)-Line3(1, 1)));
xn3 = round(Line3(1, 1) + 0.48*(Line4(1, 1)-Line3(1, 1)));
xn4 = round(Line3(1, 1) + 0.52*(Line4(1, 1)-Line3(1, 1)));
xn5 = round(Line3(1, 1) + 0.73*(Line4(1, 1)-Line3(1, 1)));
xn6 = round(Line3(1, 1) + 0.77*(Line4(1, 1)-Line3(1, 1)));
xn7 = round(Line3(1, 1) + 0.98*(Line4(1, 1)-Line3(1, 1)));

Linen1_2 = [xn1 Line3(1, 2); xn1 Line3(2, 2)];
Linen2_2 = [xn2 Line3(1, 2); xn2 Line3(2, 2)];
Linen3_2 = [xn3 Line3(1, 2); xn3 Line3(2, 2)];
Linen4_2 = [xn4 Line3(1, 2); xn4 Line3(2, 2)];
Linen5_2 = [xn5 Line3(1, 2); xn5 Line3(2, 2)];
Linen6_2 = [xn6 Line3(1, 2); xn6 Line3(2, 2)];
Linen7_2 = [xn7 Line3(1, 2); xn7 Line3(2, 2)];
ym1_1 = round(Line1(1, 2) + 0.32*(Linen1_1(1, 2)-Line1(1, 2)));
ym2_1 = round(Line1(1, 2) + 0.5*(Linen1_1(1, 2)-Line1(1, 2)));
ym3_1 = round(Line1(1, 2) + 0.65*(Linen1_1(1, 2)-Line1(1, 2)));
ym4_1 = round(Line1(1, 2) + 0.80*(Linen1_1(1, 2)-Line1(1, 2)));
ym5_1 = round(Line1(1, 2) + 0.95*(Linen1_1(1, 2)-Line1(1, 2)));
Linem1_1 = [Line1(1, 1) ym1_1; Line1(2, 1) ym1_1];
Linem2_1 = [Line1(1, 1) ym2_1; Line1(2, 1) ym2_1];
Linem3_1 = [Line1(1, 1) ym3_1; Line1(2, 1) ym3_1];
Linem4_1 = [Line1(1, 1) ym4_1; Line1(2, 1) ym4_1];
Linem5_1 = [Line1(1, 1) ym5_1; Line1(2, 1) ym5_1];

ym1_2 = round(Linen1_1(1, 2) + 0.25*(Linen2_1(1, 2)-Linen1_1(1, 2)));
ym2_2 = round(Linen1_1(1, 2) + 0.40*(Linen2_1(1, 2)-Linen1_1(1, 2)));
ym3_2 = round(Linen1_1(1, 2) + 0.60*(Linen2_1(1, 2)-Linen1_1(1, 2)));
ym4_2 = round(Linen1_1(1, 2) + 0.75*(Linen2_1(1, 2)-Linen1_1(1, 2)));
ym5_2 = round(Linen1_1(1, 2) + 0.90*(Linen2_1(1, 2)-Linen1_1(1, 2)));
Linem1_2 = [Line1(1, 1) ym1_2; Line1(2, 1) ym1_2];
Linem2_2 = [Line1(1, 1) ym2_2; Line1(2, 1) ym2_2];
Linem3_2 = [Line1(1, 1) ym3_2; Line1(2, 1) ym3_2];
Linem4_2 = [Line1(1, 1) ym4_2; Line1(2, 1) ym4_2];
Linem5_2 = [Line1(1, 1) ym5_2; Line1(2, 1) ym5_2];
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/113751323