【图像分割】基于matlab粒子群优化T熵图像分割【含Matlab源码 286期】

一、简介

本文所采用的基于熵的切割点和最小描述长度原则(MDLP)。

A.特征选择

特征选择是一个组合优化问题，因为在具有N个特征的数据集上有2N个可能的不同特征子集。FS方法通常有两个重要的部分组成，即搜索技术和特征评估方法。

在特征评估方面，FS方法通常可以分为过滤(filter)和包装(wrapper)方法。过滤法基于它们的内在特性来评估特性。过滤措施的例子有距离、信息增益、一致性和相关性。另一方面，包装法使用一种学习算法来度量所选特性的分类性能。在这个过程中可以使用不同的学习算法，比如k近邻(KNN)、决策树和支持向量机。一般来说，过滤器方法比包装器方法更快，然而，它们通常比包装器获得更低的分类精度。

在FS方法中搜索技术可以分为穷举搜索、启发式搜索、随机搜索和随机搜索。虽然穷举搜索保证找到最好的解决方案，但是由于它的计算时间太高，对大多数实际应用程序来说是不可行的。序列搜索如线性正向选择(LFS)和贪婪逐步逆向选择(GSBS)是启发式搜索的典型方法。这两种方法分别是序列正向选择(SFS)和序列逆向选择的派生版本。LFS通过限制每个步骤中考虑的特性的数量来提高SFS的有效性和效率。虽然向后选择可以考虑特性交互，而不是向前选择，但是对具有大量特性的数据集应用是不切实际的。GSBS不能在一个星期内完成，它运行在具有数百个特征的数据集上。另外，前后策略通常都要面对局部最优的问题。

随机搜索可能会以一种完全随机的方式生成子集，使用Las Vegas算法，比如LVW，在一个大的搜索空间中，它的收敛速度太慢。与随机生成不同，EC是一种随机的方法，它应用进化原理或群智能来从当前的子集生成更好的子集。PSO是一种应用于FS的群体智能技术，并显示了其有效性。大家可以通过使用EC技术对FS的不同策略进行更全面的调查。虽然PSO已经成功地应用于不同的优化问题，包括FS，但它还没有应用于离散化。

B.特征离散化

特征离散化是一个研究历史悠久的话题。在此领域提出了许多不同策略的离散化方法。但是，它们都具有相同的目的，即确定将特征值分割为离散值的分割点。在特征值的范围内，分割点或分点是真正的值，这些值被用来分割这个范围到若干个间隔。现有的离散化方法可以使用不同的标准进行分类。在直接方法中，间隔是基于预定义的参数生成的。另一方面，增量方法递归地分离(或合并)间隔，直到满足一些标准，从而产生分裂(或合并)方法。它们也被称为自顶向下或自底向上的方法。根据是否在离散化过程中使用类标签，对离散化方法进行监督或无监督。如果在每个离散化步骤中使用整个实例空间，或者如果每个离散步骤只使用一个实例子集，那么它将是全局的。一种方法也属于单变量或多变量，这取决于特征是离散的还是多个特性的离散化，同时考虑特征之间的交互。

等宽和等频是两种简单的无监督方法。它们将特性离散为一个预定义的m间隔，具有相同的宽度或相同数量的值。这些简单的方法易于实现，但对m的值敏感，通常很难确定，尤其是当特性不是均匀分布或包含异常值时。

使用类标签作为搜索切割点的引导，监督离散化通常比无监督的匹配要好。在不同的类的边界上定义了切点的特征值。除了不同的搜索技术，还有分类错误率、信息增益和统计度量等不同的评价方法。

在受监督的方法中，Fayyad和Irani提出的最小描述长度(MDL)是最常用的方法之一。它是一种基于熵的增量分割离散化方法。利用信息增益来评价候选点。MDL递归地选择最佳的切点，将一个间隔分割为两个，直到实现MDLP。受此策略启发，我们建议使用由MDLP所接受的基于熵的切点作为BBPSO的初始或候选切入点。

C.基于熵的切割点

基于熵的离散化的目的是找到最佳的分割，以便离散化的特性在类标签上尽可能的纯粹。这意味着在一个区间内的大多数值都更倾向于具有相同的类标签。如果用熵E(S)来衡量集合S的纯度，那么根据这一标准，获得最高信息增益的切点是最好的。以下公式用于计算特征A的切点T的信息增益，作为特征值的集合。S1和S2是S分区的子集。

D.通过离散化来进行特征选择

虽然FS和离散化是近几十年来新兴的领域，但是结合这些任务的方法并没有引起足够的重视。Chi2是通过离散化提出FS的第一个方法。它是一种自下而上的方法，从只有一个特征值的间隔开始。然后相邻间隔χ2最低的测试结果将合并后的递归，直到χ2值对超过一个阈值。此阈值是通过试图维护数据的预定义一致性级别来确定的。通过释放这个一致性级别，Chi2可以提出只有一个间隔的特征，可以为FS移除。结果表明，在两个合成数据集上，Chi2有效地消除了相关特征，消除了所有的噪声特征。然而，用户定义的不一致率很难预先定义，也可能导致离散化过程的不准确。改进的Chi2 (MChi2)是一种完全自动的离散化方法，解决了Chi2的缺点。

另一种通过离散化的方法是基于离散化过程中计算出的一些度量方法进行排序。然后，将选择一些级别最高的特征。这个方法的一个例子是PEAR，其中的特性是从最小的切点数量到最大的。顶级的特征被认为是相关的，并被选择形成最终的子集。结果表明，该算法具有与原特性集相似的性能，且效果较好。但是，很难为PEAR选择合适的参数，以及应该选择哪些特性来形成最终子集。同样，特征根据原始连续值的方差和用于编码离散特征的比特数的比值进行排序。

综上所述，通过离散化的特征选择在两个不同的阶段。但是，将他们整合到同一个阶段的研究目前还没有。

E.粒子群优化算法

具体可参考本人文章“计算智能(CI)之粒子群优化算法(PSO)”。本篇文章将不再赘述。

二、源代码

%%无递推
clc;
clear;
C=imread('1.jpg');
C=rgb2gray(C);
%C=imnoise(C,'gaussian',0,0.005);
figure
subplot(1,2,1)
imshow(C)
tic
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%确定基本粒子群算法的迭代次数和粒子个数
Iter =80;
global  popsize
popsize = 12;  %%粒子个数
global dimsize
dimsize=3;  %%粒子维数
 
 
%初始化基本粒子群优化算法的参数
Wmax = 0.9;             %最大惯性因子
Wmin = 0.1;             %最小惯性因子
c1 = 2.0;               %个体学习因子
c2 = 2.0;               %群体学习因子
xmax = 254;             %粒子允许的最小位置
xmin = 2; 
speedmax=10;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    gBest
     toc 
    % t=toc-tic;
    %写入最终结果图
    [m,n]=size(C);
   z=zeros(m,n); 
% percentege=0;
    for i=1:m
        for j=1:n
          if C(i,j)<=round(gBest(1))-1
           z(i,j)=0; 
          elseif C(i,j)<=round(gBest(2))-1
              z(i,j)=75;
          elseif C(i,j)<=round(gBest(3))-1
              z(i,j)=175;
          else
              z(i,j)=255;
    %           percentege=percentege+1;
          end
      end
    end
    z=z/255;
    subplot(1,2,2);
    imshow(z);
              

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
 

三、运行结果

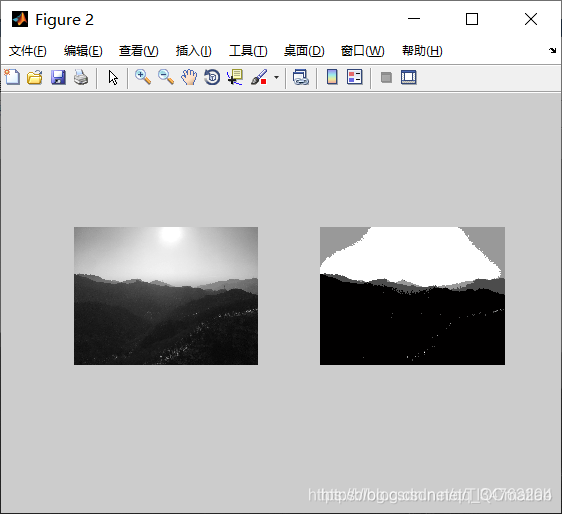
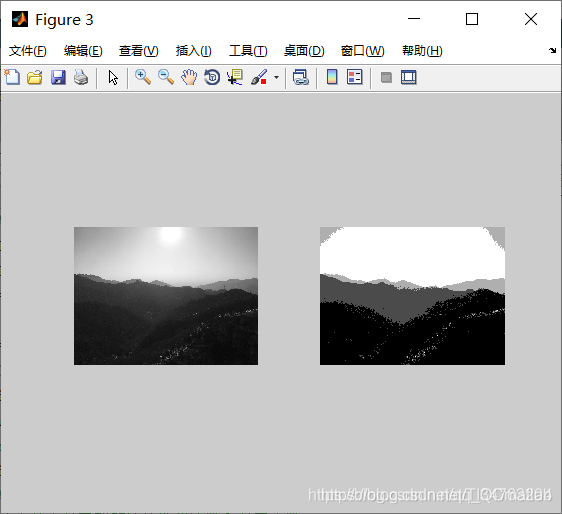
四、备注

版本：2014a

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/113797475