【背包问题】基于matlab离散粒子群算法求解背包问题【含Matlab源码 423期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源： 【背包问题】基于matlab离散粒子群算法求解背包问题【含Matlab源码 423期】

二、背包问题简介

1【背包问题】
背包问题(Knapsack problem)是一种组合优化的NP完全问题。
问题描述为：给定一组物品，每种物品都有自己的重量weight和价格value，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。
2【0-1背包问题】
对每个物品i 只有 装入/不装入背包 两种情况。
我们有n种物品，物品j的重量为wj，价格为pj。
我们假定所有物品的重量和价格都是非负的。背包所能承受的最大重量为W。
如果限定每种物品只能选择0个或1个，则问题称为0-1背包问题。
令V（i，j）表示前i个物品中能够装入容量为j的背包中的物品价值最大值，则可得到动态规划函数：
V(i,0) = V(0,j)=0; //把前i个物品装入容量为0的背包 和 把0个物品装入容量为j的背包，价值均为0
V(i,j) = V(i-1,j) j<wi //如果第i个物品的重量大于背包容量wi>j，则装入前i个物品得到的最大价值和装入前i-1个物品得到的最大价值相同，即物品i不装入背包
V(i,j) = max{ V(i-1,j)，V(i-1,j-wi)+vi } j>wi // 1.如果把第i个物品装入背包，则背包中物品的价值=把前i-1个物品装入容量为j-wi背包中的价值加上第i个物品的价值vi； 2. 如果第i个物品没有装入背包，则背包中价值=前i-1个物品装入容量为j的背包中所取得的价值。 取二者中价值较大者。
step 1：只装入前1个物品，确定各种情况下的背包能够得到的最大价值；
step 2：只装人前2个物品，确定各种情况下的背包能够得到的最大价值；.
step n：…
最后V(n,C)便是容量为C的背包中装入n个物品时取得的最大价值。
为了得到V(n,C) 需想前推到V(n-1,C)。如果V(n,C)>V(n-1,C),则第n个物品装入背包，前n-1个物品装入容量为C-wn的背包中；否则，第n个物品没有被装入背包，前n-1个物品被装入容量为C的背包中。
直到确定第一个物品是否被装入背包中。
得到：
当 V(i,j)= V(i-1,j)， xi = 0；
当 V(i,j) > V(i-1,j)， xi = 1，j = j-wi；

三、离散粒子群算法简介

1 什么是离散粒子群算法？
普通粒子群算法（Particle Swarm Optimization Algorithm，PSO）的粒子初始位置、更新速度都是连续函数，与之对应，位置和速度更新均为离散值的算法是离散PSO算法（Discrete Particle Swarm Optimization Algorithm， DPSO）；
一般就是在跟新粒子位置后，对粒子进行离散点处理；
比如：你的粒子的离散点是0到9的整数。那么对每个粒子更新位置后，比如是在（0,1）范围内的随机数。那么就（0，0.1）范围令其值为0；（0.1,0.2）范围令其值为1；…（0.9.1）范围令其值为9。当然初始位置值也需要这样处理。参考

2 什么是离散二进制粒子群算法？
离散二进制粒子群算法（Discrete Binary Particle Swarm Optimization Algorithm， BPSO）最初由J.Kennedy和R.C.Eberhart在1997年设计;
PSO主要优化连续实值问题，BPSO主要优化离散空间约束问题；
BPSO是在离散粒子群算法基础上，约定位置向量、速度向量均由0、1值构成；
BPSO有很强全局搜索能力，但不能收敛于全局最优值，且随着算法迭代搜索随机性越来越强，缺乏后期的局部搜索能力；

3 离散二进制粒子群算法步骤




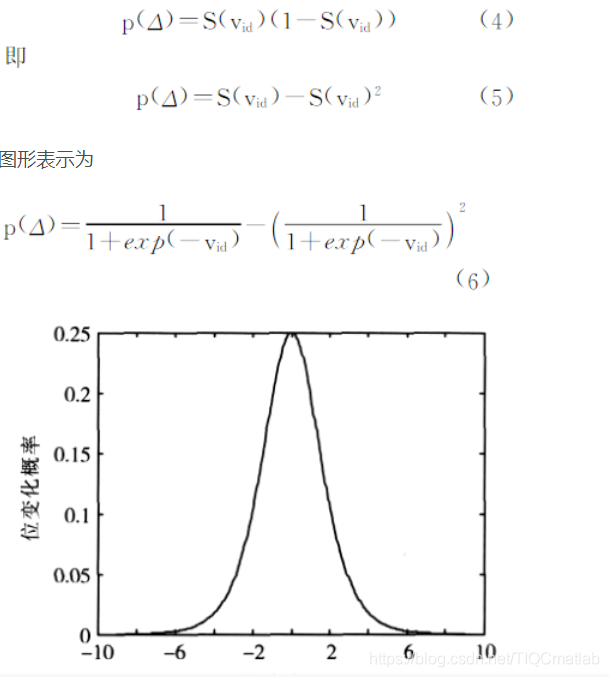
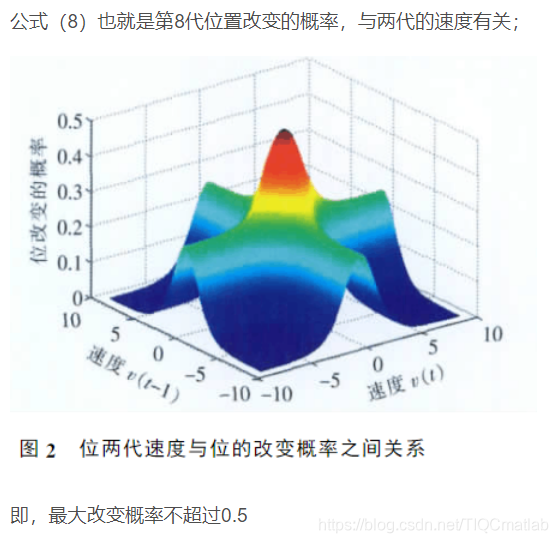
4 实验步骤
参考：离散二进制粒子群算法分析
第一步：确定测试的基准函数；
第二步：测试某个粒子的平均速度迭代变化，某个粒子取1的平均概率迭代变化；某个粒子改变概率迭代变化；某个粒子到最优粒子距离的迭代变化；
第三步：提出改进的粒子群算法，改进点为概率函数；按照第二步进行实验；
第四步：提出改进的基于遗传算法的二进制PSO算法；进行显著性分析，测试最小平均适应度值和标准方差；

四、部分源代码

clear all;
%------给定初始化条件---------------------------------------------- 
c1=2;            %学习因子1 
c2=2;             %学习因子2 
w=0.7298;            %惯性权重 
MaxDT=1000;          %最大迭代次数 
D=10;                 %搜索空间维数（未知数个数） 
N=50;                  %初始化群体个体数目 
c=[55,10,47,5,4,50,8,61,85,87]; %价格
a=[95,4,60,32,23,72,80,62,65,46];  %体积
b=269;  %总体积
% % 100
% c=[297,295,293,292, 291,289,284,284,283,283,281,280,279,277,276,275,273,264,260, 257,250,236,236,235,235,233,232,232,228,218,217,214,211,208, 205,204,203,201,196,194,193,193,192,191,190,187,187,184,184, 184,181,179,176,173,172,171,160,128,123,114,113,107,105,101, 100,100,99,98,97,94,94,93,91,80,74,73,72,63,63,62,61,60,56,53, 52,50,48,46,40,40,35,28,22,22,18,15,12,11,6,5];
% a=[54,95,36,18,4,71,83,16,27,84,88,45,94,64,14,80,4,23,75,36, 90,20,77,32,58,6,14,86,84,59,71,21,30,22,96,49,81,48,37,28,6, 84,19,55,88,38,51,52,79,55,70,53,64,99,61,86,1,64,32,60,42,45, 34,22,49,37,33,1,78,43,85,24,96,32,99,57,23,8,10,74,59,89,95,40, 46,65,6,89,84,83,6,19,45,59,26,13,8,26,5,9];
% b=3820;
% % 80
% c=[199,194,193,191, 189,178,174,169,164,164,161,158,157,154,152,152,149,142,131, 125,124,124,124,122,119,116,114,113,111,110,109,100,97,94, 91,82, 82,81,80,80,80, 79,77,76,74,72,71,70,69,68,65,65,61, 56,55, 54,53,47,47,46,41,36,34,32,32,30,29,29,26,25,23,22,20,11,10,9,5, 4,3,1];
% a=[40,27,5,21,51,16,42,18,52,28,57,34, 44,43,52,55,53,42,47,56,57,44,16,2,12,9,40,23,56,3,39,16,54,36, 52,5,53,48,23,47,41,49,22,42,10,16,53,58,40,1,43,56,40,32,44,35, 37,45,52,56,40,2,23,49,50,26,11,35,32,34,58,6,52,26,31,23,4,52,53,19];
% b=1173;
% 50
% c=[293,291,290,280, 278,274,269,265,248,247,245,245,241,234,229,228,222,216,214,191,191,187,171,170,164,152,142,132,131,126,122,116,112,111,110,106,77,76,74,73,69,67,42,41,35,33,30,29,28,26]; %价格
% a=[95,39,69,63,49,104,56,58,47,23,17,129,91,28,77,125,73, 5,103,63,76,23,47,79,119,125,26,119,79,56,50,75,12,26,31,43,41,38,29,21,14,9,3,17,8,8,9,7,4,5];  %体积
% b=959;  %总体积
% % 20
% c=[44, 46, 90, 72, 91, 40, 75, 35, 8, 54, 78, 40, 77, 15, 61, 17, 75, 29, 75, 63]; %价格
% a=[92, 4, 43, 83, 84, 68, 92, 82, 6, 44, 32, 18, 56, 83, 25, 96, 70, 48, 14, 58];  %体积
% b=878;  %总体积


%------初始化种群的个体------------ 
x=zeros(N,D);
for i=1:N,
    for j=1:D % For dimension
        if rand<=0.5
            x(i,j)=0;
        else
            x(i,j)=1;
        end
    end
end
p=x;
v(1,:)=0.1*x(1,:);
for i=1:N
    if a*x(i,:)'>b
        x(i,:)=GTA( x(i,:),c,a,b );
    end
end
pg=x(1,:);
%------主循环------------ 
for t=1:MaxDT 
    for i=2:N 
        
        for j=1:D
        v(i,j)=w*v(i-1,j )+c1*round(rand(1))*(p(i-1,j)-x(i-1,j))+c2*round(rand(1))*(pg(1,j)-x(i-1,j));
        q=rand(1);
        if [1/(1+exp(-x(i,j)))]>q
            x(i,j)=1;
        else x(i,j)=0;
        end  
        end
        
        if a*x(i,:)'>b
            x(i,:)=GTA( x(i,:),c,a,b );
        end
        
        if c*(x(i,:))'>c*(p(i-1,:))'
        	p(i,:)=x(i,:);
        else p(i,:)=p(i-1,:);
        end
        
     
        %
        if c*(p(i,:))'>c*(pg)'
            pg=p(i,:);      
        end
    end
    %------初始化种群的个体------------ 
x=eye(N,D);
p=x;
v(1,:)=0.1*x(1,:);
pg=x(1,:);
%------主循环------------ 
for t=1:MaxDT 
    for i=2:N 
        
        for j=1:D
        v(i,j)=w*v(i-1,j )+c1*round(rand(1))*(p(i-1,j)-x(i-1,j))+c2*round(rand(1))*(pg(1,j)-x(i-1,j));
        q=rand(1);
        if [1/(1+exp(-v(i,j)))]>q
            x(i,j)=1;
        else x(i,j)=0;
        end  
        end
        
        if a*x(i,:)'<b
            if c*(x(i,:))'>c*(p(i-1,:))'
                p(i,:)=x(i,:);
            else p(i,:)=p(i-1,:);
            end
        else p(i,:)=p(i-1,:);
        end
     
        %
        if c*(p(i,:))'>c*(pg)'
            pg=p(i,:);      
        end
    end

  

五、运行结果

六、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/114223310