【路径规划】基于matlab改进的粒子群算法路径规划【含Matlab源码 491期】

一、粒子群算法简介

1 引言
自然界中的鸟群和鱼群的群体行为一直是科学家的研究兴趣所在。生物学家Craig Reynolds在1987年提出了一个非常有影响的鸟群聚集模型，在他的仿真中，每一个个体都遵循：避免与邻域个体相撞：匹配邻域个体的速度；飞向鸟群中心，且整个群体飞向目标。仿真中仅利用上面三条简单的规则，就可以非常接近地模拟出鸟群飞行的现象。1990年， 生物学家Frank Heppner也提出了鸟类模型， 它的不同之处在于：鸟类被吸引飞到栖息地。在仿真中，一开始每一只鸟都没有特定的飞行目标，只是使用简单的规则确定自己的飞行方向和飞行速度，当有一只鸟飞到栖息地时，它周围的鸟也会跟着飞向栖息地，最终整个鸟群都会落在栖息地。
1995年， 美国社会心理学家James Kennedy和电气工程师RussellEberhart共同提出了粒子群算法(ParticleS warm Optimization， PSO) ， 该算法的提出是受对鸟类群体行为进行建模与仿真的研究结果的启发。他们的模型和仿真算法主要对Frank Heppner的模型进行了修正，以使粒子飞向解空间并在最优解处降落。粒子群算法一经提出，由于其算法简单，容易实现，立刻引起了进化计算领域学者们的广泛关注， 形成一个研究热点。2001年出版的J.Kennedy与R.Eberhart合著的《群体智能》将群体智能的影响进一步扩大[] ， 随后关于粒子群优化算法的研究报告和研究成果大量涌现，继而掀起了国内外研究热潮[2-7]。
粒子群优化算法来源于鸟类群体活动的规律性，进而利用群体智能建立一个简化的模型。它模拟鸟类的觅食行为，将求解问题的搜索空间比作鸟类的飞行空间，将每只鸟抽象成一个没有质量和体积的粒
子，用它来表征问题的一个可能解，将寻找问题最优解的过程看成鸟类寻找食物的过程，进而求解复杂的优化问题。粒子群优化算法与其他进化算法一样，也是基于“种群”和“进化”的概念，通过个体间
的协作与竞争，实现复杂空间最优解的搜索。同时，它又不像其他进化算法那样对个体进行交叉、变异、选择等进化算子操作，而是将群体中的个体看作在l维搜索空间中没有质量和体积的粒子，每个粒子以一定的速度在解空间运动， 并向自身历史最佳位置P best和邻域历史最佳位置g best聚集， 实现对候选解的进化。粒子群算法具有很好的生物社会背景而易于理解，由于参数少而容易实现，对非线性、多峰问题均具有较强的全局搜索能力，在科学研究与工程实践中得到了广泛关注。目前，该算法已广泛应用于函数优化、神经网络训练、模式分类、模糊控制等领域。

2 粒子群算法理论
2.1粒子群算法描述
鸟类在捕食过程中，鸟群成员可以通过个体之间的信息交流与共享获得其他成员的发现与飞行经历。在食物源零星分布并且不可预测的条件下，这种协作机制所带来的优势是决定性的，远远大于对食物
的竞争所引起的劣势。粒子群算法受鸟类捕食行为的启发并对这种行为进行模仿，将优化问题的搜索空间类比于鸟类的飞行空间，将每只鸟抽象为一个粒子，粒子无质量、无体积，用以表征问题的一个可行解，优化问题所要搜索到的最优解则等同于鸟类寻找的食物源。粒子群算法为每个粒子制定了与鸟类运动类似的简单行为规则，使整个粒子群的运动表现出与鸟类捕食相似的特性，从而可以求解复杂的优化问题。
粒子群算法的信息共享机制可以解释为一种共生合作的行为，即每个粒子都在不停地进行搜索，并且其搜索行为在不同程度上受到群体中其他个体的影响[8]，同时这些粒子还具备对所经历最佳位置的记
忆能力，即其搜索行为在受其他个体影响的同时还受到自身经验的引导。基于独特的搜索机制，粒子群算法首先生成初始种群，即在可行解空间和速度空间随机初始化粒子的速度与位置，其中粒子的位置用于表征问题的可行解，然后通过种群间粒子个体的合作与竞争来求解优化问题。
2.2粒子群算法建模
粒子群优化算法源自对鸟群捕食行为的研究：一群鸟在区域中随机搜索食物，所有鸟知道自己当前位置离食物多远，那么搜索的最简单有效的策略就是搜寻目前离食物最近的鸟的周围区域。粒子群算法
利用这种模型得到启示并应用于解决优化问题。在粒子群算法中，每个优化问题的潜在解都是搜索空间中的一只鸟，称之为粒子。所有的粒子都有一个由被优化的函数决定的适应度值，每个粒子还有一个速度决定它们飞翔的方向和距离。然后，粒子们就追随当前的最优粒子在解空间中搜索[9]。

粒子群算法首先在给定的解空间中随机初始化粒子群，待优化问题的变量数决定了解空间的维数。每个粒子有了初始位置与初始速度，然后通过迭代寻优。在每一次迭代中，每个粒子通过跟踪两个“极值”来更新自己在解空间中的空间位置与飞行速度：一个极值就是单个粒子本身在迭代过程中找到的最优解粒子，这个粒子叫作个体极值：另一个极值是种群所有粒子在迭代过程中所找到的最优解粒子，这个粒子是全局极值。上述的方法叫作全局粒子群算法。如果不用种群所有粒子而只用其中一部分作为该粒子的邻居粒子，那么在所有邻居粒子中的极值就是局部极值，该方法称为局部粒子群算法。

2.3粒子群算法的特点
粒子群算法本质是一种随机搜索算法，它是一种新兴的智能优化技术。该算法能以较大概率收敛于全局最优解。实践证明，它适合在动态、多目标优化环境中寻优，与传统优化算法相比，具有较快的计
算速度和更好的全局搜索能力。
(1)粒子群算法是基于群智能理论的优化算法，通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索。与其他算法相比，粒子群算法是一种高效的并行搜索算法。
(2)粒子群算法与遗传算法都是随机初始化种群，使用适应值来评价个体的优劣程度和进行一定的随机搜索。但粒子群算法根据自己的速度来决定搜索，没有遗传算法的交叉与变异。与进化算法相比，粒子群算法保留了基于种群的全局搜索策略，但是其采用的速度-位移模型操作简单，避免了复杂的遗传操作。
(3)由于每个粒子在算法结束时仍保持其个体极值，即粒子群算法除了可以找到问题的最优解外，还会得到若干较好的次优解，因此将粒子群算法用于调度和决策问题可以给出多种有意义的方案。
(4)粒子群算法特有的记忆使其可以动态地跟踪当前搜索情况并调整其搜索策略。另外，粒子群算法对种群的大小不敏感，即使种群数目下降时，性能下降也不是很大。

3 粒子群算法种类
3.1基本粒子群算法

3.2标准粒子群算法
引入研究粒子群算法经常用到的两个概念：一是“探索”，指粒子在一定程度上离开原先的搜索轨迹，向新的方向进行搜索，体现了一种向未知区域开拓的能力，类似于全局搜索；二是“开发”，指粒子在一定程度上继续在原先的搜索轨迹上进行更细一步的搜索，主要指对探索过程中所搜索到的区域进行更进一步的搜索。探索是偏离原来的寻优轨迹去寻找一个更好的解，探索能力是一个算法的全局搜索能力。开发是利用一个好的解，继续原来的寻优轨迹去搜索更好的解，它是算法的局部搜索能力。如何确定局部搜索能力和全局搜索能力的比例， 对一个问题的求解过程很重要。1998年， Shi Yuhui等人提出了带有惯性权重的改进粒子群算法[10]，由于该算法能够保证较好的收敛效果，所以被默认为标准粒子群算法。其进化过程为：

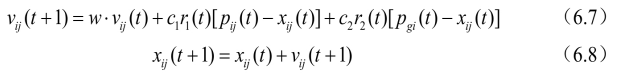
在式(6.7)中，第一部分表示粒子先前的速度，用于保证算法的全局收敛性能；第二部分、第三部分则使算法具有局部收敛能力。可以看出，式(6.7)中惯性权重w表示在多大程度上保留原来的速度：W
较大，则全局收敛能力较强，局部收敛能力较弱；w较小，则局部收敛能力较强，全局收敛能力较弱。
当w=1时，式(6.7)与式(6.5)完全一样，表明带惯性权重的粒子群算法是基本粒子群算法的扩展。实验结果表明：w在0.8~1.2之间时，粒子群算法有更快的收敛速度；而当w>1.2时，算法则容易陷入局部极值。
另外，在搜索过程中可以对w进行动态调整：在算法开始时，可给w赋予较大正值，随着搜索的进行，可以线性地使w逐渐减小，这样可以保证在算法开始时，各粒子能够以较大的速度步长在全局范围内探
测到较好的区域；而在搜索后期，较小的w值则保证粒子能够在极值点周围做精细的搜索，从而使算法有较大的概率向全局最优解位置收敛。对w进行调整，可以权衡全局搜索和局部搜索能力。目前，采用较多的动态惯性权重值是Shi提出的线性递减权值策略， 其表达式如下：

3.3压缩因子粒子群算法
Clerc等人提出利用约束因子来控制系统行为的最终收敛[11] ， 该方法可以有效搜索不同的区域，并且能得到高质量的解。压缩因子法的速度更新公式为：

实验结果表明：与使用惯性权重的粒子群优化算法相比，使用具
有约束因子的粒子群算法具有更快的收敛速度。
3.4离散粒子群算法
基本的粒子群算法是在连续域中搜索函数极值的有力工具。继基本粒子群算法之后， Kennedy和Eberhart又提出了一种离散二进制版的粒子群算法[12]。在此离散粒子群方法中，将离散问题空间映射到连续粒子运动空间，并适当修改粒子群算法来求解，在计算上仍保留经典粒子群算法速度-位置更新运算规则。粒子在状态空间的取值和变化只限于0和1两个值， 而速度的每一维vi y代表位置每一位xi取值为1的可能性。因此， 在连续粒子群中的vij更新公式依然保持不变， 但是P best和：best只在[0， 1] 内取值。其位置更新等式表示如下：

4 粒子群算法流程
粒子群算法基于“种群”和“进化”的概念，通过个体间的协作与竞争，实现复杂空间最优解的搜索[13]，其流程如下：
(1)初始化粒子群，包括群体规模N，每个粒子的位置x；和速度Vio
(2) 计算每个粒子的适应度值fit[i] 。
(3) 对每个粒子， 用它的适应度值fit[门和个体极值P best(i)比较。如果fit[i] <P best(i) ， 则用fit[i] 替换掉P best(i) 。
(4) 对每个粒子， 用它的适应度值fit[i] 和全局极值g best比较。如果fit[i] < 8 best， 则用fit[i] 替换g best。
(5)迭代更新粒子的速度v；和位置xj。
(6)进行边界条件处理。
(7)判断算法终止条件是否满足：若是，则结束算法并输出优化结果；否则返回步骤(2)。
粒子群算法的运算流程如图6.1所示。

5 关键参数说明
在粒子群优化算法中，控制参数的选择能够影响算法的性能和效率；如何选择合适的控制参数使算法性能最佳，是一个复杂的优化问题。在实际的优化问题中，通常根据使用者的经验来选取控制参数。
粒子群算法的控制参数主要包括：粒子种群规模N，惯性权重w，加速系数c和c， 最大速度Via x， 停止准则， 邻域结构的设定， 边界条件处理策略等[14]，
粒子种群规模N
粒子种群大小的选择视具体问题而定，但是一般设置粒子数为20~50。对于大部分的问题10个粒子，已经可以取得很好的结果：不过对于比较难的问题或者特定类型的问题，粒子的数量可以取到100或
200。另外，粒子数目越大，算法搜索的空间范围就越大，也就更容易发现全局最优解；当然，算法运行的时间也越长。
惯性权重w
惯性权重w是标准粒子群算法中非常重要的控制参数，可以用来控制算法的开发和探索能力。惯性权重的大小表示了对粒子当前速度继承的多少。当惯性权重值较大时，全局寻优能力较强，局部寻优能力
较弱：当惯性权重值较小时，全局寻优能力较弱，局部寻优能力较强。惯性权重的选择通常有固定权重和时变权重。固定权重就是选择常数作为惯性权重值，在进化过程中其值保持不变，一般取值为
[0.8，1.2]：时变权重则是设定某一变化区间，在进化过程中按照某种方式逐步减小惯性权重。时变权重的选择包括变化范围和递减率。固定的惯性权重可以使粒子保持相同的探索和开发能力，而时变权重可以使粒子在进化的不同阶段拥有不同的探索和开发能力。
加速常数c1和c2
加速常数c和c 2分别调节向P best和g best方向飞行的最大步长， 它们分别决定粒子个体经验和群体经验对粒子运行轨迹的影响，反映粒子群之间的信息交流。如果cr=c2=0，则粒子将以当前的飞行速度飞到边界。此时，粒子仅能搜索有限的区域，所以难以找到最优解。如果q=0，则为“社会”模型，粒子缺乏认知能力，而只有群体经验，它的收敛速度较快，但容易陷入局部最优；如果oy=0，则为“认知”模
型，没有社会的共享信息，个体之间没有信息的交互，所以找到最优解的概率较小，一个规模为D的群体等价于运行了N个各行其是的粒子。因此一般设置c1=C2，通常可以取c1=cg=1.5。这样，个体经验和群体经验就有了同样重要的影响力，使得最后的最优解更精确。
粒子的最大速度vmax
粒子的速度在空间中的每一维上都有一个最大速度限制值vd max，用来对粒子的速度进行钳制， 使速度控制在范围[-Vimax， +va max] 内，这决定问题空间搜索的力度， 该值一般由用户自己设定。Vmax是一个非常重要的参数，如果该值太大，则粒子们也许会飞过优秀区域：而如果该值太小，则粒子们可能无法对局部最优区域以外的区域进行充分的探测。它们可能会陷入局部最优，而无法移动足够远的距离而跳出局部最优， 达到空间中更佳的位置。研究者指出， 设定Vmax和调整惯性权重的作用是等效的， 所以!max一般用于对种群的初始化进行设定， 即将vmax设定为每维变量的变化范围， 而不再对最大速度进行细致的选择和调节。
停止准则
最大迭代次数、计算精度或最优解的最大停滞步数▲t(或可以接受的满意解)通常认为是停止准则，即算法的终止条件。根据具体的优化问题，停止准则的设定需同时兼顾算法的求解时间、优化质量和
搜索效率等多方面性能。
邻域结构的设定
全局版本的粒子群算法将整个群体作为粒子的邻域，具有收敛速度快的优点，但有时算法会陷入局部最优。局部版本的粒子群算法将位置相近的个体作为粒子的邻域，收敛速度较慢，不易陷入局部最优
值。实际应用中，可先采用全局粒子群算法寻找最优解的方向，即得到大致的结果，然后采用局部粒子群算法在最优点附近进行精细搜索。
边界条件处理
当某一维或若干维的位置或速度超过设定值时，采用边界条件处理策略可将粒子的位置限制在可行搜索空间内，这样能避免种群的膨胀与发散，也能避免粒子大范围地盲目搜索，从而提高了搜索效率。
具体的方法有很多种， 比如通过设置最大位置限制Xmax和最大速度限制Vmax， 当超过最大位置或最大速度时， 在范围内随机产生一个数值代替，或者将其设置为最大值，即边界吸收。

二、部分源代码

function [xOpt,fval,exitflag,output,population,scores] = ...
    pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq,LB,UB,nonlcon,options)
% Find the minimum of a function using Particle Swarm Optimization.
%
% This is an implementation of Particle Swarm Optimization algorithm using
% the same syntax as the Genetic Algorithm Toolbox, with some additional
% options specific to PSO. Allows code-reusability when trying different
% population-based optimization algorithms. Certain GA-specific parameters
% such as cross-over and mutation functions will not be applicable to the
% PSO algorithm. Demo function included, with a small library of test
% functions. Requires Optimization Toolbox.
%
% New features will be added regularly until this is made redundant by an
% official MATLAB PSO toolbox.
%
% Author: S. Samuel Chen. Version 1.31.2.
% Available from http://www.mathworks.com/matlabcentral/fileexchange/25986
% Distributed under BSD license. First published in 2009.
%
% Syntax:
% psodemo
% pso
% x = pso(fitnessfcn,nvars)
% x = pso(fitnessfcn,nvars,Aineq,bineq)
% x = pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq)
% x = pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq,LB,UB)
% x = pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq,LB,UB,nonlcon)
% x = pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq,LB,UB,nonlcon,options)
% x = pso(problem)
% [x, fval] = pso(...)
% [x, fval,exitflag] = pso(...)
% [x, fval,exitflag,output] = pso(...)
% [x, fval,exitflag,output,population] = pso(...)
% [x, fval,exitflag,output,population,scores] = pso(...)
%
% Description:
% psodemo
% Runs a demonstration of the PSO algorithm using test function specified
% by user.
%
% pso
% Runs a default demonstration using Rosenbrock's banana function.
%
% x = pso(fitnessfcn,nvars)
% Runs the particle swarm algorithm with no constraints and default
% options. fitnessfcn is a function handle, nvars is the number of
% parameters to be optimized, i.e. the dimensionality of the problem. x is
% a 1xnvars vector representing the coordinates of the global optimum
% found by the pso algorithm.
%
% x = pso(fitnessfcn,nvars,Aineq,bineq)
% Linear constraints, such that Aineq*x <= bineq. Aineq is a matrix of size
% nconstraints x nvars, while b is a column vector of length nvars.
%
% x = pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq)
% Linear equality constraints, such that Aeq*x = beq. 'Soft' or 'penalize'
% boundaries only. If no inequality constraints exist, set Aineq and bineq
% to [].
%
% x = pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq,LB,UB)
% Lower and upper bounds defined as LB and UB respectively. Both LB and UB,
% if defined, should be 1 x nvars vectors. Use empty arrays [] for Aineq,
% bineq, Aeq, or beq if no linear constraints exist.
%
% x = pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq,LB,UB,nonlcon)
% Non-linear constraints. Nonlinear inequality constraints in the form c(x)
% <= 0 have now been implemented using 'soft' boundaries, or
% experimentally, using 'penalize' constraint handling method. See the
% Optimization Toolbox documentation for the proper syntax for defining
% nonlinear constraints. Use empty arrays [] for Aineq, bineq, Aeq, beq,
% LB, or UB if they are not needed.
%
% x = pso(fitnessfcn,nvars,Aineq,bineq,Aeq,beq,LB,UB,nonlcon,options)
% Default algorithm parameters replaced with those defined in the options
% structure:
% Use >> options = psooptimset('Param1,'value1','Param2,'value2',...) to
% generate the options structure. Type >> psooptimset with no input or
% output arguments to display a list of available options and their
% default values.
%
% NOTE: the swarm will perform better if the PopInitRange option is defined
% so that it closely bounds the expected domain of the feasible region.
% This is automatically done if the problem has both lower and upper bound
% constraints, but not for linear and nonlinear constraints.
%
% NOTE 2: If options.HybridFcn is to be defined, and if it is necessary to
% pass a non-default options structure to the hybrid function, then the
% options structure may be included in a cell array along with the pointer
% to the hybrid function. Example:
% >> % Let's say that we want to use fmincon to refine the result from PSO:
% >> hybridoptions = optimset(@fmincon) ;
% >> options.HybridFcn = {@fmincon, hybridoptions} ;
%
% NOTE 3:
% Perez and Behdinan (2007) demonstrated that the particle swarm is only
% stable if the following conditions are satisfied:
% Given that C0 = particle inertia
%            C1 = options.SocialAttraction
%            C2 = options.CognitiveAttraction
%    1) 0 < (C1 + C2) < 4
%    2) (C1 + C2)/2 - 1 < C0 < 1
% If conditions 1 and 2 are satisfied, the system will be guaranteed to
% converge to a stable equilibrium point. However, whether or not this
% point is actually the global minimum cannot be guaranteed, and its
% acceptability as a solution should be verified by the user.
%
% x = pso(problem)
% Parameters imported from problem structure.
%
% [x,fval] = pso(...)
% Returns the fitness value of the best solution.
%
% [x,fval,exitflag] = pso(...)
% Returns information on outcome of pso run. This should match exitflag
% values for GA where applicable, for code reuseability between the two
% toolboxes.
%
% [x,fval,exitflag,output] = pso(...)
% The structure output contains more detailed information about the PSO
% run. It should match output fields of GA, where applicable.
%
% [x,fval,exitflag,output,population] = pso(...)
% A matrix population of size PopulationSize x nvars, with the locations of
% particles across the rows. This may be used to save the final positions
% of all the particles in a swarm.
%
% [x,fval,exitflag,output,population,scores] = pso(...)
% Final scores of the particles in population.
%
% Bibliography
% J Kennedy, RC Eberhart, YH Shi. Swarm Intelligence. Academic Press, 2001.
%
% SM Mikki, AA Kishk. Particle Swarm Optimization: A Physics-Based
% Approach. Morgan & Claypool, 2008.
%
% RE Perez and K Behdinan. "Particle swarm approach for structural
% design optimization." Computers and Structures, Vol. 85:1579-88, 2007.
%
% See also:
% PSODEMO, PSOOPTIMSET, PSOBINARY.

if ~nargin % Rosenbrock's banana function by default, as a demonstration
    fitnessfcn = @(x)100*(x(2)-x(1)^2)^2+(1-x(1))^2 ;
    nvars = 2 ;
    LB = [-1.5,-2] ;
    UB = [2,2] ;
    options.PopInitRange = [[-2;4],[-1;2]] ;
    options.PlotFcns = {@psoplotbestf,@psoplotswarmsurf} ;
    options.Generations = 200 ;
    options.DemoMode = 'on' ;
    options.KnownMin = [1 1] ;
    options.OutputFcns = {} ;
    options.ConstrBoundary = 'penalize' ;
    options.UseParallel = 'never' ;
elseif isstruct(fitnessfcn)
    nvars = fitnessfcn.nvars ;
    Aineq = fitnessfcn.Aineq ;
    bineq = fitnessfcn.bineq ;
    Aeq = fitnessfcn.Aeq ;
    beq = fitnessfcn.beq ;
    LB = fitnessfcn.LB ;
    UB = fitnessfcn.UB ;
    nonlcon = fitnessfcn.nonlcon ;
    if ischar(nonlcon) && ~isempty(nonlcon)
        nonlcon = str2func(nonlcon) ;
    end
    options = fitnessfcn.options ;
    fitnessfcn = fitnessfcn.fitnessfcn ;
elseif nargin < 2
    msg = 'PSO requires at least two input arguments' ;
    error('%s, or a problem structure. Type >> help pso for details',...
        msg)
end % if ~nargin

if ~exist('options','var') % Set default options
    options = struct ;
end % if ~exist

options = psooptimset(options) ;

options.Verbosity = 1 ; % For options.Display == 'final' (default)
if strcmpi(options.Display,'off')
    options.Verbosity = 0 ;
elseif strncmpi(options.Display,'iter',4)
    options.Verbosity = 2 ;
elseif strncmpi(options.Display,'diag',4)
    options.Verbosity = 3 ;
end

if ~exist('Aineq','var'), Aineq = [] ; end
if ~exist('bineq','var'), bineq = [] ; end
if ~exist('Aeq','var'), Aeq = [] ; end
if ~exist('beq','var'), beq = [] ; end
if ~exist('LB','var'), LB = [] ; end
if ~exist('UB','var'), UB = [] ; end
if ~exist('nonlcon','var'), nonlcon = [] ; end

% Check for swarm stability
% -------------------------------------------------------------------------
if options.SocialAttraction + options.CognitiveAttraction >= 4 && ...
        options.Verbosity > 2
    msg = 'Warning: Swarm is unstable and may not converge ' ;
    msg = [msg 'since the sum of the cognitive and social attraction'] ;
    msg = [msg ' parameters is greater than or equal to 4.'] ;
    msg = [msg ' Suggest adjusting options.CognitiveAttraction and/or'] ;
    sprintf('%s options.SocialAttraction.',msg)
end
% -------------------------------------------------------------------------

% Check for constraints and bit string population type
% -------------------------------------------------------------------------
if strncmpi(options.PopulationType,'bitstring',2) && ...
        (~isempty([Aineq,bineq]) || ~isempty([Aeq,beq]) || ...
        ~isempty(nonlcon) || ~isempty([LB,UB]))
    Aineq = [] ; bineq = [] ; Aeq = [] ; beq = [] ; nonlcon = [] ;
    LB = [] ; UB = [] ;
    if options.Verbosity > 2
        msg = sprintf('Constraints will be ignored') ;
        msg = sprintf('%s for options.PopulationType ''bitstring''',msg) ;
        warning('%s',msg) ;
    end
end
% -------------------------------------------------------------------------

% Change this when nonlcon gets fully implemented:
% -------------------------------------------------------------------------
if ~isempty(nonlcon) && strcmpi(options.ConstrBoundary,'reflect')
    if options.Verbosity > 2
        msg = 'Non-linear constraints don''t have ''reflect'' boundaries' ;
        msg = [msg, ' implemented.'] ;
        warning('pso:main:nonlcon',...
            '%s Changing options.ConstrBoundary to ''penalize''.',...
            msg)
    end
    options.ConstrBoundary = 'penalize' ;
end
% -------------------------------------------------------------------------

% Is options.PopInitRange reconcilable with LB and UB constraints?
% -------------------------------------------------------------------------
% Resize PopInitRange in case it was given as one range for all dimensions
if size(options.PopInitRange,1) ~= 2 && size(options.PopInitRange,2) == 2
    % Transpose PopInitRange if user provides nvars x 2 matrix instead
    options.PopInitRange = options.PopInitRange' ;
elseif size(options.PopInitRange,2) == 1 && nvars > 1
    % Resize PopInitRange in case it was given as one range for all dim
    options.PopInitRange = repmat(options.PopInitRange,1,nvars) ;
elseif size(options.PopInitRange,2) ~= nvars
    msg = 'Number of dimensions of options.PopInitRange does not' ;
    msg = sprintf('%s match nvars. PopInitRange should be a',msg) ;
    error('%s  2 x 1 or 2 x nvars matrix.',msg) ;
end

% Check initial population with respect to bound constraints
% Is this really desirable? Maybe there are some situations where the user
% specifically does not want a uniform inital population covering all of
% LB and UB?
if ~isempty(LB) || ~isempty(UB)
    options.LinearConstr.type = 'boundconstraints' ;
    if isempty(LB), LB = -inf*ones(1,nvars) ; end
    if isempty(UB), UB =  inf*ones(1,nvars) ; end
    LB = reshape(LB,1,[]) ;
    UB = reshape(UB,1,[]) ;
    options.PopInitRange = ...
        psocheckpopulationinitrange(options.PopInitRange,LB,UB) ;
end
% -------------------------------------------------------------------------

% Check validity of VelocityLimit
% -------------------------------------------------------------------------
if all(~isfinite(options.VelocityLimit))
    options.VelocityLimit = [] ;
elseif isscalar(options.VelocityLimit)
    options.VelocityLimit = repmat(options.VelocityLimit,1,nvars) ;
elseif ~isempty(length(options.VelocityLimit)) && ...
        ~isequal(length(options.VelocityLimit),nvars)
    msg = 'options.VelocityLimit must be either a positive scalar' ;
    error('%s, or a vector of size 1xnvars.',msg)
end % if isscalar
options.VelocityLimit = abs(options.VelocityLimit) ;
% -------------------------------------------------------------------------

% Setup for parallel computing
% -------------------------------------------------------------------------
if strcmpi(options.UseParallel,'always')
    if strcmpi(options.Vectorized,'on')
        if options.Verbosity > 2 
            msg = 'Both ''Vectorized'' and ''UseParallel'' options have ' ;
            msg = [msg 'been set. The problem will be computed locally '] ;
            warning('%s using the ''Vectorized'' computation method.',...
                msg) ;
        end
    elseif isempty(ver('distcomp')) % Check for toolbox installed
        if options.Verbosity > 2 
            msg = 'Parallel computing toolbox not installed. Problem' ;
            warning('%s will be computed locally instead.',msg) ;
        end
        options.UseParallel = 'never' ;
    else
        poolalreadyopen = false ;
        if isempty(gcp('nocreate'))
            poolobj = parpool ;
            addAttachedFiles(poolobj,which(func2str(fitnessfcn))) ;
        else
            poolalreadyopen = true ;
        end
    end
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
  
209
  
210
  
211
  
212
  
213
  
214
  
215
  
216
  
217
  
218
  
219
  
220
  
221
  
222
  
223
  
224
  
225
  
226
  
227
  
228
  
229
  
230
  
231
  
232
  
233
  
234
  
235
  
236
  
237
  
238
  
239
  
240
  
241
  
242
  
243
  
244
  
245
  
246
  
247
  
248
  
249
  
250
  
251
  
252
  
253
  
254
  
255
  
256
  
257
  
258
  
259
  
260
  
261
  
262
  
263
  
264
  
265
  
266
  
267
  
268
  
269
  
270
  
271
  
272
  
273
  
274
  
275
  
276
  
277
  
278
  
279
  
280
  
281
  
282
  
283
  
284
  
285
  
286
  
287
  
288
  
289
  
290
  
291
  
292
  
293
  
294
  
295
  
296
  
297
  
298
  
299
  
300
  
301
  
302
  
303
  
304
  
305
  
306
  
307
  
308
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/114643681