【单目标优化求解】基于matlab海洋捕食者算法(MPA)求解单目标问题【含Matlab源码 478期】
一、获取代码方式
获取代码方式1:
通过订阅紫极神光博客付费专栏,凭支付凭证,私信博主,可获得此代码。
获取代码方式2:
完整代码已上传我的资源:【单目标优化求解】基于matlab海洋捕食者算法(MPA)求解单目标问题【含Matlab源码 478期】
备注:订阅紫极神光博客付费专栏,可免费获得1份代码(有效期为订阅日起,三天内有效);
二、海洋捕食者算法(MPA)简介
1 海洋捕食者算法(MPA)定义
海洋捕食者算法(MPA)是一种自然启发式的优化算法,它遵循在最佳觅食策略中自然支配的规则,并且在海洋生态系统中遇到捕食者与猎物之间的速率策略。
2 海洋捕食者算法(MPA)流程
(1) 初始化精英矩阵(Elite)和猎物矩阵(Prey)
猎物矩阵(Prey) 矩阵每一个元素 Xij 的初始化方法:
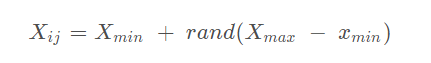
最终得到的Prey矩阵:

其中,n是种群的规模,d是每个维度的位置(问题的解的维度)。
对每一个Prey个体Xi = [Xi,1, Xi,2, …, Xi,d], 计算其适应度, 然后使用适应度最优的个体 XI 复制n份构成Elite矩阵

其中n是种群的规模,d是每个维度的位置(问题的解的维度),Elite的维度与Prey的维度相同。
(2)接着我们开始进行优化。在优化的过程中,具有三个步骤。
步骤一:
当迭代次数小于最大迭代次数的三分之一的时候
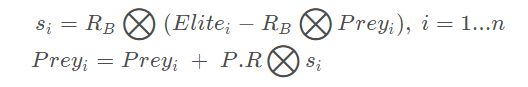
其中,RB 是采用布朗随机游走产生的随机数组成的向量,维度是 d(问题的求解规模,下同)。si 代表移动的步长。 P是一个常数,等于0.5。R是一个0到1之间的均匀分布的随机数组成的向量,维度是 d。
RB相当于一般化的高斯分布(Normal Gaussian distribution)。每一个元素 RBi 可以通过下列表达式来计算:
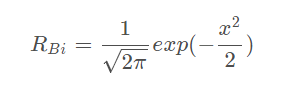
步骤二:
当迭代次数大于最大迭代次数的三分之一而小于其三分之二时,种群分两部分进行操作。
前半部分种群跟新规则如下:
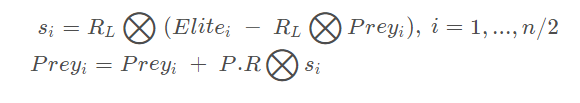
其中, RL 是 Levy 分布组成的出来的一个向量,维度是 d。P是一个常数,等于0.5。R是一个0到1之间的均匀分布的随机数组成的向量,维度是 d。
RL 的每一项元素 RLi 可以由下列式子计算得来:
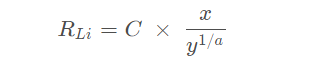
其中,C 和 α是一个常数,分别等于0.05和1.5。
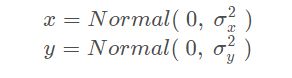
在上面的表达式中
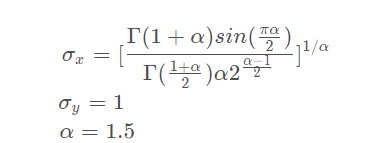
后半部分种群跟新规则如下:
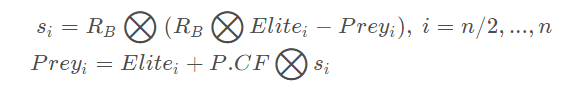
这里RB 是采用布朗随机游走产生的随机数组成的向量,维度是 d。P是常数,等于0.5。CF是步长si 的自适应参数(下同), 定义为
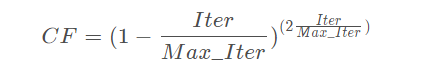
其中, Iter是迭代次数,Max_Iter是最大迭代次数。
步骤三:
当迭代次数大于最大迭代次数的三分之二时,进入第三个阶段,此时种群更新规则如下:
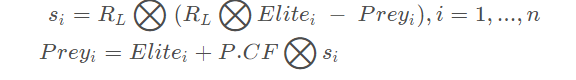
(3) 解决涡流形成和FADS效应(Eddy formation and FADs’ effect)
此操作的作用是让算法在迭代过程中尽可能跳出局部最优解,已达到更好的寻优精度。
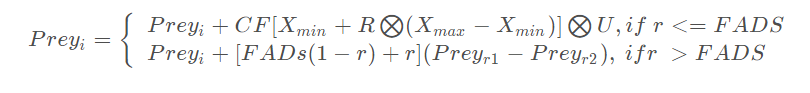
其中r是一个随机数, FADS是一个影响优化过程的常数,等于0.2。r1和r2是Prey两个随机下标, 1 ≤ r1,r2 ≤ n。 U是一个包含0和1的二进制向量,维度是d。U的每一个元素 Ui 定义为
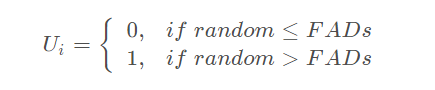
其中random是一个0到1的随机数,FADs等于0.2。
(4) 海洋记忆(Marine memory)
这一步骤进行对Elite(精英)矩阵的更新。
针对每一个Prey矩阵中的个体Preyi ,计算其适应度,若适应度由于Elite矩阵矩阵中相应的位置的适应度时,则将该个体替代原来精英矩阵中相应的个体。然后在计算整个精英矩阵中最优个体的适应度,若符合要求,则算法结束,否则继续迭代。
算法的流程图总结出来如下:

三、部分源代码
%_________________________________________________________________________
% Marine Predators Algorithm source code (Developed in MATLAB R2015a)
%
% programming: Afshin Faramarzi & Seyedali Mirjalili
%
% paper:
% A. Faramarzi, M. Heidarinejad, S. Mirjalili, A.H. Gandomi,
% Marine Predators Algorithm: A Nature-inspired Metaheuristic
% Expert Systems with Applications
% DOI: doi.org/10.1016/j.eswa.2020.113377
%
% E-mails: afaramar@hawk.iit.edu (Afshin Faramarzi)
% muh182@iit.edu (Mohammad Heidarinejad)
% ali.mirjalili@laureate.edu.au (Seyedali Mirjalili)
% gandomi@uts.edu.au (Amir H Gandomi)
%_________________________________________________________________________
% --------------------------------------------
% fobj = @YourCostFunction
% dim = number of your variables
% Max_iteration = maximum number of iterations
% SearchAgents_no = number of search agents
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n
% ---------------------------------------------------------
clear all
clc
format long
SearchAgents_no=25; % Number of search agents
Function_name='F23';
Max_iteration=500; % Maximum number of iterations
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,Convergence_curve]=MPA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
% function topology
figure('Position',[500 400 700 290])
subplot(1,2,1);
func_plot(Function_name);
title('Function Topology')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
% Convergence curve
subplot(1,2,2);
semilogy(Convergence_curve,'Color','r')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
%_________________________________________________________________________
% Marine Predators Algorithm source code (Developed in MATLAB R2015a)
%
% programming: Afshin Faramarzi & Seyedali Mirjalili
%
% paper:
% A. Faramarzi, M. Heidarinejad, S. Mirjalili, A.H. Gandomi,
% Marine Predators Algorithm: A Nature-inspired Metaheuristic
% Expert Systems with Applications
% DOI: doi.org/10.1016/j.eswa.2020.113377
%
% E-mails: afaramar@hawk.iit.edu (Afshin Faramarzi)
% muh182@iit.edu (Mohammad Heidarinejad)
% ali.mirjalili@laureate.edu.au (Seyedali Mirjalili)
% gandomi@uts.edu.au (Amir H Gandomi)
%_________________________________________________________________________
% This function containts full information and implementations of the benchmark
% functions in Table 1, Table 2, and Table 3 in the paper
% lb is the lower bound: lb=[lb_1,lb_2,...,lb_d]
% up is the uppper bound: ub=[ub_1,ub_2,...,ub_d]
% dim is the number of variables (dimension of the problem)
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=50;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=50;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=50;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=50;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=50;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=50;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=50;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=50;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=50;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=50;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=50;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=50;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=50;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
四、运行结果

五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/114573304
- 点赞
- 收藏
- 关注作者


评论(0)