【BP数据预测】基于matlab人工鱼群算法优化BP神经网络数据预测【含Matlab源码 523期】
一、人工鱼群算法简介
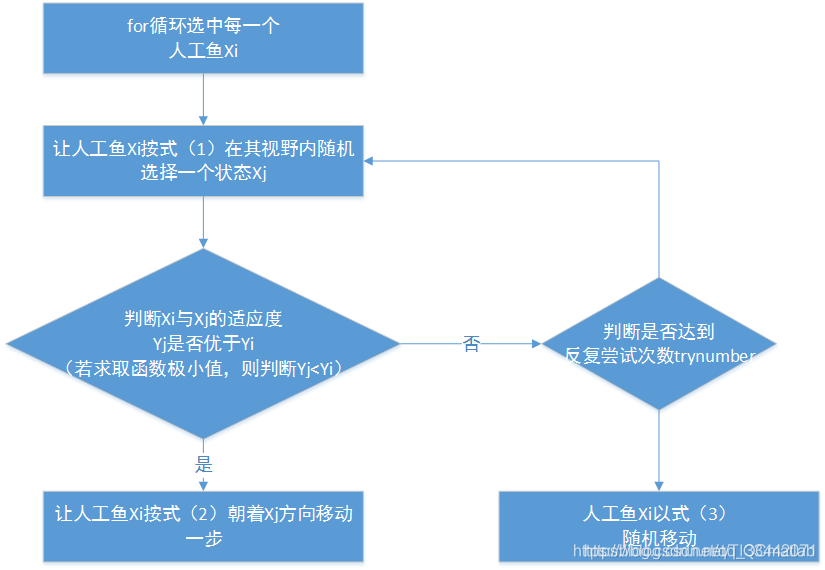
1 觅食行为
指鱼循着食物多的方向游动的一种行为,人工鱼X i X_iXi在其视野内随机选择一个状态X j X_jXj,分别计算它们的目标函数值进行比较,如果发现Y j Y_jYj比Y i Y_iYi优(Y j Y_jYj和Y i Y_iYi分别为X j X_jXj和X i X_iXi的适应度值),则Xi向Xj的方向移动一步;否则,X i X_iXi继续在其视野内选择状态X j X_jXj,判断是否满足前进条件,反复尝试t r y n u m b e r trynumbertrynumber次后,仍没有满足前进条件,则随机移动一步使X i X_iXi到达一个新的状态。表达式如下:
X j = X i + r a n d ( ) ∗ v i s u a l (1) X_j=X_i+rand()*visual \tag{1}Xj=Xi+rand()∗visual(1)
X n e x t = X i + r a n d ( ) ∗ s t e p ∗ X j − X i ∣ ∣ X j − X i ∣ ∣ (2) X_{next}=X_i+rand()step\frac{X_j-X_i}{\left | \left | X_j-X_i \right | \right |}\tag{2}Xnext=Xi+rand()∗step∗∣∣Xj−Xi∣∣Xj−Xi(2)
X n e x t = X i + r a n d ( ) ∗ s t e p (3) X_{next}=X_i+rand()*step \tag{3}Xnext=Xi+rand()∗step(3)
其中rand()是介于0和1之间的随机数。
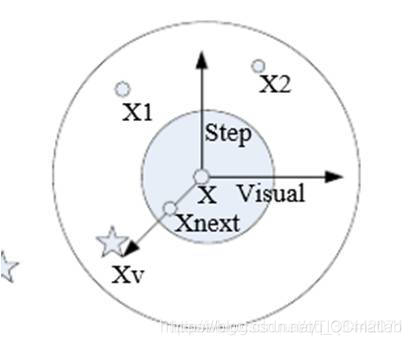
人 工 鱼 的 视 觉 描 述 人工鱼的视觉描述人工鱼的视觉描述
框架图如下所示:
伪代码段如下:
for i = 1:N
for j = 1:Try_number
Xj=x(i)+Visual.*rand();%人工鱼Xi按式(1)在其视野内随机选择一个状态Xj
if f(Xj)<f(x(i)) %比较Xj和Xi的适应度
X_next= x(i)+rand()*step*(Xj-x(i))/norm(Xj-x(i)); %人工鱼Xi按式(2)朝着Xj方向移动一步,norm()函数表示二范数
break;
else
X_next=x(i)+step*rand();
end
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
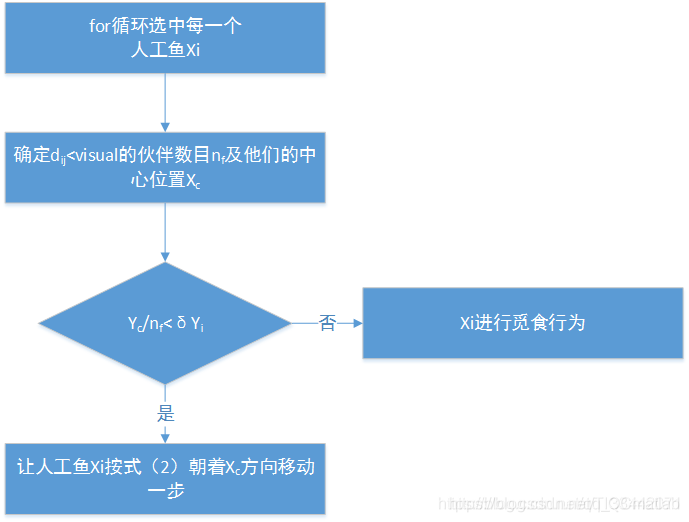
2 聚群行为
鱼在游动过程中为了保证自身的生存和躲避危害会自然地聚集成群 。人工鱼X i X_iXi搜索其视野内(d i j < v i s u a l d_{ij}<visualdij<visual)的伙伴数目n f n_fnf及中心位置X c X_cXc,若Y c / n f < δ Y i Y_c/n_f< δY_iYc/nf<δYi(求极小值时使用小于号,在求极大值时则相反;Y c Y_cYc和Y i Y_iYi分别为X c X_cXc和X i X_iXi的适应度值),表明伙伴中心位置状态较优且不太拥挤,则X i X_iXi朝伙伴的中心位置移动一步,否则执行觅食行为;
框架图如下所示:
伪代码段如下:
nf=0;X_inside=0;
for i = 1:N
for j = 1:N
if norm(x(j)-x(i))<Visual % 求人工鱼Xi与其他人工鱼之间的距离
nf = nf+1; %统计在视野范围内的鱼数量
X_inside= X_inside+x(j); %将视野范围内的鱼进行累加
end
X_inside=X_inside-x(i); %需要去除Xi本身;因为在 一开始计算时,i=j,把中心的鱼也进行了一次计算
nf=nf-1;
Xc = X_inside/nf; %此时Xc表示Xi感知范围其他伙伴的中心位置;
if f(Xc)/nf < δ*f(x(i))
x_next=x(i)+rand*Step*(Xc-x(i))/norm(Xc-x(i));
else
进行觅食行动
end
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
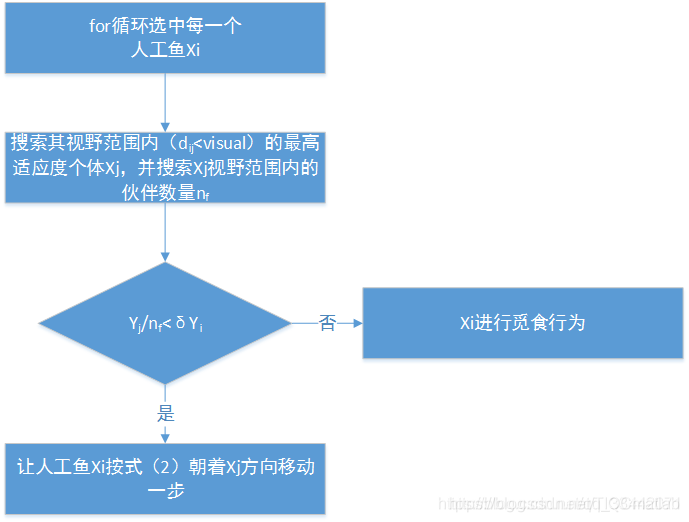
3 追尾行为
指鱼向其视野区域内的最优方向移动的一种行为。人工鱼X i X_iXi搜索其视野内(d i j < v i s u a l d_{ij}<visualdij<visual)适应度最高的个体X j X_jXj,其适应度值为Y j Y_jYj,并探索人工鱼X j X_jXj视野内的伙伴数目n f n_fnf,若Y j / n f < δ Y i Y_j/n_f< δY_iYj/nf<δYi,表明X j X_jXj状态较优且不太拥挤,则X i X_iXi朝X j X_jXj位置移动一步,否则执行觅食行为;
框架图如下所示:
伪代码段如下:
Y_max=inf;nf=0;
for i = 1:N
%搜索人工鱼Xi视野范围内的最高适应度个体Xj
for j = 1:N
if norm(x(j)-x(i))<Visual && f(x(j))<Y_max % 求人工鱼Xi与其他人工鱼之间的距离
X_max=x(j);
Y_max=f(x(j));
end
end
%搜索人工鱼Xj视野范围内的伙伴数量
for j = 1:N
if(norm(x(j)-X_max)<Visual)
nf=nf+1;
end
end
nf=nf-1;%去掉他本身
if Y_max/nf<delta*f(x(i))
x_next= x(i,:)+rand*Step.*(temp_maxX-x(i,:))./norm(temp_maxX-x(i,:));
else
进行觅食行为;
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
4 算法总述
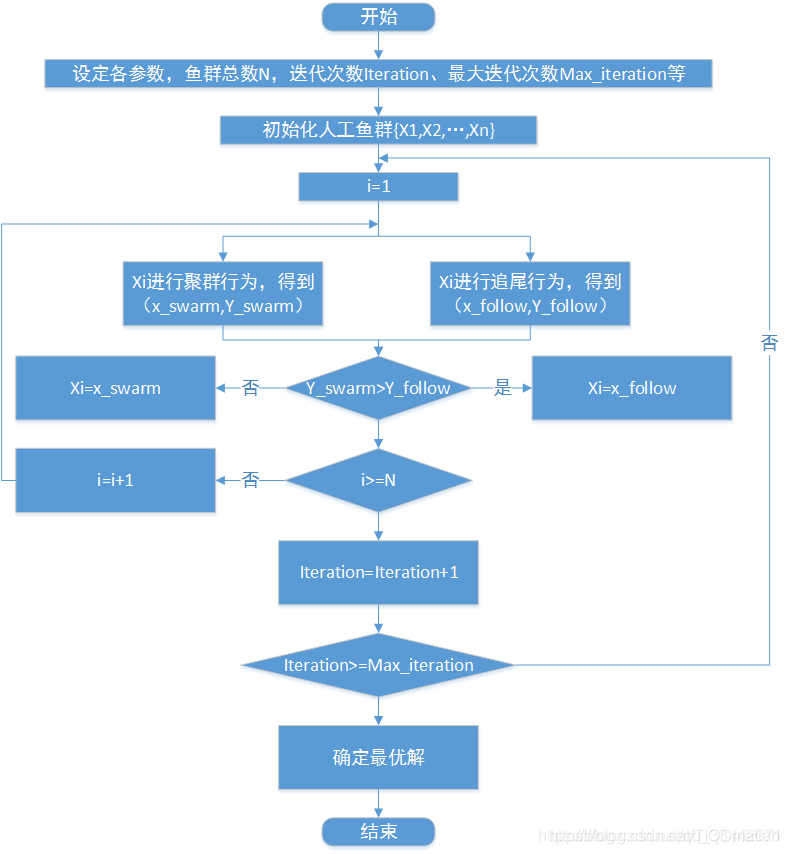
综上所述,算法在运算过程中,会同时进行聚群和追尾行为。而觅食行为属于这两种行为中发现聚群对象或者追尾对象附近拥挤度过大时,人工鱼选择的行为方式,若在觅食过程中,未发现比自身适应度高的人工鱼,则按步长step随机移动。最后对聚群行为和追尾行为得到的适应度值进行比较,选择优秀的人工鱼作为下一代的个体。其总框架图如下:
2 分析拥挤度因子δ δδ
2.1 拥挤度因子的取值
在求极小值问题中:δ = α n m a x , α ∈ ( 0 , 1 ] δ=αn_{max}, α∈(0,1]δ=αnmax,α∈(0,1]
在求极大值问题中:δ = 1 α n m a x , α ∈ ( 0 , 1 ] δ=\frac{1}{αn_{max}},α∈(0,1]δ=αnmax1,α∈(0,1]
其中α αα为极值接近水平,n m a x n_{max}nmax为期望在该邻域内聚集的最大人工鱼数目。
2.2 拥挤度因子的作用机理
对追尾行为的描述
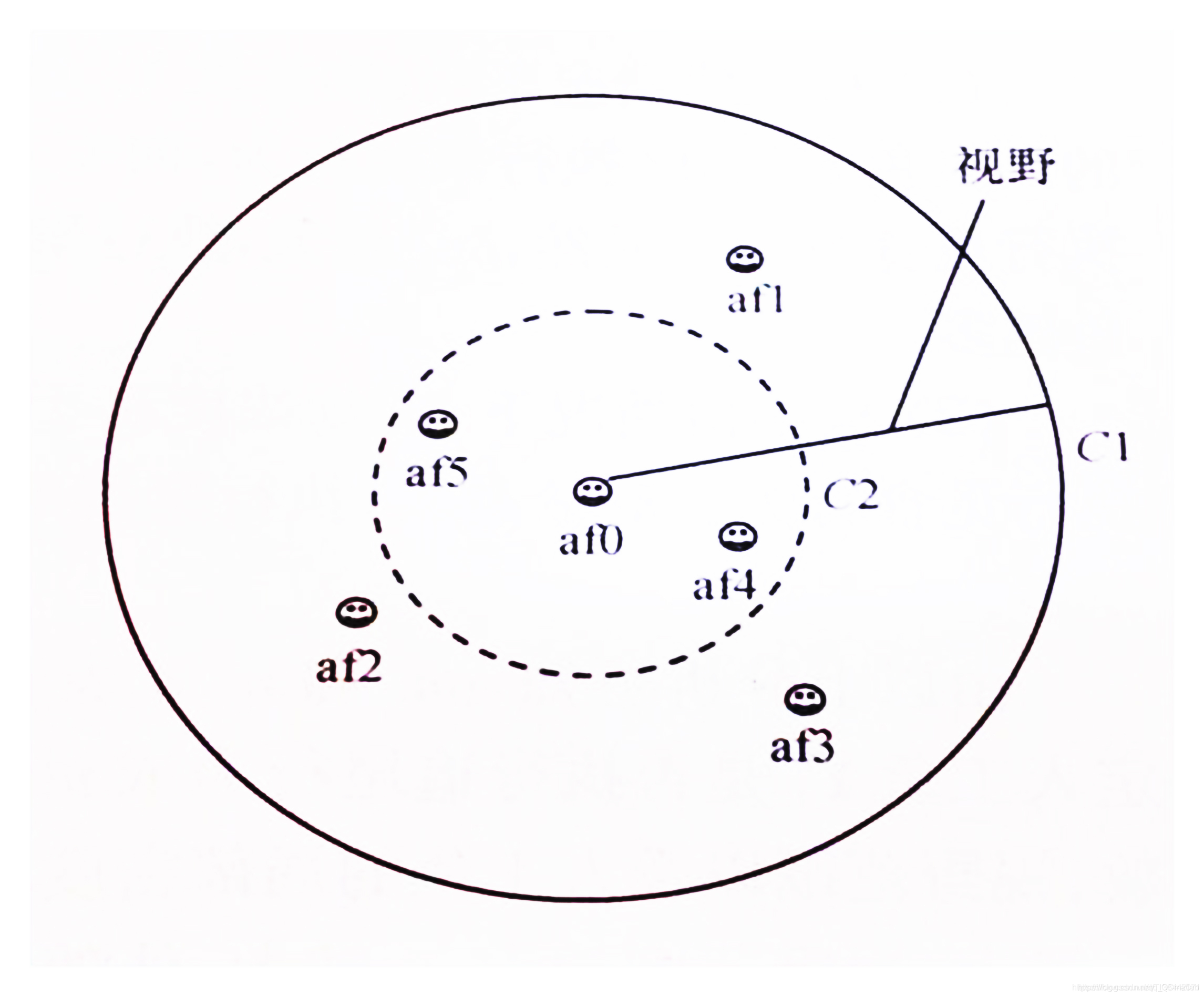
图中af0为人工鱼af1-5在各自视野内的最优人工鱼,其实物浓度为Y j Y_jYj,C1为以af0为圆心,以视野范围为半径的圆,即能探知af0的最远距离,人工鱼越靠近af0,状态越优。
求极大值情况下:当δ n f ≤ 1 δn_f\leq 1δnf≤1时,所有人工鱼af1-5都执行追尾行为,向af0游动;
δ = 1 α n m a x δ=\frac{1}{αn_{max}}δ=αnmax1
δ n f = n f α n m a x ≤ 1 δn_f =\frac{n_f}{αn_{max}}\leq 1δnf=αnmaxnf≤1
当α αα=1的时候,可以明显看出来n f ≤ n m a x n_f \leq n_{max}nf≤nmax,即说明人工鱼视野范围内不拥挤。
当δ n f > 1 δn_f >1δnf>1时,若C2的食物浓度为Y j δ n f \frac{Y_j}{δn_f }δnfYj的等浓度食物圈,则C2与C1间的人工鱼af1、af2、af3执行追尾行动,向af0游动,人工鱼af4、af5执行觅食行为。此时δnf 越大执行追尾行动的人工鱼越少,反之越多。
2.3 拥挤度因子的影响
以极大值为例(极小值的情况正好和极大值相反), δ δδ越大,表明允许的拥挤程度越小,人工鱼摆脱局部最优的能力越强;但是收敛的速度会有所减缓,这主要因为人工鱼在逼近极值的同时,会因避免过分拥挤而随机走开或者受其它人工鱼的排斥作用,不能精确逼近极值点。可见,δ δδ的引入避免了人工鱼过度拥挤而陷入局部极值,另一方面,该参数会使得位于极值点附近的人工鱼之间存在相互排斥的影响,而难以向极值点精确逼近,所以,对于某些局部极值不是很严重的具体问题,可以忽略拥挤的因素,从而在简化算法的同时也加快了算法的收敛速度和提高结果的精确程度。
二、部分源代码
%%%%%%%%%%%%人工鱼算法优化BP神经网络%%%%%%%%%%%%%%%%%%%%%%%%%
tic; %计时开始
clc; %清屏
clear all; %清除所有变量
close all;
%% 载入数据
load gqpin.txt;
load gqpout.txt;
p=gqpin;
t=gqpout;
%训练集141个
input_train=p(1:end,:);
output_train=t(1:end,:);
% 输入输出数据归一化
[inputn,inputps]=mapminmax(input_train');
[outputn,outputps]=mapminmax(output_train');
inputn=inputn';
outputn=outputn';
x1=inputn(:,1);
y1=outputn;
x2=inputn(:,2);
y2=outputn;
x3=inputn(:,3);
y3=outputn;
x4=inputn(:,4);
y4=outputn;
x5=inputn(:,5);
y5=outputn;
XX1=[x1,x2,x3,x4,x5];
YY1=[y1,y2,y3,y4,y5];
DATA=[XX1 YY1];
m=DATA(randint(1,100,[1,length(DATA)]),:); %随机抽取100个数据样本
X_sample=m(:,1:5); %X(261,5)
Y_sample=m(:,6:10); %Yo(261,5)
input=size(X_sample,1); %输入层神经元个数
middle=100; %显示中间层神经元个数
output=size(X_sample,1); %显示输出层神经元个数
%%%%
v=rands(input,middle); %初始化连接权矩阵v(i,j) :输入层与中间层的连接权
w=rands(middle,output); %初始化连接权矩阵w(j,t) :中间层与输出层的连接权
th1=rands(middle,1); %初始化中间层阈值矩阵th1 :中间层的阈值
th2=rands(output,1); %初始化输出层阈值矩阵th2 :输出层的阈值
out_middle=zeros(middle,1); %中间层的实际输出
out_output=zeros(output,1); %输出层的实际输出
delta_output=zeros(output,1); %输出层的差值
delta_middle=zeros(middle,1); %中间层的差值
sample_bumbers=5; %样本数
max_times=10; %最大训练次数
times=0; %训练次数
eta=0.1; %学习系数eta
gamma=0.1; %学习系数gamma
alpha=0.3; %动量系数
sample_pointer=0; %样本数指针
error_max=0.01; %最大误差
error_global=1; %全局误差
%%%%%%人工鱼算法初始化%%%%%%%%%%%
fishnum=50; %生成50条人工鱼
MAXGEN=10; %最大迭代次数
try_number=50; %最大试探次数
visual=1; %感知距离
delta=0.618; %拥挤度因子
step=0.01; %移动步长
for times=1:max_times %begin for External Loop
if error_global>error_max %begin for if
error_global=0; %全局误差
for sample_pointer=1:sample_bumbers
X0=X_sample(:,sample_pointer); %分别输入模式x1,x2,x3:(16,1) >>>X(16,36),X0(16,1)
Y0=Y_sample(:,sample_pointer); %分别输入模式y1,y2,y3:(3,1) >>>Yo(3,3),Y0(3,1)
%计算中间层的输出:
Y=v'*X0-th1; %Y(8,1)=v'(8,16)*X0(16,1)*-th1(8,1),计算中间层的输入
for j=1:middle
out_middle(j)=1/(1+exp(-Y(j))); %out_middle(1,8):中间层输出
end
%计算输出层输出:
Y=w'*out_middle-th2; %Y(3,1)=w'(3,8)*out_middle(8,1)*-th2(3,1),计算输出层的输入
output_error(sample_pointer)=0;
for k=1:output
%%%初始化鱼群
lb_ub=[-1,2,1];
X=AF_init(fishnum,lb_ub);
LBUB=[];
for i=1:size(lb_ub,1)
LBUB=[LBUB;repmat(lb_ub(i,1:2),lb_ub(i,3),1)];
end
gen=1;
BestY=-1*ones(1,MAXGEN);
BestX=-1*ones(1,MAXGEN);
besty=-100;
Y=AF_foodconsistence(X);
if gen<=MAXGEN
for i=1:fishnum
[Xi1,Yi1]=AF_swarm(X,i,visual,step,delta,try_number,LBUB,Y);%聚群行为;
[Xi2,Yi2]=AF_follow(X,i,visual,step,delta,try_number,LBUB,Y);%追尾行为;
if Yi1>Yi2
X(:,i)=Xi1;
Y(1,i)=Yi1;
else
X(:,i)=Xi2;
Y(1,i)=Yi2;
end
end
[Ymax,index]=max(Y);
if Ymax>besty
besty=Ymax;
bestx=X(:,index);
BestY(gen)=Ymax;
[BestX(:,gen)]=X(:,index);
else
BestY(gen)=BestY(gen-1);
[BestX(:,gen)]=BestX(:,gen-1);
end
gen=gen+1;
else
break;
end
out_output(k)=Y0(k)-bestx;
error=(Y0(k)-out_output(k))*(Y0(k)-out_output(k))/2; %error为应有输出和实际输出之间的差值
output_error(sample_pointer)=output_error(sample_pointer)+error;
end
%计算所有样本的总体误差error_global
error_global=error_global+output_error(sample_pointer);
error_global=error_global/3;
%计算输出层校正误差delta_output:
for k=1:output
delta_output(k)=(Y0(k)-out_output(k))*out_output(k)*(1-out_output(k));
%delta_output(k)=delta_o(k)
end
%计算中间层校正误差delta_middle:
for j=1:middle
beta(j)=delta_output'*w(j,:)';
delta_middle(j)=beta(j)*out_middle(j)*(1-out_middle(j));
end
%计算下一次的中间层和输出层之间的连接权w(i,j),阈值th2(j)
pre_w=0;pre_th2=0;
for k=1:output;
for j=1:middle
w(j,k)=w(j,k)+eta*delta_output(k)*out_middle(j)+alpha*pre_w; %out_middle(j)=y(j)
pre_w=eta*delta_output(k)*out_middle(j);
end
th2(k)=th2(k)+eta*delta_output(k)+alpha*pre_th2;
pre_th2=eta*delta_output(k);
end
v(i,j)=v(i,j)+gamma*X0(i)*delta_middle(j)+alpha*pre_v; %调节输入层和中间层之间的连接权w(i,j)
pre_v=gamma*X0(i)*delta_middle(j);
end
th1(j)=th1(j)+gamma*delta_middle(j)+alpha*pre_th1; %调节中间层的阈值th1(j,1)
pre_th1=gamma*delta_middle(j);
end
end %end for "for sample_pointer=1:sample_bumbers"
else
break; %当output_error<error_max时,结束调节过程
end %end for else
end %end for "for times=1:max_times"
%预测结果反归一化
Y1=mapminmax('reverse',Y0,outputps);
out_output1=mapminmax('reverse',out_output,outputps);
disp('^^^^^^^^^^^^^显示结果:^^^^^^^^^^^^^^');
fprintf('总训练次数为:%d.\n',times);
fprintf('运行时间为:\n');
toc; %计时结束,并输出程序的运行时间
error2=Y1-out_output1;
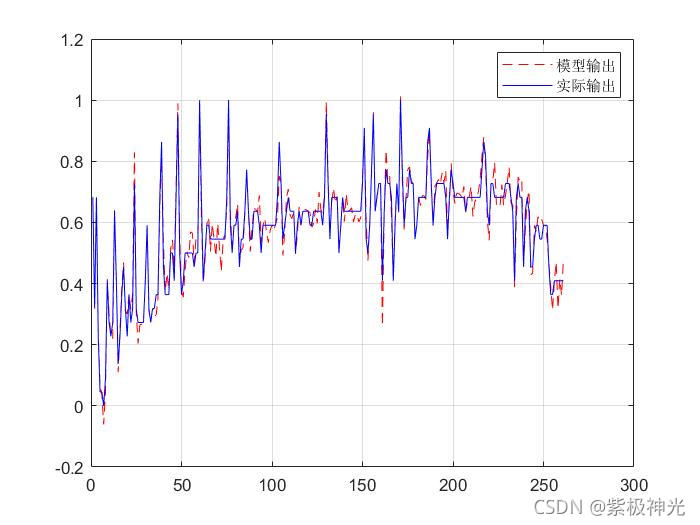
figure(1)
plot(out_output1,'r--');
hold on
plot(Y1,'b');
legend('模型输出','实际输出');
figure(2)
plot(Y1-out_output1,'-');
xlabel('输入样本'),ylabel('样本输出误差'),title('E误差');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
三、运行结果
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/114853881
- 点赞
- 收藏
- 关注作者


评论(0)