【图像融合】基于matlab PCA图像融合【含Matlab源码 723期】
一、获取代码方式
获取代码方式1:
通过订阅紫极神光博客付费专栏,凭支付凭证,私信博主,可获得此代码。
获取代码方式2:
完整代码已上传我的资源:【图像融合】基于matlab PCA图像融合【含Matlab源码 723期】
备注:
订阅紫极神光博客付费专栏,可免费获得1份代码(有效期为订阅日起,三天内有效);
二、图像融合与PCA算法简介
1 图像融合概念与分类
图像融合是将针对同一场景不同来源的图像通过特定的算法生成一张新的图像,融合后的图像综合
了不同源图像间的互补信息,提高了后期图像可被分析和加工处理的能力。图像融合主要分为像素级融合、特征级融合以及决策级融合。
像素级融合直接处理原始像素点,要求不同源生成的图像匹配度高,因此图像保留的信息量大,但是
运算量巨大:特征级融合需要先提取各源图像的特征信息,然后利用加权的特征信息进行图像重建,该融合方式容易丢失图像的部分信息:决策级融合是综合运用像素级融合与特征级融合,通过对图像的分析依据具体情况找到最优匹配。图像融合分类示意见图。
融合后的图像一般需要进行质量评估,主观方法就是人眼判断融合图像的质量好坏。客观方法包含与
源图像进行相关指标的计算、比对,例如均值、标准差、平均梯度、信息熵、空间频率等.
2 PCA算法原理
主成分分析技术PC A(principal components analysis) , 也叫做主分量分析, 基本数学原理是K-L正交分解。K-L变换是通过原始信号集合构造正交基,信号与基进行积分运算后,每个基对应的系数表示原始信号在该基下的投影值。在连续信号领域,可通过信号的内在特征构造核函数,不同的变换核函数
对应不同的基:在离散领域,变换核函数变为变换矩阵,当变换矩阵为协方差矩阵时,离散K-L变换即为PCA。
设原始信号在本征空间, PC A可以理解为一种信号降维算法,通过协方差矩阵构造出一组基,使得
赋范子空间基信号的加权之和与本征空间误差最小,即投影误差最小。PC A变换后的每个基的系数即为本征空间在子空间下的投影值,此时可以选取有限个基的不同组合向原始信号通近I],对于非稀疏矩阵,理论上只需少量包含信息量大的基投影,即可在相当程度上近似于本征空间。设离散随机信号为X,X为n行p列矩阵,见式(1)。

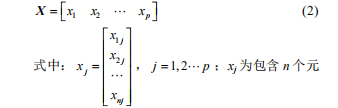
现以列为投影方向构造子空间的基(以行为方向同理),X可改写为式(2)。
j=1,2…p:x为包含n个元素的列向量。
设变换矩阵为A,X变换后的矩阵为F,则F见式(3)。

当按列方向投影时, 需保证n多p, 此时A为pxp方阵:同理, 当按行方向投影时需保证n≤p, A为nxn
方阵,A就是要构造的基回。此时式(3)可写为式(4)。

1.3 变换矩阵的计算
通过1.2节的原理分析,只要构造出满足3个条件的变换矩阵A,就可以对信号X进行主成分分析,得到主成分矩阵F,并利用F子列的任意组合得到重构信号X。在高等代数里,按列投影时,变换矩阵A就是信号X的协方差矩阵的特征向量按列组成的矩阵。同理,按行投影时,变换矩阵A就是信号X的协方差矩阵的特征向量按行组成的矩阵[1],证明略,只给出


2 图像的融合
对于灰度图像采用PCA算法时, 所得主成分矩阵的列与图像的列长度相等,重构图像会出现栅栏效
应, 原因是PC A算法是一种降维算法, 将二维图像降维成一维向量了,所以在对图像采用该算法时,一般采用多通道图像, 最简单的多通道图像就是RGB彩色图像。
图像融合基本原理:通过PC A正变换分别将2个待融合的三通道彩色图像,降维成3个单通道图像,即3个主成分,用另一幅图像的某个主成分替换掉该图像的某个主成分, 然后进行PC A逆变换, 得到的重构图像即为融合图像。
具体计算过程如下所述。
1)设可见光彩色图像为Xi,红外光伪彩色图像为X, 两图像的分辨率都为MXN, 通道数都为3, 分辨
率不同时可通过尺度缩放保持一致,通道数不同时可通过低通道数图像直接取代高通道数图像的主成分。
2)设X在3个通道下的图像分别为X1,Xi2,X 13, 即大小都是M×N的矩阵, 将其变为包含MXN个元素的列向量,记为X1,X12,X’13。
3)将X1,X12,X13组合成X。X=Xxi此时X为行数为MXN, 列数为3的矩阵, 依次带入式(7一11),得到转换矩阵A。
4)通过式(4)得到主成分矩阵F,此时的F是行数为MXN, 列数为3的矩阵, 提取第1列, 将其转化为MXN的矩阵, 则恰好对应X的第1主成分Fu,Fi就是图像Xi的第1主成分图像,第2主成分图像、第3主成分图像分别为F12,F13。同理,可以求出图像X的3个主成分图像为F21,F22,F23。
5)将Fi,Fz(ij=1,2,3)互换,并按式(6)作逆变换,即可求出融合图像Y,不同的互换组合可以求出不同的Y, Xu, X 2; (i=1.2.3) 不仅可以是RGB通道下的分解, 也可以是HIS空间、YUV空间下的分解[14],如此可以得到更多的Y。
三、部分源代码
% function Pca = PCA(TM);
clear
g_R=0; %r清晰度描述
g_G=0; %g清晰度描述
g_B=0; %b清晰度描述
h_R=0; %熵的描述
h_G=0;
h_B=0;
fenzi_R=0;
fenzi_G=0;
fenzi_B=0;
fenmu_up_R=0;
fenmu_up_G=0;
fenmu_up_B=0;
fenmu_low_R=0;
fenmu_low_G=0;
fenmu_low_B=0;
init_up_R=[];
init_up_G=[];
init_up_B=[];
init_low_R=[];
init_low_G=[];
init_low_B=[];
up=imread('high.jpg'); %读图像
low=imread('low.jpg');
figure(1)
imshow(up); %读RGB数值
title('PCA-RGB表示的高分辨率图像');
figure(2)
imshow(low);
title('PCA-RGB表示的低分辨率图像');
[up_R]=double(up(:,:,1));
[up_G]=double(up(:,:,2));
[up_B]=double(up(:,:,3));
[low_R]=double(low(:,:,1));
[low_G]=double(low(:,:,2));
[low_B]=double(low(:,:,3));
[M,N,color]=size(up);
up_Mx = 0;
low_Mx=0;
for i = 1 : M
for j = 1 : N
up_S = [up_R(i,j),up_G(i,j),up_B(i,j)]'; % 生成由R,G, B组成的三维列向量
up_Mx = up_Mx + up_S;
low_S = [low_R(i,j),low_G(i,j),low_B(i,j)]';
low_Mx = low_Mx + low_S;
end
end
up_Mx = up_Mx / (M*N); % 计算三维列向量的平均值
low_Mx = low_Mx / (M*N);
up_Cx = 0;
low_Cx=0;
for i = 1 : M
for j = 1 : N
up_S = [up_R(i,j),up_G(i,j),up_B(i,j)]';
up_Cx = up_Cx + up_S*up_S';
low_S = [low_R(i,j),low_G(i,j),low_B(i,j)]';
low_Cx = low_Cx + low_S*low_S';
end
end
up_Cx = up_Cx / (M * N)- up_Mx*up_Mx'; % 计算协方差矩陈
low_Cx = low_Cx / (M * N)- low_Mx*low_Mx';
[up_A,up_latent] = eigs(up_Cx); % 协方差矩陈的特征向量组成的矩陈----PCA变换的系数矩陈,特征值
[low_A,low_latent] = eigs(low_Cx);
for i = 1 : M
for j = 1 : N
up_X = [up_R(i,j),up_G(i,j),up_G(i,j)]'; % 生成由R,G, B组成的三维列
up_Y = up_A'*up_X; % 每个象素点进行PCA变换正变换
up_Y = up_Y';
up_R(i,j) = up_Y(1); % 高分辨率图片的第1主分量
up_G(i,j) = up_Y(2); % 高分辨率图片的第2主分量
up_B(i,j) = up_Y(3); % 高分辨率图片的第3主分量
low_X = [low_R(i,j),low_G(i,j),low_G(i,j)]';
low_Y = low_A'*low_X;
low_Y = low_Y';
low_R(i,j) = low_Y(1); % 低分辨率图片的第1主分量
low_G(i,j) = low_Y(2); % 低分辨率图片的第2主分量
low_B(i,j) = low_Y(3); % 低分辨率图片的第3主分量
end
end
for i = 1 : M
for j = 1 : N
up_Y = [up_R(i,j),up_G(i,j),up_B(i,j)]'; % 生成由R,G, B组成的三维列向量
up_X = up_A*up_Y; % 每个象素点进行PCA变换反变换
up_X = up_X';
up_r(i,j) = up_X(1);
up_g(i,j) = up_X(2);
up_b(i,j) = up_X(3);
low_Y = [up_R(i,j),low_G(i,j),low_B(i,j)]';
low_X = low_A*low_Y;
low_X = low_X';
low_r(i,j) = low_X(1);
low_g(i,j) = low_X(2);
low_b(i,j) = low_X(3);
end
end
%RGB(:,:,1)=up_r;
%RGB(:,:,2)=up_g;
%RGB(:,:,3)=up_b;
RGB(:,:,1)=low_r;
RGB(:,:,2)=low_g;
RGB(:,:,3)=low_b;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 下面是计算相关系数 %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
init_up_R=ones(M,N)*mean(up_R(:));
init_up_G=ones(M,N)*mean(up_G(:));
init_up_B=ones(M,N)*mean(up_B(:));
init_low_R=ones(M,N)*mean(low_R(:));
init_low_G=ones(M,N)*mean(low_G(:));
init_low_B=ones(M,N)*mean(low_B(:));
for i=1:M
for j=1:N
fenzi_R=fenzi_R+(up_R(i,j)-init_up_R(i,j))*(low_R(i,j)-init_low_R(i,j));
fenmu_up_R=fenmu_up_R+(up_R(i,j)-init_up_R(i,j))^2;
fenmu_low_R=fenmu_low_R+(low_R(i,j)-init_low_R(i,j))^2;
fenzi_G=fenzi_G+(up_R(i,j)-init_up_G(i,j))*(low_R(i,j)-init_low_G(i,j));
fenmu_up_G=fenmu_up_G+(up_R(i,j)-init_up_G(i,j))^2;
fenmu_low_G=fenmu_low_G+(low_R(i,j)-init_low_G(i,j))^2;
fenzi_B=fenzi_B+(up_R(i,j)-init_up_B(i,j))*(low_R(i,j)-init_low_B(i,j));
fenmu_up_B=fenmu_up_B+(up_R(i,j)-init_up_B(i,j))^2;
fenmu_low_B=fenmu_low_B+(low_R(i,j)-init_low_B(i,j))^2;
end
end
rou_R=fenzi_R/(sqrt(fenmu_up_R*fenmu_low_R));
rou_G=fenzi_G/(sqrt(fenmu_up_G*fenmu_low_G));
rou_B=fenzi_B/(sqrt(fenmu_up_B*fenmu_low_B));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 下面是计算清晰度G %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for ii=1:M-1
for jj=1:N-1
g_R=g_R+sqrt((((low_r(ii+1,jj)-low_r(ii,jj))^2+(low_r(ii,jj+1)-low_r(ii,jj))^2))/2);
g_G=g_G+sqrt((((low_g(ii+1,jj)-low_g(ii,jj))^2+(low_g(ii,jj+1)-low_g(ii,jj))^2))/2);
g_B=g_B+sqrt((((low_b(ii+1,jj)-low_b(ii,jj))^2+(low_b(ii,jj+1)-low_b(ii,jj))^2))/2);
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
四、运行结果




五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社,2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社,2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社,2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社,2015.
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/115481742
- 点赞
- 收藏
- 关注作者



评论(0)