【图像加密】基于matlab双相位编码单通道彩色图像加密【含Matlab源码 1241期】

一、双相位编码单通道彩色图像加密简介

1 前言
在国际上不断发展的新一代信息安全理论与技术的研究中，基于光学理论与方法的数据加密、隐藏和提取技术成为了一个重要的组成部分。近年来，国内外很多学者都开始从事这方面的研究，并提出了很多新方法，新技术.在这些研究中，大多是采用单色光照明，因此所恢复的图像将会失去彩色信息.
色彩是自然界的基本属性之一，图像的色彩信息在许多场合都是非常有用的，彩色图像信息的加密处理正受到越来越多的重视.在这类研究中，彩色图像通常被分成3个或多个通道，再采用和灰度图像相同的处理方法，解密时将各个通道组合起来，以恢复原来的彩色图像，这类方法常被称为多通道彩色图像处理.由于使用了多个通道，则相应的光学实现系统也就需要多个光源和多套光学元件，在增加了实验难度的同时，也增加了系统的成本，使此类方法的实用性受到限制.
本文提出一种基于双相位编码的单通道彩色图像加密方法.在该方法中， 图像首先被从RGB空间转换到HSI(色调、饱和度、强度) 空间， 再将其合并到一个通道中，采用双相位编码技术加密.其中，(强度)分量可作为双相位编码时的原始待加密图像，而编码时所用的密钥，可由H(色调)分量和S(饱和度) 分量获得.因为在HSI空间中， 色调与一个角度相对应，可以将其作为一个相位角来处理，该相位即可作为双相位编码中的相位密钥之一；而采用双随机相位加密技术对S分量加密后得到的相息图，可作为双相位编码的另一个密钥.由于仅使用一个通道对彩色图像加密，其相应的光学实现系统仅需一个光源和一套光学元件，不仅使实验难度降低，也减少了系统的成本.又因为采用双随机相位加密技术得到的S分量的相息图，在加密的过程中引进了随机相位因子，在不知密钥的情况下解密出S分量几乎不可能，从而保证了本方法的安全性.模拟实验结果证明了本文所提出方法的有效性。

2.色彩空间的转换
本文中，图像的彩色信息被转换成振幅和位相信息，以实现单通道加密.而彩色图像通常用红、绿、蓝三元组的二维矩阵来表示.为此，首先需将彩色图像用HSI表示.在RGB和HSI之间的变换公式有多种形式， 所有变换方法的基本思想都是一致的.一般而言，对

2.1 RGB 到HSI 的彩色模型转换

2.2 HSI 到RGB 的彩色模型转换

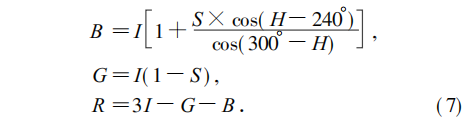
3.彩色图像的单通道加密
3.1.密钥 ——— S 分量的加密

3.2 基于双相位的单通道彩色图像加密

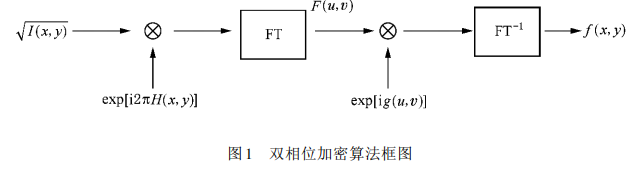
二、部分源代码

clc;close all;
I=imread('1.jpg');% 载入图像
A=im2double(I);% 将图像转为double格式
AA=rgb2hsv(A);
S=AA(:,:,2);
F=AA;
figure,imshow(A);title('彩色原始图片');% 显示图像
figure,imshow(S);title('原始');% 显示图像


[m,n,color]=size(A);
n1=exp(2j*pi*unifrnd(0,1,m,n));
n2=exp(2j*pi*unifrnd(0,1,m,n));
S=fftshift(S);

G=ifft2(fft2(S.*n1).*n2);
figure,imshow(G);title('编码');% 显示图像

function [rout,g,b] = hsv2rgb(hin,s,v)

%HSV2RGB Convert hue-saturation-value colors to red-green-blue.

%   M = HSV2RGB(H) converts an HSV color map to an RGB color map.

%   Each map is a matrix with any number of rows, exactly three columns,

%   and elements in the interval 0 to 1.  The columns of the input matrix,

%   H, represent hue, saturation and value, respectively.  The columns of

%   the resulting output matrix, M, represent intensity of red, blue and

%   green, respectively.

%

%   RGB = HSV2RGB(HSV) converts the HSV image HSV (3-D array) to the

%   equivalent RGB image RGB (3-D array).

%

%   As the hue varies from 0 to 1, the resulting color varies from

%   red, through yellow, green, cyan, blue and magenta, back to red.

%   When the saturation is 0, the colors are unsaturated; they are

%   simply shades of gray.  When the saturation is 1, the colors are

%   fully saturated; they contain no white component.  As the value

%   varies from 0 to 1, the brightness increases.

%

%   The colormap HSV is hsv2rgb([h s v]) where h is a linear ramp

%   from 0 to 1 and both s and v are all 1's.

%

%   See also RGB2HSV, COLORMAP, RGBPLOT.

 

%   Undocumented syntaxes:

%   [R,G,B] = HSV2RGB(H,S,V) converts the HSV image H,S,V to the

%   equivalent RGB image R,G,B.

%

%   RGB = HSV2RGB(H,S,V) converts the HSV image H,S,V to the 

%   equivalent RGB image stored in the 3-D array (RGB).

%

%   [R,G,B] = HSV2RGB(HSV) converts the HSV image HSV (3-D array) to

%   the equivalent RGB image R,G,B.

 

%   See Alvy Ray Smith, Color Gamut Transform Pairs, SIGGRAPH '78.

%   Copyright 1984-2011 The MathWorks, Inc. 

 

if nargin == 1 % HSV colormap

    threeD = ndims(hin)==3; % Determine if input includes a 3-D array

    if threeD

        h = hin(:,:,1); s = hin(:,:,2); v = hin(:,:,3);

    else

        h = hin(:,1); s = hin(:,2); v = hin(:,3);

    end

elseif nargin == 3

    if ~isequal(size(hin),size(s),size(v))

        error(message('MATLAB:hsv2rgb:InputSizeMismatch'));

    end

    h = hin;

else

    error(message('MATLAB:hsv2rgb:WrongInputNum'));

end    

        

h = 6.*h;

k = floor(h);

p = h-k;

t = 1-s;

n = 1-s.*p;

p = 1-(s.*(1-p));

 

% Processing each value of k separately to avoid simultaneously storing

% many temporary matrices the same size as k in memory

kc = (k==0 | k==6);

r = kc;

g = kc.*p;

b = kc.*t;

 

kc = (k==1);

r = r + kc.*n;

g = g + kc;

b = b + kc.*t;

 

kc = (k==2);

r = r + kc.*t;

g = g + kc;

b = b + kc.*p;

 

 
b = b + kc;

 

kc = (k==4);

r = r + kc.*p;

g = g + kc.*t;

b = b + kc;

 

kc = (k==5);

r = r + kc;

g = g + kc.*t;

b = b + kc.*n;

 

if nargout <= 1

     

        rout = cat(3,r,g,b);

    else

        rout = [r g b];

    end

     
else

    f = v./max([max(r(:)); max(g(:)); max(b(:))]);

    rout = f.*r;

    g = f.*g;

    b = f.*b;

end




  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
  
209
  
210
  
211
  
212
  
213
  
214
  
215
  
216
  
217
  
218
  
219
  
220
  
221
  
222
  
223
  
224
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/119869360