【车间调度】基于matlab NSGA-2算法求解多目标车间调度问题【含Matlab源码 893期】
一、车间调度简介
1 车间调度定义
车间调度是指根据产品制造的合理需求分配加工车间顺序,从而达到合理利用产品制造资源、提高企业经济效益的目的。车间调度问题从数学上可以描述为有n个待加工的零件要在m台机器上加工。问题需要满足的条件包括每个零件的各道工序使用每台机器不多于1次,每个零件都按照一定的顺序进行加工。
2 传统作业车间调度
传统作业车间带调度实例
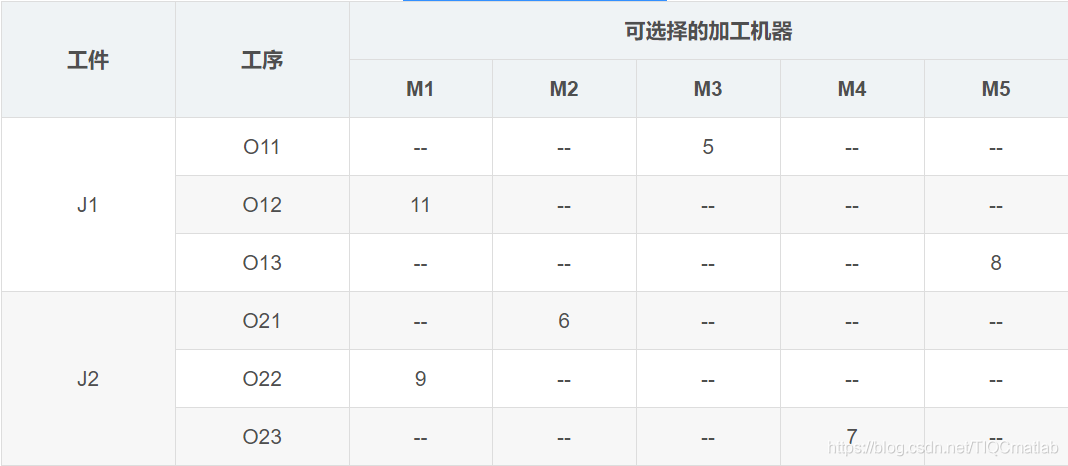
有若干工件,每个工件有若干工序,有多个加工机器,但是每道工序只能在一台机器上加工。对应到上面表格中的实例就是,两个工件,工件J1有三道工序,工序Q11只能在M3上加工,加工时间是5小时。
约束是对于一个工件来说,工序的相对顺序不能变。O11->O12->O13。每时刻,每个工件只能在一台机器上加工;每个机器上只能有一个工件。
调度的任务则是安排出工序的加工顺序,加工顺序确定了,因为每道工序只有一台机器可用,加工的机器也就确定了。
调度的目的是总的完工时间最短(也可以是其他目标)。举个例子,比如确定了O21->O22->O11->O23->O12->O13的加工顺序之后,我们就可以根据加工机器的约束,计算出总的加工时间。
M2加工O21消耗6小时,工件J2当前加工时间6小时。
M1加工O22消耗9小时,工件J2当前加工时间6+9=15小时。
M3加工O11消耗5小时,工件J1当前加工时间5小时。
M4加工O23消耗7小时,工件J2加工时间15+7=22小时。
M1加工O12消耗11小时,但是要等M1加工完O22之后才开始加工O12,所以工件J1的当前加工时间为max(5,9)+11=20小时。
M5加工O13消耗8小时,工件J2加工时间20+8=28小时。
总的完工时间就是max(22,28)=28小时。
2 柔性作业车间调度
柔性作业车间带调度实例(参考自高亮老师论文
《改进遗传算法求解柔性作业车间调度问题》——机械工程学报)
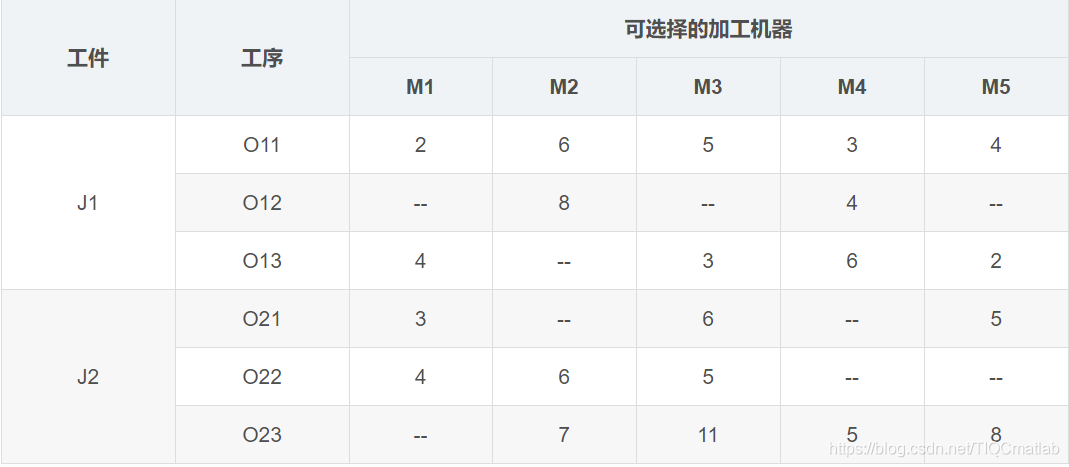
相比于传统作业车间调度,柔性作业车间调度放宽了对加工机器的约束,更符合现实生产情况,每个工序可选加工机器变成了多个,可以由多个加工机器中的一个加工。比如上表中的实例,J1的O12工序可以选择M2和M4加工,加工时间分别是8小时和4小时,但是并不一定选择M4加工,最后得出来的总的完工时间就更短,所以,需要调度算法求解优化。
相比于传统作业车间,柔性车间作业调度的调度任务不仅要确定工序的加工顺序,而且需要确定每道工序的机器分配。比如,确定了O21->O22->O11->O23->O12->O13的加工顺序,我们并不能相应工序的加工机器,所以还应该确定对应的[M1、M3、M5]->[M1、M2、M3]->[M1、M2、M3、M4、M5]->[M2、M3、M4、M5]->[M2、M4]->[M1、M3、M4、M5]的机器组合。调度的目的还是总的完工时间最短(也可以是其他目标,比如机器最大负荷最短、总的机器负荷最短)
3 NSGA2遗传算法的流程图
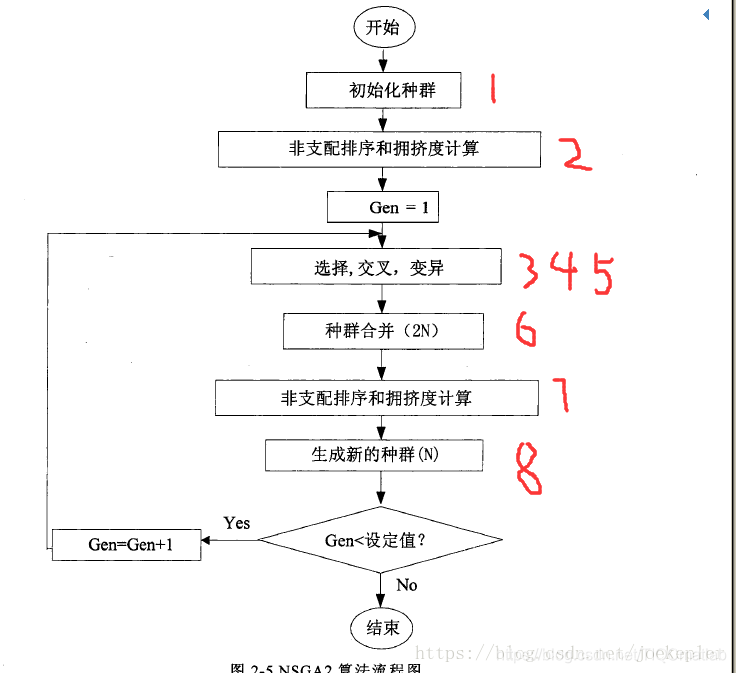
二、部分源代码
clc;
clear;
close all;
%% Problem Definition
load CastingData Jm T JmNumber DeliveryTime IntervalTime
CostFunction=@(x,Jm ,T ,JmNumber ,DeliveryTime, IntervalTime) MyCost(x,Jm ,T ,JmNumber ,DeliveryTime, IntervalTime);
nVar=3;
VarSize=[1 nVar];
VarMin=-4;
VarMax= 4;
pfmax=0.9;
pfmin=0.2;
VarRange=[VarMin VarMax];
%% NSGA-II Parameters
MaxIt=500;
nPop=50;
pCrossover=0.8;
nCrossover=round(pCrossover*nPop/2)*2;
pMutation=0.3;
nMutation=round(pMutation*nPop);
mu=0.3;
%% Initialization
tic;
% PNumber 铸件个数 MNumber 工序个数数组 每个工件对应的工序数量有可能不同
PNumber=size(Jm,1);
trace=zeros(2, MaxIt); %寻优结果的初始值
MNumber=[];
for i=1:size(Jm,1)
sumTemp=0;
for j=1:size(Jm,2)
if(length(Jm{i,j}))>0
sumTemp=sumTemp+1;
end
end
MNumber=[MNumber,sumTemp];
end
WNumber=sum(MNumber); %工序总个数
%% 初始化
Number=MNumber;
D=WNumber*2; %粒子群维度
empty_individual.Position=[];
empty_individual.Cost=[];
empty_individual.Rank=[];
empty_individual.CrowdingDistance=[];
empty_individual.DominatedCount=[];
empty_individual.DominationSet=[];
% 初始化种群
pop=repmat(empty_individual,nPop,1);
for i=1:nPop
WPNumberTemp=Number;
if i<nPop/2
for j=1:WNumber
%随机产成工序
val=unidrnd(PNumber);
while WPNumberTemp(val)==0
val=unidrnd(PNumber);
end
%第一层代码表示工序
pop(i).Position(j)=val; %随机初始化位置
WPNumberTemp(val)=WPNumberTemp(val)-1;
%第2层代码表示机器
TempT=T{val,MNumber(val)-WPNumberTemp(val)};
% 机器加工时间最少初始化
%[~,minTimeIndex]=min(TempT);
% 随机机器初始化
mindex=unidrnd(length(TempT));
%随机产成工序机器
pop(i).Position(j+WNumber)=mindex;
end
else
for j=1:WNumber
%随机产成工序
val=unidrnd(PNumber);
while WPNumberTemp(val)==0
val=unidrnd(PNumber);
end
%第一层代码表示工序
pop(i).Position(j)=val; %随机初始化位置
WPNumberTemp(val)=WPNumberTemp(val)-1;
%第2层代码表示机器
TempT=T{val,MNumber(val)-WPNumberTemp(val)};
% 机器加工时间最少初始化
[~,minTimeIndex]=min(TempT);
% 随机机器初始化
%mindex=unidrnd(length(TempT));
%随机产成工序机器
pop(i).Position(j+WNumber)=minTimeIndex;
end
end
end
for i=1:nPop
pop(i).Cost=CostFunction(pop(i).Position,Jm ,T ,JmNumber ,DeliveryTime, IntervalTime);
end
% Non-dominated Sorting
[pop ,F]=NonDominatedSorting(pop);
% Calculate Crowding Distances
pop=CalcCrowdingDistance(pop,F);
%% NSGA-II Loop
for it=1:MaxIt
% Crossover
popc=repmat(empty_individual,nCrossover,1);
pf=pfmax-(pfmax-pfmin)*it/MaxIt;
for k=1:nCrossover
i1=BinaryTournamentSelection(pop);
i2=BinaryTournamentSelection(pop);
% [popc(k,1).Position, popc(k,2).Position]=Crossover(pop(i1).Position,pop(i2).Position,VarRange);
popc(k,1).Position= CrossParticle(pop(i1).Position,pop(i2).Position,Jm,pf);
popc(k,1).Cost=CostFunction(popc(k,1).Position,Jm ,T ,JmNumber ,DeliveryTime, IntervalTime);
end
popc=popc(:);
% Mutation
popm=repmat(empty_individual,nMutation,1);
for k=1:nMutation
i=BinaryTournamentSelection(pop);
if rand()<mu
popm(k).Position=Swap(pop(i).Position,Jm);
popm(k).Cost=CostFunction(popm(k).Position,Jm ,T ,JmNumber ,DeliveryTime, IntervalTime);
else
popm(k).Position=pop(i).Position;
popm(k).Cost=pop(i).Cost;
end
end
% Merge Pops
pop=[pop
popc
popm];
% Non-dominated Sorting
[pop, F]=NonDominatedSorting(pop);
% Calculate Crowding Distances
pop=CalcCrowdingDistance(pop,F);
% Sort Population
pop=SortPopulation(pop);
% Delete Extra Individuals
pop=pop(1:nPop);
% Non-dominated Sorting
[pop, F]=NonDominatedSorting(pop);
% Calculate Crowding Distances
pop=CalcCrowdingDistance(pop,F);
% Plot F1
PF=pop(F{1});
PFCosts=[PF.Cost];
popCosts=[pop.Cost];
firstObj=popCosts(1,:);
secondObj=popCosts(2,:);
trace(1, it)=min(firstObj);
trace(2, it)=min(secondObj);
% 画图
fig=figure(1);
set(fig,'NAME','NSGA-MultiObj');
plot(PFCosts(1,:),PFCosts(2,:),'ro');
xlabel('间隔时间拖时');
ylabel('交货延期');
% Show Iteration Information
disp(['Iteraion ' num2str(it) ': Number of F1 Members = ' num2str(numel(PF))]);
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
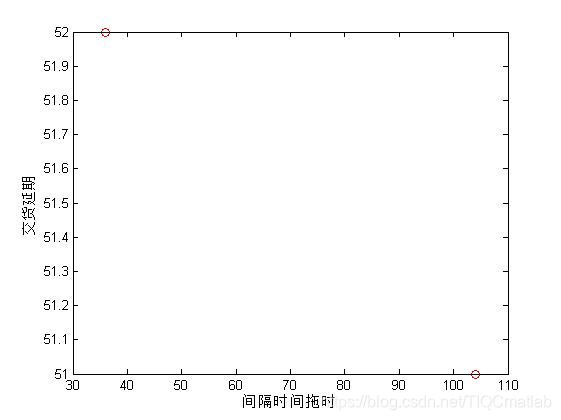
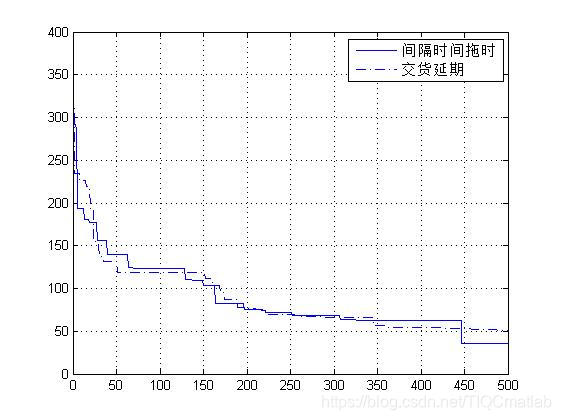
三、运行结果

四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/116905027
- 点赞
- 收藏
- 关注作者


评论(0)