【生产调度】基于matlab免疫算法求解生产调度零等待问题【含Matlab源码 1178期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【生产调度】基于matlab免疫算法求解生产调度零等待问题【含Matlab源码 1178期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、免疫算法简介

1引言
“Immune”(免疫)一词是从拉丁文衍生而来的。很早以前，人们就注意到传染病患者痊愈后，对该病会有不同程度的免疫力。在医学上，免疫是指机体接触抗原性异物的一种生理反应。1958年澳大利亚学者Burnet率先提出了与免疫算法(Immune Algorithm， I A) 相关的理论――克隆选择原理[1] 。1973年Jer ne提出免疫系统的模型[2] ， 他基于Burnet的克隆选择学说， 开创了独特型网络理论， 给出了免疫系统的数学框架，并采用微分方程建模来仿真淋巴细胞的动态变化。
1986年Farm al等人基于免疫网络学说理论构造出的免疫系统的动态模型，展示了免疫系统与其他人工智能方法相结合的可能性，开创了免疫系统研究的先河。他们先利用一组随机产生的微分方程建立起
人工免疫系统，再通过采用适应度阈值过滤的方法去掉方程组中那些不合适的微分方程，对保留下来的微分方程则采用交叉、变异、逆转等遗传操作产生新的微分方程，经过不断的迭代计算，直到找到最佳的一组微分方程为止。
从此以后，对免疫算法的研究在国际上引起越来越多学者的兴趣。几十年来，与之相关的研究成果已经涉及非线性最优化、组合优化、控制工程、机器人、故障诊断、图像处理等诸多领域[3-6].免疫算法是模仿生物免疫机制，结合基因的进化机理，人工构造出的一种新型智能优化算法。它具有一般免疫系统的特征，采用群体搜索策略，通过迭代计算，最终以较大的概率得到问题的最优解。相比较于其他算法，免疫算法利用自身产生多样性和维持机制的特点，保证了种群的多样性，克服了一般寻优过程(特别是多峰值的寻优过程)中不可避免的“早熟”问题，可以求得全局最优解。免疫算法具有自适应性、随机性、并行性、全局收敛性、种群多样性等优点。

2 免疫算法理论
生物免疫系统是一个复杂的自适应系统。免疫系统能够识别出病原体，具有学习、记忆和模式识别能力，因此可以借鉴其信息处理机制来解决科学和工程问题。免疫算法正是基于生物免疫系统识别外部
病原体并产生抗体对抗病原体的学习机制而提出的，由此诞生了基于免疫原理的智能优化方法研究这一新的研究方向。

2.1生物免疫系统
传统免疫是指机体抗感染的防御能力，而现代免疫则指机体免疫系统识别和排除抗原性异物，从而维持机体生理平衡和稳定的功能。免疫是机体的一种生理反应，当病原体(即抗原)进入人体时，这些抗原将刺激免疫细胞(淋巴B细胞、T细胞)产生一种抵抗该病原生物的特殊蛋白质一一抗体。抗体能将该病原生物消灭，并在将病原生物消灭之后，仍存留在人体内。当同样的病原生物再次侵入人体时，该
病原生物就会很快地被体内存留的抗体消灭[7].
免疫学相关概念
免疫
免疫是指机体对自身和异体识别与响应过程中产生的生物学效应的总和，正常情况下是一种维持机体循环稳定的生理性功能。生物机体识别异体抗原，对其产生免疫响应并清除；机体对自身抗原不产生
免疫响应。
抗原
抗原是一种能够刺激机体产生免疫应答并能与应答产物结合的物质。它不是免疫系统的有机组成部分，但它是启动免疫应答的始动因素。
抗体
抗体是一种能够进行特异识别和清除抗原的免疫分子，其中具有抗细菌和抗毒素免疫功能的球蛋白物质，故抗体也称免疫球蛋白分子，它是由B细胞分化成的浆细胞所产生的。
T细胞和B细胞
T细胞和B细胞是淋巴细胞的主要组成部分。B细胞受到抗原刺激后，可增殖分化为大量浆细胞，而浆细胞具有合成和分泌抗体的功能。但是，B细胞不能识别大多数抗原，必须借助能识别抗原的辅助性
T细胞来辅助B细胞活化，产生抗体。
生物免疫系统机理
生物免疫系统是由免疫分子、免疫组织和免疫细胞组成的复杂系统。这些组成免疫系统的组织和器官分布在人体各处，用来完成各种免疫防卫功能，它们就是人们熟知的淋巴器官和淋巴组织。
免疫识别
免疫识别是免疫系统的主要功能，识别的本质是区分“自己”和“非己”。免疫识别是通过淋巴细胞上的抗原受体与抗原的结合来实现的。
免疫学习
免疫识别过程同时也是一个学习的过程，学习的结果是免疫细胞的个体亲和度提高、群体规模扩大，并且最优个体以免疫记忆的形式得到保存。
免疫记忆
当免疫系统初次遇到一种抗原时，淋巴细胞需要一定的时间进行调整以更好地识别抗原，并在识别结束后以最优抗体的形式保留对该抗原的记忆信息。而当免疫系统再次遇到相同或者结构相似的抗原
时，在联想记忆的作用下，其应答速度大大提高。
克隆选择
免疫应答和免疫细胞的增殖在一个特定的匹配阈值之上发生。当淋巴细胞实现对抗原的识别，B细胞被激活并增殖复制产生克隆B细胞，随后克隆细胞经历变异过程，产生对抗原具有特异性的抗体。
个体多样性
根据免疫学知识，免疫系统有100多种不同的蛋白质，但外部潜在的抗原和待识别的模式种类有1000多种。要实现数量级远远大于自身的抗原识别，需要有效的多样性个体产生机制。抗体多样性的生物
机制主要包括免疫受体库的组合式重整、体细胞高频突变以及基因转换等。
分布式和自适应性
免疫系统的分布式特性首先取决于病原的分布式特性，即病原是分散在机体内部的。由于免疫应答机制是通过局部细胞的交互作用而不存在集中控制，所以免疫系统的分布式进一步增强了其自适应特
性。所有这些免疫系统的重要信息处理特点为信息和计算领域的应用提供了有力的支撑。

2.2免疫算法概念
免疫算法是受生物免疫系统的启发而推出的一种新型的智能搜索算法。它是一种确定性和随机性选择相结合并具有“勘探”与“开采”能力的启发式随机搜索算法。免疫算法将优化问题中待优化的问题对应免疫应答中的抗原，可行解对应抗体(B细胞)，可行解质量对应免疫细胞与抗原的亲和度。如此则可以将优化问题的寻优过程与生物免疫系统识别抗原并实现抗体进化的过程对应起来，将生物免疫应答中的进化过程抽象为数学上的进化寻优过程，形成一种智能优化算法。
免疫算法是对生物免疫系统机理抽象而得的，算法中的许多概念和算子与免疫系统中的概念和免疫机理存在着对应关系。免疫算法与生物免疫系统概念的对应关系如表1所示。由于抗体是由B细胞产生
的，在免疫算法中对抗体和B细胞不做区分，都对应为优化问题的可行解。
表1免疫算法与生物免疫系统概念的对应关系

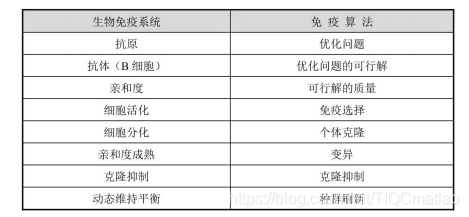
根据上述的对应关系，模拟生物免疫应答的过程形成了用于优化计算的免疫算法。算法主要包含以下几大模块：
(1)抗原识别与初始抗体产生。根据待优化问题的特点设计合适的抗体编码规则，并在此编码规则下利用问题的先验知识产生初始抗体种群。
(2)抗体评价。对抗体的质量进行评价，评价准则主要为抗体亲和度和个体浓度，评价得出的优质抗体将进行进化免疫操作，劣质抗体将会被更新。
(3)免疫操作。利用免疫选择、克隆、变异、克隆抑制、种群刷新等算子模拟生物免疫应答中的各种免疫操作，形成基于生物免疫系统克隆选择原理的进化规则和方法，实现对各种最优化问题的寻优搜
索。

2.3免疫算法的特点
免疫算法是受免疫学启发，模拟生物免疫系统功能和原理来解决复杂问题的自适应智能系统，它保留了生物免疫系统所具有的若干特点[8]，包括：
(1)全局搜索能力。模仿免疫应答过程提出的免疫算法是一种具有全局搜索能力的优化算法，免疫算法在对优质抗体邻域进行局部搜索的同时利用变异算子和种群刷新算子不断产生新个体，探索可行解
区间的新区域，保证算法在完整的可行解区间进行搜索，具有全局收敛性能。
(2)多样性保持机制。免疫算法借鉴了生物免疫系统的多样性保持机制，对抗体进行浓度计算，并将浓度计算的结果作为评价抗体个体优劣的一个重要标准：它使浓度高的抗体被抑制，保证抗体种群具有很好的多样性，这也是保证算法全局收敛性能的一个重要方面。
(3)鲁棒性强。基于生物免疫机理的免疫算法不针对特定问题，而且不强调算法参数设置和初始解的质量，利用其启发式的智能搜索机制，即使起步于劣质解种群，最终也可以搜索到问题的全局最优解，对问题和初始解的依赖性不强，具有很强的适应性和鲁棒性。
(4)并行分布式搜索机制。免疫算法不需要集中控制，可以实现并行处理。而且，免疫算法的优化进程是一种多进程的并行优化，在探求问题最优解的同时可以得到问题的多个次优解，即除找到问题的最佳解决方案外，还会得到若干较好的备选方案，尤其适合于多模态的优化问题。

2.4免疫算法算子
与遗传算法等其他智能优化算法类似，免疫算法的进化寻优过程也是通过算子来实现的。免疫算法的算子包括：亲和度评价算子、抗体浓度评价算子、激励度计算算子、免疫选择算子、克隆算子、变异
算子、克隆抑制算子和种群刷新算子等[9].由于算法的编码方式可能为实数编码、离散编码等，不同编码方式下的算法算子也会有所不同。
亲和度评价算子
亲和度表征免疫细胞与抗原的结合强度，与遗传算法中的适应度类似。亲和度评价算子通常是一个函数aff(x) ：SER， 其中S为问题的可行解区间，R为实数域。函数的输入为一个抗体个体(可行解)，输出即为亲和度评价结果。亲和度的评价与问题具体相关，针对不同的优化问题，应该在理解问题实质的前提下，根据问题的特点定义亲和度评价函数。通常函数优化问题可以用函数值或对函数值的简单处理(如取倒数、相反数等)作为亲和度评价，而对于组合优化问题或应用中更为复杂的优化问题，则需要具体问题具体分析。
抗体浓度评价算子
抗体浓度表征抗体种群的多样性好坏。抗体浓度过高意味着种群中非常类似的个体大量存在，则寻优搜索会集中于可行解区间的一个区域，不利于全局优化。因此优化算法中应对浓度过高的个体进行抑
制，保证个体的多样性。
抗体浓度通常定义为：


免疫选择算子
免疫选择算子根据抗体的激励度确定选择哪些抗体进入克隆选择操作。在抗体群中激励度高的抗体个体具有更好的质量，更有可能被选中进行克隆选择操作，在搜索空间中更有搜索价值。
克隆算子

离散编码算法变异算子
离散编码算法以二进制编码为主，其变异策略是从变异源抗体串中随机选取几位元，改变位元的取值(取反)，使其落在离散空间变异源的邻域。
克隆抑制算子
克隆抑制算子用于对经过变异后的克隆体进行再选择，抑制亲和度低的抗体，保留亲和度高的抗体进入新的抗体种群。在克隆抑制的过程中，克隆算子操作的源抗体与克隆体经变异算子作用后得到的临
时抗体群共同组成一个集合，克隆抑制操作将保留此集合中亲和度最高的抗体，抑制其他抗体。
由于克隆变异算子操作的源抗体是种群中的优质抗体，而克隆抑制算子操作的临时抗体集合中又包含了父代的源抗体，因此在免疫算法的算子操作中隐含了最优个体保留机制。
种群刷新算子
种群刷新算子用于对种群中激励度较低的抗体进行刷新，从抗体种群中删除这些抗体并以随机生成的新抗体替代，有利于保持抗体的多样性，实现全局搜索，探索新的可行解空间区域。

3免疫算法种类
3.1克隆选择算法
Castro提出了基于免疫系统的克隆选择理论的克隆选择算法[10] ，该算法是模拟免疫系统学习过程的进化算法。免疫应答产生抗体是免疫系统的学习过程，抗原被一些与之匹配的B细胞识别，这些B细胞分裂，产生的子B细胞在母细胞的基础上发生变化，以寻求与抗原匹配更好的B细胞，与抗原匹配更好的子B细胞再分裂……如此循环往复，最后找到与抗原完全匹配的B细胞，B细胞变成浆细胞产生抗体，这一过程就是克隆选择过程，克隆选择算法模拟这一过程进行优化。
3.2免疫遗传算法
Chun等人提出了一种免疫算法， 实质上是改进的遗传算法[11] .根据体细胞和免疫网理论改进了遗传算法的选择操作，从而保持了群体的多样性，提高算法的全局寻优能力。通过在算法中加入免疫记忆
功能，提高了算法的收敛速度。免疫遗传算法把抗原看作目标函数，将抗体看作问题的可行解，抗体与抗原的亲和度看作可行解的适应度。免疫遗传算法引入了抗体浓度的概念，并用信息熵来描述，表示群体中相似可行解的多少。免疫遗传算法根据抗体与抗原的亲和度和抗体的浓度进行选择操作，亲和度高且浓度小的抗体选择率大，这样就抑制了群体中浓度高的抗体，保持了群体的多样性。
3.3反向选择算法
免疫系统中的T细胞在胸腺中发育，与自身蛋白质发生反应的未成熟T细胞被破坏掉，所以成熟的T细胞具有忍耐自身的性质，不与自身蛋白质发生反应，只与外来蛋白质产生反应，以此来识别“自己”与“非己”，这就是所谓的反向选择原理。Forrest基于反向选择原理提出了反向选择算法， 用于进行异常检
测[12].算法主要包括两个步骤：首先，产生一个检测器集合，其中每一个检测器与被保护的数据不匹配：其次，不断地将集合中的每一个检测器与被保护数据相比较，如果检测器与被保护数据相匹配，则判定数据发生了变化。

3.4疫苗免疫算法
焦李成等人基于免疫系统的理论提出了基于疫苗的免疫算法[13].该算法是在遗传算法中加入免疫算子，以提高算法的收敛速度并防止群体退化。免疫算子包括疫苗接种和免疫选择两个部分，前者为了提高亲和度，后者为了防止种群退化。理论分析表明这种免疫算法是收敛的。
疫苗免疫算法的基本步骤是：随机产生NP个个体构成初始父代群体；根据先验知识抽取疫苗；计算当前父代种群所有个体的亲和度，并进行停止条件的判断：对当前的父代群体进行变异操作，生成子代
群体：对子代群体进行疫苗接种操作，得到新种群；对新群体进行免疫选择操作，得到新一代父本，并进入免疫循环。

4免疫算法流程
目前还没有统一的免疫算法及框图，下面介绍一种含有4.2.4节免疫算子的算法流程，分为以下几个步骤：
(1)首先进行抗原识别，即理解待优化的问题，对问题进行可行性分析，提取先验知识，构造出合适的亲和度函数，并制定各种约束条件。
(2)然后产生初始抗体群，通过编码把问题的可行解表示成解空间中的抗体，在解的空间内随机产生一个初始种群。
(3)对种群中的每一个可行解进行亲和度评价。
(4)判断是否满足算法终止条件：如果满足条件，则终止算法寻优过程，输出计算结果：否则，继续寻优运算。
(5)计算抗体浓度和激励度。
(6)进行免疫处理，包括免疫选择、克隆、变异和克隆抑制。

免疫选择：根据种群中抗体的亲和度和浓度计算结果选择优质抗体，使其活化：
克隆：对活化的抗体进行克隆复制，得到若干副本；变异：对克隆得到的副本进行变异操作，使其发生亲和度突变；
克隆抑制：对变异结果进行再选择，抑制亲和度低的抗体，保留亲和度高的变异结果。
(7)种群刷新，以随机生成的新抗体替代种群中激励度较低的抗体，形成新一代抗体，转步骤(3)。
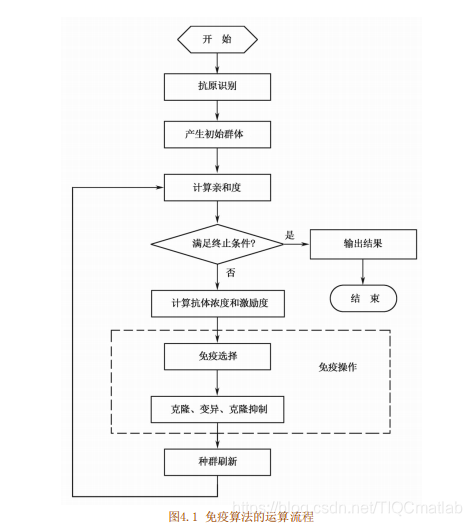
免疫算法运算流程如图1所示。

免疫算法中的进化操作是采用了基于免疫原理的进化算子实现的，如免疫选择、克隆、变异等。而且算法中增加了抗体浓度和激励度的计算，并将抗体浓度作为评价个体质量的一个标准，有利于保持个体多样性，实现全局寻优。

5 关键参数说明
下面介绍一下免疫算法的主要参数，它在程序设计与调试中起着至关重要的作用。免疫算法主要包括以下关键参数：
抗体种群大小NP
抗体种群保留了免疫细胞的多样性，从直观上看，种群越大，免疫算法的全局搜索能力越好，但是算法每代的计算量也相应增大。在大多数问题中，NP取10~100较为合适，一般不超过200。
免疫选择比例
免疫选择的抗体的数量越多，将产生更多的克隆，其搜索能力越强，但是将增加每代的计算量。一般可以取抗体种群大小NP的10%~50%。
抗体克隆扩增的倍数
克隆的倍数决定了克隆扩增的细胞的数量，从而决定了算法的搜索能力，主要是局部搜索能力。克隆倍数数值越大，局部搜索能力越好，全局搜索能力也有一定提高，但是计算量也随之增大，一般取5~
10倍。
种群刷新比例
细胞的淘汰和更新是产生抗体多样性的重要机制，因而对免疫算法的全局搜索能力产生重要影响。每代更新的抗体一般不超过抗体种群的50%。
最大进化代数G
最大进化代数G是表示免疫算法运行结束条件的一个参数，表示免疫算法运行到指定的进化代数之后就停止运行，并将当前群体中的最佳个体作为所求问题的最优解输出。一般6取100~500。
1.1最短路径规划
路径规划是指，在具有障碍物的环境中，按照一定的评价标准，寻找一条从起始到目标状态的无碰撞路径。最短路径规划向题是图论研究中的一个经典算法同题，其目的是寻找图(由结点和路径组成的)中两结点之间的最短路径。
该间题的具体形式如下：
(1)确定起点的最短路径问题:已知起始结点，求最短路径的问题。
(2)确定终点的最短路径问题:与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
(3)确定起点终点的最短路径问题:已知起点和终点，求两结点之间的最短路径。
(4)全局最短路径问题:求图中所有的最短路径。
设P(u，v)是地图中从u到v的路径，则该路径上的边权之和称为该路径的权，记为现w§。从u到v的路径中权最小者P*(u，v)称为u到v的最短路径。

三、部分源代码

clear;
% RUN=10;
% for run=1:RUN
%初始化
generation=0;
%机器数
m=5;
%工件数
n=10;
%初始抗体数
Pop_size=40;
N=Pop_size;
%替换抗体数
Ns=30;
%克隆选择概率
Pa=0.7;
%细胞克隆数
M=80;
%浓度，克隆抑制半径
Py=0.7;
%激励系数
Pb=100;
%变异概率
Pz=0.6;
Pc=0.3;
Ps=0.3;
Pi=0.3;
Pm=0.05;
%浓度选择率
Pn=0.7;
% %反馈概率
% Pr=1;
%迭代次数
IterativeTime=60;
OperationTime=[25 17 41  74 37  72  11 31  32  27 
               15 41 155 12 95  34  77 39  92  114  
               12 22 83  24 72  62  31 141 42  21  
               40 36 121 48 52  32  26 56  74  90 
               60 58 160 78 153 162 32 79  102 52 ];%产生初始种群
P=zeros(N,n);
for i=1:N
    for j=1:n
        P(i,:)=randperm(n);
    end
end
%计算目标值
[MakeP,CL,ST]=calculate(m,n,N,P,OperationTime);
%计算亲和度
Aff=Affcalculate(N,MakeP);
%计算相似度
Ayy=Aycalculate(P,n,N);
%计算各抗体浓度
aa=0;
for i=1:N
    for j=1:N
        if Ayy(i,j)>Py
            aa=aa+1;
        end
    end
    Nong(1,i)=aa/N;
    aa=0;
end
%找出最好个体
bestmax=MakeP(1,1);
for i=1:N
    if bestmax>=MakeP(1,i)
        bestmax=MakeP(1,i);
        positionP=i;
    end
end
%最好解对应的最好个体
best=P(positionP,:);
bestStarttime=ST(:,:,positionP);
bestEndtime=CL(:,:,positionP);
Best=best;
BestStarttime=bestStarttime;
BestEndtime=bestEndtime;
Bestmax=bestmax;
Makespan=zeros(1,IterativeTime);
BestMake=zeros(1,IterativeTime);
Aff_PP=zeros(1,IterativeTime);
%保存上一代种群
Last=P;
generation=0;
while(generation<IterativeTime)
       generation=generation+1;
   Makespan(1,generation)=bestmax;
   BestMake(1,generation)=Bestmax;
   %按照亲和度大小进行排序（克隆选择）
   [f1,index1]=sort(Aff,'descend');%降序排列
   N1=Pa*N;
   B=zeros(N1,n);
   for i=1:N1
       for j=1:n
           B(i,:)=P(index1(i),:);
       end
   end
   ff1=0;
   for i=1:N1
       ff1=ff1+f1(i);
   end
   %按照各抗体的亲和度大小对B中的抗体进行克隆
   MM=0;
   for i=1:N1
       Mn(i)=round(M*f1(i)/ff1);%将每个抗体需要克隆的个体数存放在Mn(i)中
       MM=MM+Mn(i);%实际克隆的数目；
   end
   %开始克隆，种群数为MM（细胞克隆）
   sum=0;
   C=zeros(MM,n);
   for k=1:N1
       for j=1:Mn(k)
           C_Swarm((sum+j),:)=B(k,:);
       end
       sum=sum+Mn(k);
   end
   for i=1:MM
       C(i,:)=C_Swarm(i,:);
   end
   %计算克隆后的亲和度
  [MakePC,CL,ST]=calculateC(m,n,MM,C,OperationTime);
   Aff_MM1=Aff_MM1calculate(MM,MakePC);
   C_Swarm2=C;
   %克隆重组
   if rand(1)<Pz
       for i=1:round(MM/2)
           Tw=zeros(2,n);
           Tw(1,:)=C(i,:);
           Tw(2,:)=C(MM-i+1,:);
           %随机产生一个交叉位
           j_bit=0;
           for s=0:n-1
               if (((rand(1,1)*n)<s+1)&((rand(1,1)*n)>=s))
                   j_bit=s;
               end
           end
           j=j_bit+1;
           for k=1:n
               if Tw(1,k)~=Tw(2,1:j_bit);
                   Tw(2,j)=Tw(1,k);
                   j=j+1;
               end
           end
           j=j_bit+1;
           for k=1:n
           if Tw(2,k)~=Tw(1,1:j_bit);
               Tw(1,j)=Tw(2,k); 
               j=j+1;
           end
           end
       C(i,:)=Tw(1,:);
       C(MM-i+1,:)=Tw(2,:);
       end
   end
 %计算变异后各抗体亲和度
[MakePC,CL,ST]=calculateC(m,n,MM,C,OperationTime);
Aff_MM3=Aff_MM3calculate(MM,MakePC);
 %变异前后进行比较，确定是否删除
 for i=1:MM
    if Aff_MM1(1,i)>Aff_MM3(1,i)
        C(i,:)=C_Swarm2(i,:);
        Aff_MM1(1,i)=Aff_MM3(1,i);
    end
end
   %基因突变
   %按照一定的交换概率Pc交换两个点之间的基因；
   for i=1:MM
       if rand(1)<Pc
           C(i,:)=change(C(i,:),n);
       end
   %按照一定的概率Pi逆序排列两个点之间的基因；	
	if rand(1)<Pi
        C(i,:)=inverse(C(i,:),n);
    end

 %按照一定的概率Ps移位两个点之间的基因段;
	if rand(1)<Ps
        C(i,:)=shift(C(i,:),n);
    end
end     
%克隆抑制
%计算突变后各抗体的亲和度
[MakePC,CL,ST]=calculateC(m,n,MM,C,OperationTime);
Aff_MM2=Aff_MM2calculate(MM,MakePC);
%将变异前后的抗体进行比较，来决定是否进行删除操作；
for i=1:MM
    if Aff_MM1(1,i)>Aff_MM2(1,i)
        C(i,:)=C_Swarm(i,:);
        Aff_MM1(1,i)=Aff_MM2(1,i);
    end
end
% C_Swarm2=C;
% %按照一定的概率对抗体一点或多点进行变异；
% for i=1:MM
%        if rand(1)<Pm
%            C(i,:)=mutation(C(i,:),n);
%        end
% end
%  %计算变异后各抗体亲和度
% [MakePC,CL,ST]=calculateC(m,n,MM,C,OperationTime);
% Aff_MM3=Aff_MM3calculate(MM,MakePC);
%  %变异前后进行比较，确定是否删除
%  for i=1:MM
%     if Aff_MM1(1,i)>Aff_MM3(1,i)
%         C(i,:)=C_Swarm2(i,:);
%         Aff_MM1(1,i)=Aff_MM3(1,i);
%     end
% end
%计算各抗体的相似度，并对相似度高的个体去除
 Ayy_MM=Aycalculate(C,n,MM);
 aa=0;
Nong_MM=zeros(1,MM);
for i=1:MM
    for j=1:MM
        if Ayy_MM(i,j)>Py
            aa=aa+1;
        end
    end
    Nong_MM(1,i)=aa/MM;
    aa=0;
end
fn1=zeros(MM);
indexfn=zeros(MM);
Nc=round(Pn*MM);
D=zeros(Nc,n);
[fn1,indexfn]=sort(Nong_MM);
for i=1:Nc
            D(i,:)=C(indexfn(i),:);
            Nong_D(1,i)=Nong_MM(1,indexfn(i));
            Aff_D(1,i)=Aff_MM1(1,indexfn(i));
end
%计算D中抗体的亲和度
NNc=N+Nc;
%合并P和D两个抗体群，得到NNc个合体的抗体群E；

        E(i,:)=D(i,:);
        Aff_E(1,i)=Aff_D(1,i);
        Nong_E(1,i)=Nong_D(1,i);
    end
    if i>Nc
       E(i,:)=P(i-Nc,:);
       Aff_E(1,i)=Aff(1,i-Nc); 
       Nong_E(1,i)=Nong(1,i-Nc);
    end
end
%计算激励度
for i=1:NNc
    act(1,i)= Aff_E(1,i)*exp(-Nong_E(1,i)/Pb);
end
%各抗体亲和力排序
f_AE=zeros(NNc);
index3=zeros(NNc);
[f_AE,index3]=sort(Aff_E,'descend');
%排序，选出激励度最高且不相同的前N个抗体群F
[f_E,index2]=sort(act,'descend');
 inumber=2;
    for i=1:NNc-1
    if f_E(i)>f_E(i+1)
    F(inumber,:)=E(index2(i),:);
    inumber=inumber+1;
    end
    if inumber==N+1

    end
F(1,:)=E(index3(1),:);
%计算抗体的亲和度，并排序
%计算目标值
[MakeP,CL,ST]=calculate(m,n,N,F,OperationTime);
%计算亲和度
Aff_F=Affcalculate(N,MakeP);
[f_F,index4]=sort(Aff_F,'descend');
for i=1:N
    G(i,:)=F(index4(i),:);
end

%随机产生的抗体G替代F中的激励度最后的0.1*N个抗体
% if generation<50
    for i=1:Ns

bbb=0;
for i=1:N
    bbb=bbb+MakeP(1,i);
end
Make_P=bbb/N;
%找出最好个体
bestmax=MakeP(1,1);
for i=1:N
    if bestmax>=MakeP(1,i)
        bestmax=MakeP(1,i);
        positionP=i;
    end
end
%最好解对应的最好个体
best=P(positionP,:);
bestStarttime=ST(:,:,positionP);
bestEndtime=CL(:,:,positionP);
%找到全局最好解
if bestmax<Bestmax
Bestmax=bestmax;
BestStarttime=bestStarttime;
BestEndtime=bestEndtime;
Best=best;
end
 Aff_PP(1,generation)=Aff_P;
 Make_PP(1,generation)=Make_P;
end
BestStarttime1=BestStarttime(:,:,1);
BestEndtime1=BestEndtime(:,:,1);
% 画Gantte图
picturegantchart(m,n,Bestmax,Best,BestStarttime1,BestEndtime1);
figure(2);
plot(Makespan);
figure(3);
plot(BestMake);
figure(4);
plot(Aff_PP);
figure(5);
plot(Make_PP);
% seg(run,1)=Bestmax;
% end
%     


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
  
169
  
170
  
171
  
172
  
173
  
174
  
175
  
176
  
177
  
178
  
179
  
180
  
181
  
182
  
183
  
184
  
185
  
186
  
187
  
188
  
189
  
190
  
191
  
192
  
193
  
194
  
195
  
196
  
197
  
198
  
199
  
200
  
201
  
202
  
203
  
204
  
205
  
206
  
207
  
208
  
209
  
210
  
211
  
212
  
213
  
214
  
215
  
216
  
217
  
218
  
219
  
220
  
221
  
222
  
223
  
224
  
225
  
226
  
227
  
228
  
229
  
230
  
231
  
232
  
233
  
234
  
235
  
236
  
237
  
238
  
239
  
240
  
241
  
242
  
243
  
244
  
245
  
246
  
247
  
248
  
249
  
250
  
251
  
252
  
253
  
254
  
255
  
256
  
257
  
258
  
259
  
260
  
261
  
262
  
263
  
264
  
265
  
266
  
267
  
268
  
269
  
270
  
271
  
272
  
273
  
274
  
275
  
276
  
277
  
278
  
279
  
280
  
281
  
282
  
283
  
284
  
285
  
286
  
287
  
288
  
289
  
290
  
291
  
292
  
293
  
294
  
295
  
296
  
297
  
298
  
299
  
300
  
301
  
302
  
303
  
304
  
305
  
306
  
307
  
308
  
309
  
310
  
311
  
312
  
313
  
314
  
315
  
316
  
317
  
318
  
319
  
320
  
321
  
322
  
323
 

四、运行结果

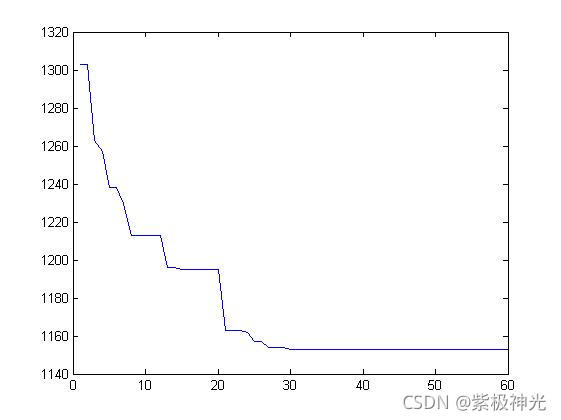
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/120289319