【优化算法】蚁狮优化算法(ALO)【含Matlab源码 1307期】
【摘要】
一、获取代码方式
获取代码方式1： 完整代码已上传我的资源：【优化算法】蚁狮优化算法(ALO)【含Matlab源码 1307期】
获取代码方式2： 通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，...
一、获取代码方式
获取代码方式1：
完整代码已上传我的资源：【优化算法】蚁狮优化算法(ALO)【含Matlab源码 1307期】
获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。
备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；
二、蚁狮优化算法简介
蚁狮算法是一种模仿自然界中蚁狮的捕猎机制的智能算法。蚁狮在沙子中，利用它的下颚挖出一个圆锥形的沙坑作为捕猎陷阱。一旦有猎物落陷阱，蚁狮便会将它拖入沙子底部并吃掉。通过与一些其他流行的智能算法比较，例如PSO、GA和杜鹃算法（CS),ALO显示出更好的收敛性、准确性和鲁棒性，但依然存在着收敛准确度低、易陷入局部最优解的缺陷。
(1）蚂蚁随机游走
首先假设由n个蚂蚁组成的蚂蚁种群Xant=(XA,1,XA,n,…,XA,N)T,XdA,n是第n个蚂蚁的第d个变量。蚂蚁移动的数学表达为
式中，XA,n(t)为迭代t次时第n个蚂蚁的位置；cums m为累积和；tm a x为最大迭代次数。
为防止个体越限，对其进行标准化处理，即
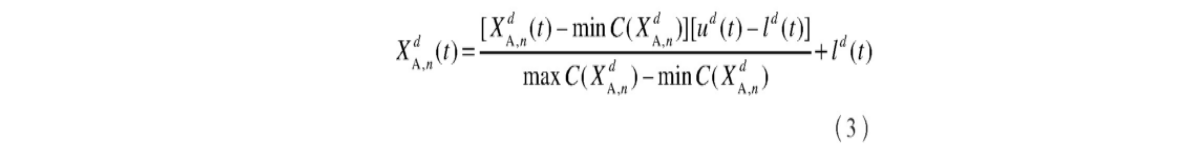
式中，min C(XdA,n)、max C(XdA,n)分别为第n只蚂蚁随机游走时的最小和最大步长；ud(t)、ld(t)分别为第t次迭代时第d个变量的上界和下界。
三、部分源代码
clear all
clc
SearchAgents_no=40; % Number of search agents
Function_name='F1'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper)
Max_iteration=500; % Maximum numbef of iterations
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,cg_curve]=ALO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
function [Elite_antlion_fitness,Elite_antlion_position,Convergence_curve]=ALO(N,Max_iter,lb,ub,dim,fobj)
% Initialize the positions of antlions and ants
antlion_position=initialization(N,dim,ub,lb);
ant_position=initialization(N,dim,ub,lb);
% Initialize variables to save the position of elite, sorted antlions,
% convergence curve, antlions fitness, and ants fitness
Sorted_antlions=zeros(N,dim);
Elite_antlion_position=zeros(1,dim);
Elite_antlion_fitness=inf;
Convergence_curve=zeros(1,Max_iter);
antlions_fitness=zeros(1,N);
ants_fitness=zeros(1,N);
% Calculate the fitness of initial antlions and sort them
for i=1:size(antlion_position,1)
antlions_fitness(1,i)=fobj(antlion_position(i,:));
end
[sorted_antlion_fitness,sorted_indexes]=sort(antlions_fitness);
for newindex=1:N
Sorted_antlions(newindex,:)=antlion_position(sorted_indexes(newindex),:);
end
Elite_antlion_position=Sorted_antlions(1,:);
Elite_antlion_fitness=sorted_antlion_fitness(1);
% Main loop start from the second iteration since the first iteration
% was dedicated to calculating the fitness of antlions
Current_iter=2;
while Current_iter<Max_iter+1
% This for loop simulate random walks
for i=1:size(ant_position,1)
% Select ant lions based on their fitness (the better anlion the higher chance of catching ant)
Rolette_index=RouletteWheelSelection(1./sorted_antlion_fitness);
if Rolette_index==-1
Rolette_index=1;
end
% RA is the random walk around the selected antlion by rolette wheel
RA=Random_walk_around_antlion(dim,Max_iter,lb,ub, Sorted_antlions(Rolette_index,:),Current_iter);
% RA is the random walk around the elite (best antlion so far)
[RE]=Random_walk_around_antlion(dim,Max_iter,lb,ub, Elite_antlion_position(1,:),Current_iter);
ant_position(i,:)= (RA(Current_iter,:)+RE(Current_iter,:))/2; % Equation (2.13) in the paper
end
for i=1:size(ant_position,1)
% Boundar checking (bring back the antlions of ants inside search
% space if they go beyoud the boundaries
Flag4ub=ant_position(i,:)>ub;
Flag4lb=ant_position(i,:)<lb;
ant_position(i,:)=(ant_position(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
ants_fitness(1,i)=fobj(ant_position(i,:));
end
function func_plot(func_name)
[lb,ub,dim,fobj]=Get_Functions_details(func_name);
switch func_name
case 'F1'
x=-100:2:100; y=x; %[-100,100]
case 'F2'
x=-100:2:100; y=x; %[-10,10]
case 'F3'
x=-100:2:100; y=x; %[-100,100]
case 'F4'
x=-100:2:100; y=x; %[-100,100]
case 'F5'
x=-200:2:200; y=x; %[-5,5]
case 'F6'
x=-100:2:100; y=x; %[-100,100]
case 'F7'
x=-1:0.03:1; y=x %[-1,1]
case 'F8'
x=-500:10:500;y=x; %[-500,500]
case 'F9'
x=-5:0.1:5; y=x; %[-5,5]
case 'F10'
x=-20:0.5:20; y=x;%[-500,500]
case 'F11'
x=-500:10:500; y=x;%[-0.5,0.5]
case 'F12'
x=-10:0.1:10; y=x;%[-pi,pi]
case 'F13'
x=-5:0.08:5; y=x;%[-3,1]
case 'F14'
x=-100:2:100; y=x;%[-100,100]
case 'F15'
x=-5:0.1:5; y=x;%[-5,5]
case 'F16'
x=-1:0.01:1; y=x;%[-5,5]
case 'F17'
x=-5:0.1:5; y=x;%[-5,5]
case 'F18'
x=-5:0.06:5; y=x;%[-5,5]
case 'F19'
x=-5:0.1:5; y=x;%[-5,5]
case 'F20'
x=-5:0.1:5; y=x;%[-5,5]
case 'F21'
x=-5:0.1:5; y=x;%[-5,5]
case 'F22'
x=-5:0.1:5; y=x;%[-5,5]
case 'F23'
x=-5:0.1:5; y=x;%[-5,5]
end
L=length(x);
f=[];
for i=1:L
for j=1:L
if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
f(i,j)=fobj([x(i),y(j)]);
end
if strcmp(func_name,'F15')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
if strcmp(func_name,'F19')==1
f(i,j)=fobj([x(i),y(j),0]);
end
if strcmp(func_name,'F20')==1
f(i,j)=fobj([x(i),y(j),0,0,0,0]);
end
if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
end
end
surfc(x,y,f,'LineStyle','none');
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
四、运行结果
五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。
原文链接：qq912100926.blog.csdn.net/article/details/120209117
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）