【气动学】基于matlab改进的遗传和粒子群算法高斯烟羽模型模拟气体扩散【含Matlab源码 1061期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【气动学】基于matlab改进的遗传和粒子群算法高斯烟羽模型模拟气体扩散【含Matlab源码 1061期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、高斯烟羽模型简介

1 高斯羽烟模型方程

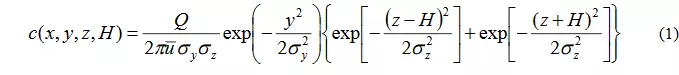
式中c为污染物浓度(单位：kg/m3)
Q为源强(单位：kg/s)
u为泄漏高度的平均风速(单位：m/s)
y、z分别用浓度标准偏差表示的y轴及z轴上的扩散参数
H为泄漏有效高度(单位：m)

2 扩散系数系数

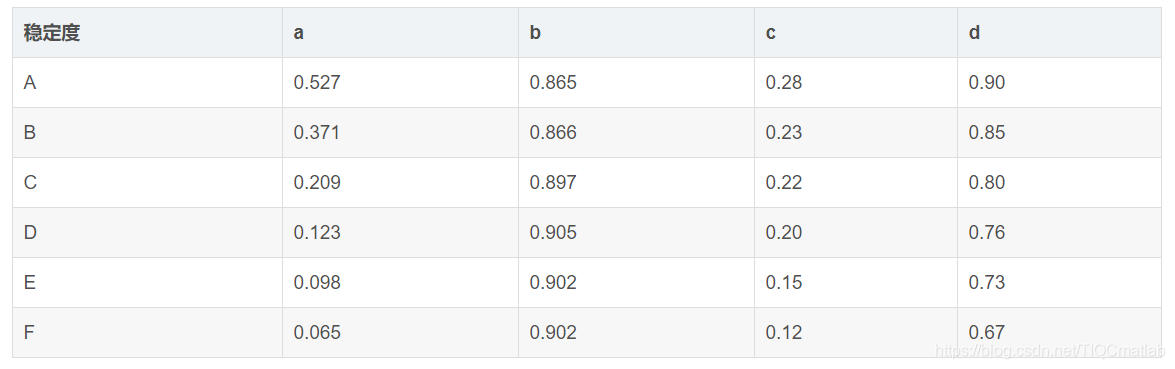
三、部分源代码

clc;clear;close all;
[xm1,xv1,a1] = mGA(100,2,1000,500,0);
[xm2,xv2,a2] = mPSO(1000,2,2,0.9,0.4,500,3);
[x_zuobiao,y_zuobiao]= gaosiyanyu(5,10,10000.5);
function [xm,xv,accuracy] = mGA(popsize,lenchrom,maxgen,popmax,popmin)
%-------------遗传算法解泄漏源点，效果最好
%% 输入参数
% popsize %种群规模
% lenchrom   %变量字串长度
% maxgen   % 进化次数  
% popmax % 种群最大值
% popmin   % 种群最小值
%% 输出参数
% xm 泄漏源坐标,针对泄漏源坐标，论文只考虑地面坐标即xm(1)=x和xm(2)=y
% xv泄漏源强估计值,主要检验方法的有效性
% accuracy方法精确度（%）
bound=[popmin popmax;popmin popmax];  %变量范围
%% 产生初始粒子和速度
for i=1:popsize
    %随机产生一个种群
    GApop(i,:)=Code(lenchrom,bound);       %随机产生个体
    %计算适应度
    fitvalue(i)=fitness(GApop(i,:));            %染色体的适应度
end

%找最好的染色体
[bestfitness,bestindex]=min(fitvalue);
xm=GApop(bestindex,:);   %全局最佳
gbest=GApop;                %个体最佳
fitnessgbest=fitvalue;       %个体最佳适应度值
xv=bestfitness;   %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
        %种群更新 GA选择更新
        GApop=Select(GApop,fitvalue,popsize); % 其中Select为选择算子函数

        % 交叉操作 GA
        pc=i/maxgen; % maxgen  进化次数  
        GApop=Cross(pc,lenchrom,GApop,popsize,bound); % 其中Cross为交叉算子函数

        % 变异操作 GA变异
        pm=i/maxgen;
        GApop=Mutation(pm,lenchrom,GApop,popsize,[i maxgen],bound);

        pop=GApop;
        
      for j=1:popsize
        %适应度值即变量约束条件
        if 1*pop(j,1)+0*pop(j,2)<=5000
            if (0*pop(j,1)+1*pop(j,2)<=200) && (0*pop(j,1)-1*pop(j,2)>=-200)
                    fitvalue(j)=fitness(pop(j,:));
            end
        end
        %个体最优更新
        if fitvalue(j) < fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitvalue(j);
        end
        
        %群体最优更新
        if fitvalue(j) < xv
            xm = pop(j,:);
            xv = fitvalue(j);
        end
      end
    
    yy(i)=xv;     
end

%% 作图分析
Q = 10000.5;%泄漏源强
accuracy = abs(Q-xv)/Q;
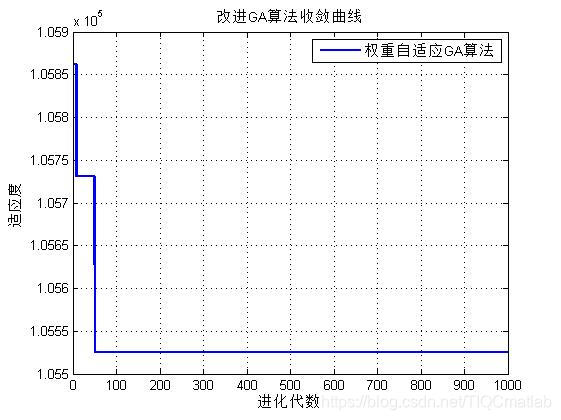
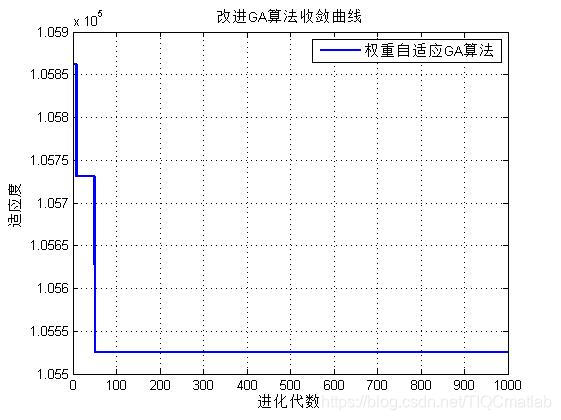
figure;plot(yy,'linewidth',2);hold on
xlabel('进化代数');ylabel('适应度');
title('改进GA算法收敛曲线');
legend('权重自适应GA算法')
grid on
[x,y,C] = point;
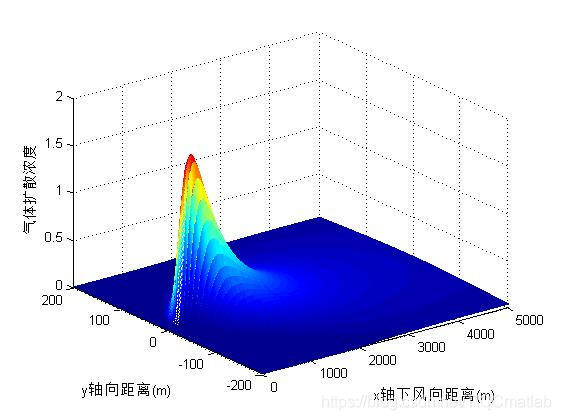
figure;mesh(x,y,C);
xlabel('x轴下风向距离(m)');ylabel('y轴向距离(m)');zlabel('气体扩散浓度')
figure;surf(x,y,0*C,C,'edgecolor','none','facecolor','interp');hold on;plot(xm(1),xm(2),'r.','MarkerSize',10)
xlabel('x轴下风向距离(m)');ylabel('y轴向距离(m)');
end

%% 检测函数
function V=fitness(v)
%% 输入参数
x = v(:,1); % 表示泄漏源的x值
y = v(:,2);  % 表示泄漏源的y值
%% 输出参数
% V 表示最佳适应度值，同时表示迭代过程中的泄露源强值
c = [112.3840,99.0546,51.0527,8.7177,19.9691,257.4304,...
    当然也可以只采用四个；
u = 5;% 风速
Hr = 10; %泄漏点有效高度
z = 0;%高度
Q = 10000.5;%泄漏源强

% 大气稳定度
A 
B1=0.16;B2=0.0001;B3=0.12;
C1=0.11;C2=0.0001;C3=0.08;C4=0.0002;
D1=0.08;D2=0.0001;D3=0.06;D4=0.0015;
E1=0.06;E2=0.0001;E3=0.03;E4=0.0003;
F1=0.04;F2=0.0001;F3=0.016;F4=0.0003;
% 选择大气稳定度
w = 'F'; % 如果w = 'A';就表示选择大气稳定度为A的情况进行研究，类似地，w = 'B';等。
switch w
% 大气稳定度
A1=0.22;A2=0.0001;A3=0.20;
B1=0.16;B2=0.0001;B3=0.12;
C1=0.11;C2=0.0001;C3=0.08;C4=0.0002;
D1=0.08;D2=0.0001;D3=0.06;D4=0.0015;
E1=0.06;E2=0.0001;E3=0.03;E4=0.0003;
F1=0.04;F2=0.0001;F3=0.016;F4=0.0003;
% 选择大气稳定度
w = F; % 如果w = 'A';就表示选择大气稳定度为A的情况进行研究，类似地，w = 'B';等。
switch w
    case 'A'
        
        Ty = ty1*x.*(1+ty2*x).^-0.5;%水平扩散系数
        Tz = tz1*x;%垂直扩散系数
    case 'B'
        ty1=B1;ty2=B2;tz1=B3;
        Ty = ty1*x.*(1+ty2*x).^-0.5;%水平扩散系数
        Tz = tz1*x;%垂直扩散系数
    case 'C'
        ty1=C1;ty2=C2;tz1=C3;tz2=C4;
        Ty = ty1*x.*(1+ty2*x).^-0.5;%水平扩散系数
        Tz = tz1*x.*(1+tz2*x).^-0.5;%垂直扩散系数
    case 'D'
        ty1=D1;ty2=D2;tz1=D3;tz2=D4;
        Ty = ty1*x.*(1+ty2*x).^-0.5;%水平扩散系数
        Tz = tz1*x.*(1+tz2*x).^-0.5;%垂直扩散系数
    case 'E'
        ty1=E1;ty2=E2;tz1=E3;tz2=E4;
        Ty = ty1*x.*(1+ty2*x).^-0.5;%水平扩散系数
        Tz = tz1*x.*(1+tz2*x).^-0.5;%垂直扩散系数
    case 'F'
        ty1=F1;ty2=F2;tz1=F3;tz2=F4;
        Ty = ty1*x.*(1+ty2*x).^-0.5;%水平扩散系数
        Tz = tz1*x.*(1+tz2*x).^-0.5;%垂直扩散系数
end
  %% 检测函数
function Q=fit(u1,hr,data,F)
%% 输入参数
x = data(:,2); % 表示泄漏源的x值
y = data(:,3);  % 表示泄漏源的y值
%% 输出参数
% V 表示最佳适应度值，同时表示迭代过程中的泄露源强值
% c = [112.3840,99.0546,51.0527,8.7177,19.9691,257.4304,...
%     53.4442,51.7675,43.7906,28.0270,34.9047,66.5592,...
%     27.5724,27.1807,25.2141,20.6378,22.8799]; % 监测到的浓度，我们用了17个，当然也可以只采用四个；
c=data(:,1);
u = u1;% 风速
Hr = hr; %泄漏点有效高度
z = 0;%高度

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
 

四、运行结果

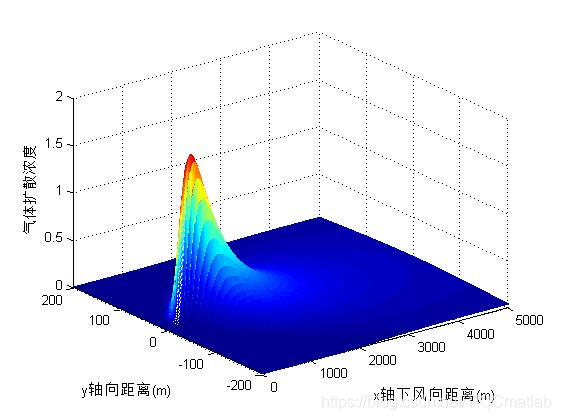
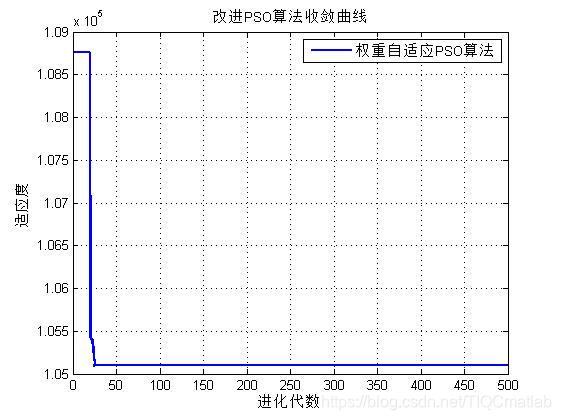
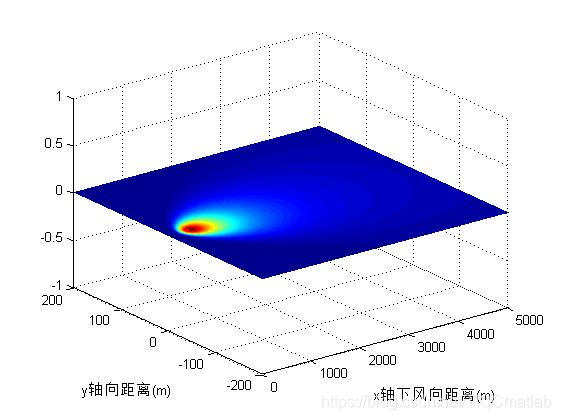
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 门云阁.MATLAB物理计算与可视化[M].清华大学出版社，2013.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/118269181